פנגייה

LSY1_EEQ Exam Example Questions

Question 1

Calculate

where and .

Solution:
The operation described here is the convolution of and :

By the sifting property, we know that:

Therefore, in our case:

Question 2

What’s the -norm of 𝟙?

Solution:
First, let’s rewrite the function in human readable math:

𝟙

The norm of this signal is:

because is a monotonically increasing function, it is largest at . Therefore:

Question 3

What’s the -norm of 𝟙?

Solution:
Rewriting:

𝟙

Therefore, the -norm of is unbounded:

Question 4

Is the continuous signal, that its spectrum is shown in the following figure, real? (Assume that is real).
book

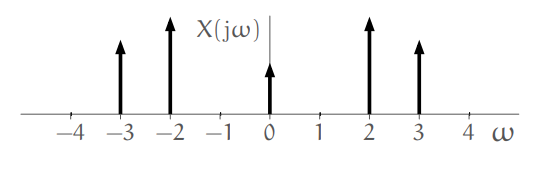
The relevant figure for questions 4, 5.

Solution:
Since the spectrum of the signal is symmetric and real, we can say that the signal itself is symmetric and real.

Question 5

Is the signal from the previous question periodic?

Solution:
The frequencies of a periodic signal are represented as impulses in its spectrum. So yes, the signal is periodic.

Question 6

Is the continuous signal, that its spectrum is shown in the following figure, real? (Assume that is real).

book

The relevant figure for questions 6, 7.

Solution:
The spectrum may be real, but it isn’t symmetric, meaning the the original signal isn’t real.

Question 7

Is the signal from the previous question periodic?

The frequencies of a periodic signal are represented as impulses in its spectrum. So no, the signal isn’t periodic.

Question 8

Four continuous signals and their (not corresponding) spectrums are shown in the following figure:
book

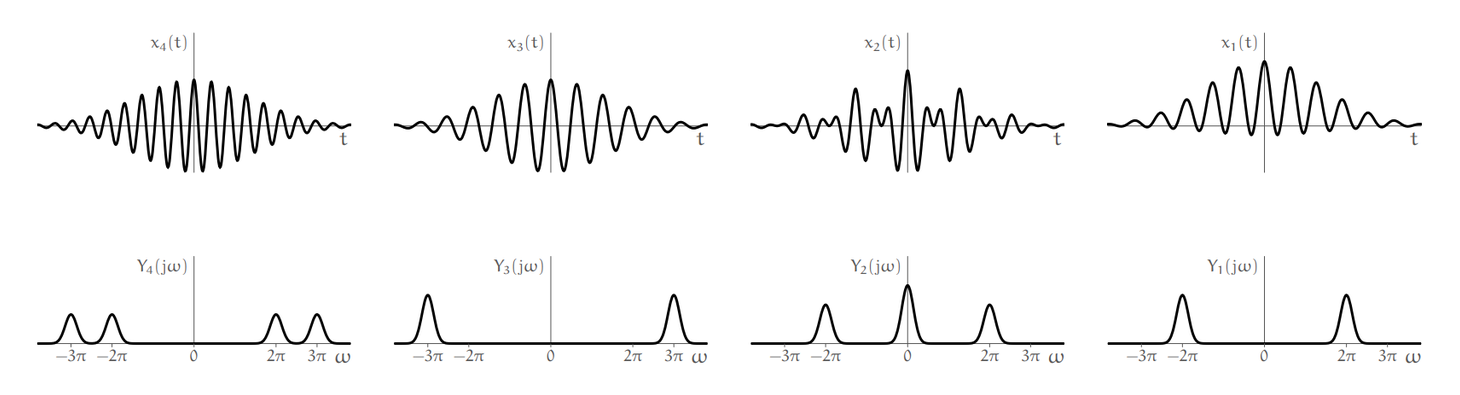
Signals in time and frequency domain

Match to .

Solution:
The signal is the only one that is offset from the center, meaning that one of its frequencies is . The only spectrum that matches that is :

The signal is the only signal that has two distinctly different frequencies, and the only spectrum that matches that is , as it has two frequencies - (counted as two because of symmetry):

We are left with and , with the only difference between them being that has a higher frequency than . Therefore:

Question 9

The spectrum of an analog signal is shown in the following figure:
book

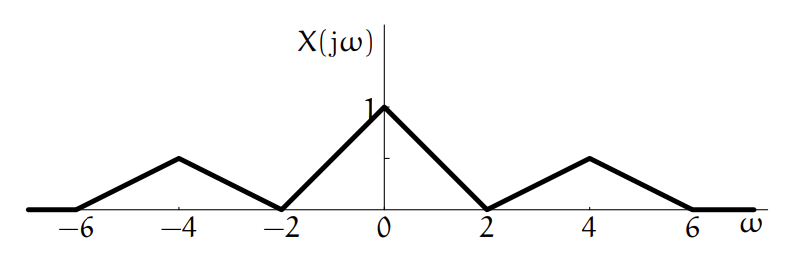
Spectrum of an analog signal.

Draw the spectrum of the sampled signal such that for sampling period .

Solution:
Because the sampling period is , the Nyquist frequency is:

which means we need to fold around :
bookhue

Spectrum of the corresponding sampled signal.

Question 10

The spectrum of an analog signal and its sampled signal are shown in the following figure:

book

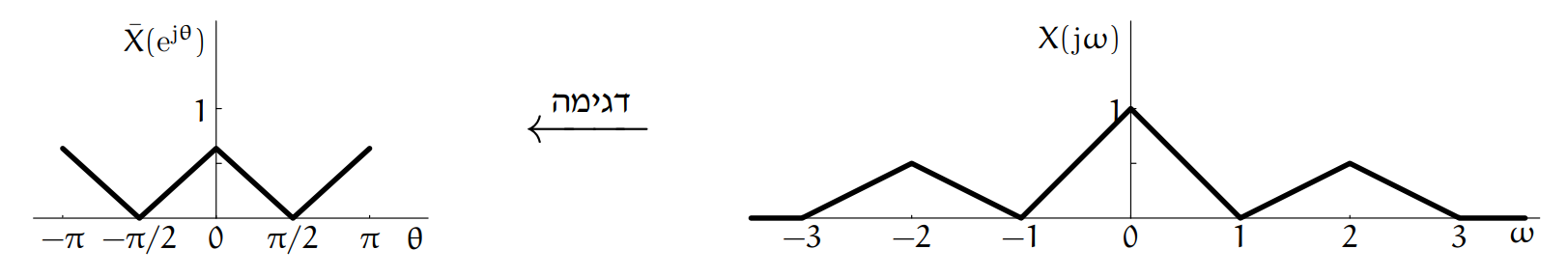
Spectrum of an analog signal and its sampled form.

Solution:
From the previous question, we know that the spectrum of the sampled signal is a result of the analog signal folding around . Therefore, this is its Nyquist frequency, which is given by:

Question 11

A discrete-time signal , with sample time , has been converted to an analog signal by zero-order hold:
book

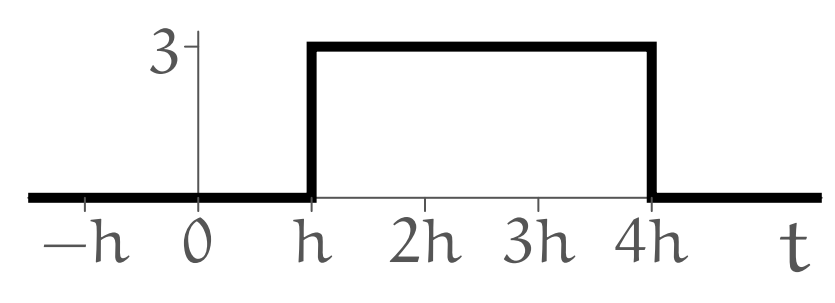
Analog signal .

What’s in terms of elementary signals (pulse, step…)?

Solution:
From the definition of zero-order hold we see that the discrete time signal is of the form:

The discrete-time signal .

From the figure:

Question 12

A discrete-time signal , with sample time , has been converted to an analog signal by -interpolator:

book

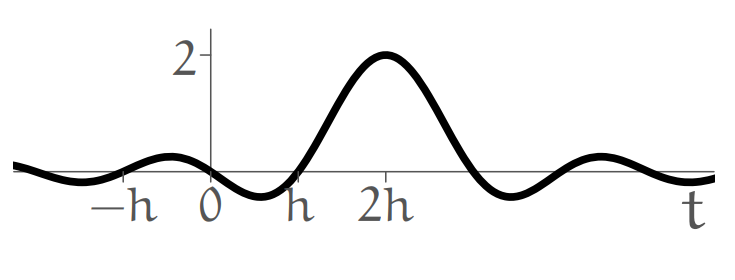
Analog signal .

What’s in terms of elementary signals (pulse, step…)?

Solution:
A pulse (delta function) going though a -interpolator yields a simple in the continuous-time domain (times ). Since our is shifted, the discrete-time signal is:

Question 13

Can the following graph be the spectrum of a discrete-time signal?
book

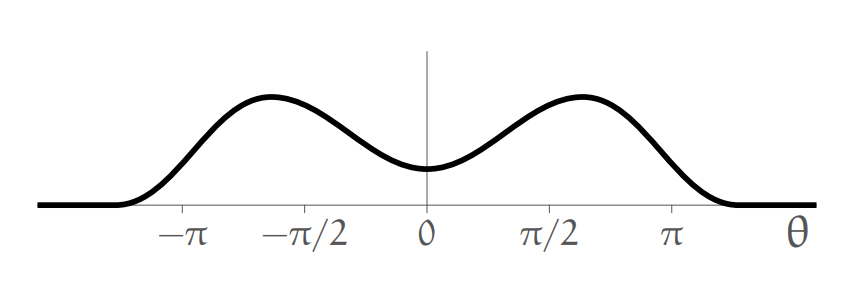
A general curve.

Solution:
No, its bounds aren’t (or at least periodic over ).

Question 14

Decompose the rational function

to partial fractions.

Solution:
Rewriting the function:

By partial fraction expansion:

Which is why:

Question 15

The function

Is the Laplace transform of with . Does its Fourier transform exist?

Solution:
We can think of Fourier transform as a special case of the Laplace transform - specifically on the imaginary axis. Since the Laplace transform doesn’t exist for (because its ), we conclude that the Fourier transform must not exist.

Question 16

Is the system such that static?

Solution:
Because depends on the value of the input only at time , it is static.

Question 17

Is the system such that linear?

Solution:
For :

Therefore, the system is linear.

Question 18

Is the system such that time-invariant?

Solution:
For :

Therefore, the system is time-variant.

Question 19

Is the system such that static?

Solution:
Because depends on the value of the input only at time , it is static.

Question 20

Is the system such that linear?

Solution:
For :

Therefore, the system is not linear.

Question 21

Is the system such that time-invariant?

Solution:
For :

Therefore, the system is time-invariant.

Question 22

Is a linear system such that static?

Solution:
In general, no, because of initial conditions . If depends on , we may get that depends on , which means it is not static.

Question 23

Is a system that its impulse response satisfies 𝟙 causal?

Solution:
A LTI system is causal iff , which is satisfied in our case. Therefore, the system is causal.

Question 24

Is a system that its impulse response satisfies 𝟙 BIBO stable?

Solution:
A LTI system is BIBO stable iff . In our case:

𝟙

Which by special integrals, we know isn’t bounded. Therefore, the system isn’t BIBO stable.

Question 25

Is a system that its impulse response satisfies 𝟙 causal?

Solution:
A LTI system is causal iff . In our case, is shifted by , which means the support isn’t completely in , therefore the system isn’t causal.

Question 26

Is a system that its impulse response satisfies 𝟙 BIBO stable?

Solution:
A LTI system is BIBO stable iff . In our case:

𝟙

Which by special integrals, we know is bounded. Therefore, the system is BIBO stable.

Question 27

What’s the transfer function of that is described by:

Solution:
Rearranging, we get:

Applying the Laplace transform to both sides of the equation, we get:

Question 28

What’s the transfer function of that is described by:

Solution:
Rearranging, we get:

Applying the z-transform to both sides of the equation, we get:

Question 29

What’s the impulse response of that is described by the equation:

Solution:
Substituting :

Question 30

What’s the transfer function of that is described by:

Solution:
Applying the Laplace transform to both sides of the equation, we get:

Question 31

Is the system with transfer function

stable and causal?

Solution:
The system isn’t proper, therefore it isn’t causal and stable.

Question 32

Is the system with transfer function

stable and causal?

Solution:
To check stability and causality, we can see that all the coefficients of the denominator are non-zero and have the same sign, which means it at least satisfies the necessary condition for stability. For the sufficient condition, we know that for a third-order polynomial we also need to check:

Since this is not true, we conclude that the system isn’t causal and stable.

Question 33

Is the system with transfer function

stable and causal?

Solution:
The only difference from the previous question is that we need to recheck the
the sufficient condition. We know that for a third-order polynomial need to make sure that:

Since this is true, we conclude that the system is causal and stable.

Question 34

Is the system with transfer function

causal?

Solution:
The system isn’t proper, therefore it isn’t causal.

Question 35

Is the system with transfer function

stable?

The single pole of this system is . Since it is inside the open unity circle, it is Schur, which means the system is stable.

Question 36

Is the system with transfer function

causal?

Solution:
The system is proper, therefore it is causal.

Question 37

Is the system with transfer function

stable?

Solution:
The poles of this system are:

Both of these poles are inside the open unit circle, which means the denominator is Schur, and the system is stable.

Question 38

Rearranging the function:

By first-order system transfer function:

Question 39

Rearranging the function:

By second-order system transfer function:

Question 40

What’s the overshoot and undershoot response for the following step response, in ?
book

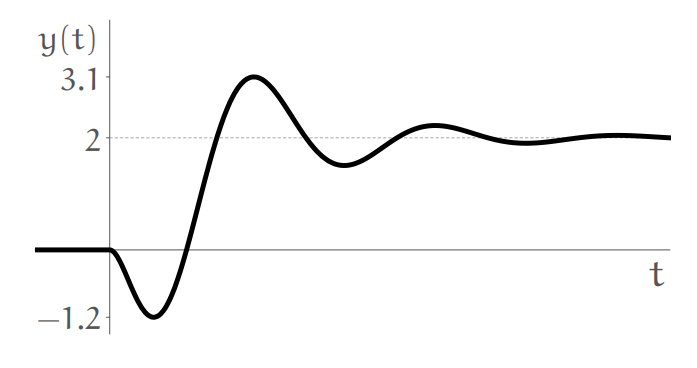
Step response.

Solution:
By definition:

Question 41

What’s the overshoot and undershoot response for the following step response, in ?

Solution:
book

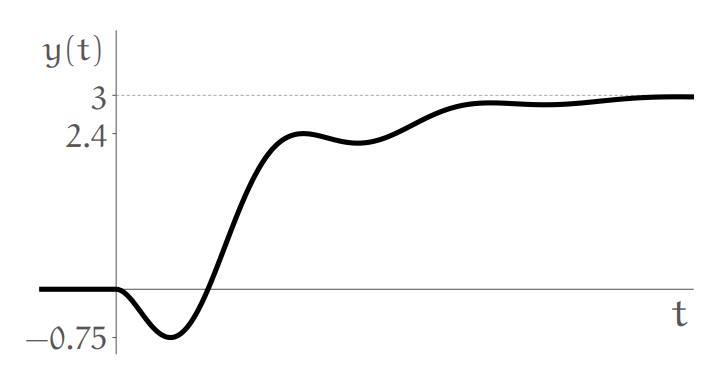
Step response.

By definition:

Question 42

Which of the two transfer functions and have a step response with a shorter rise time ?

Solution:
Rearranging :

The transient response is mainly shaped by . Because has a larger (), We conclude that has a longer rise time.

Question 43

Which of the following systems’ frequency response have a larger overshoot:

Solution:
From the standard forms we know that:

Because the only difference in the transient responses is , and we know that larger the the larger the overshoot, we conclude the has the larger overshoot.

Question 44

Draw the asymptotic magnitude curve of the frequency response of

Solution:
By Bode diagrams:
bookhue

The magnitude of the frequency response

Question 45

Given a linear system with the transform function and a Bode diagram:
book

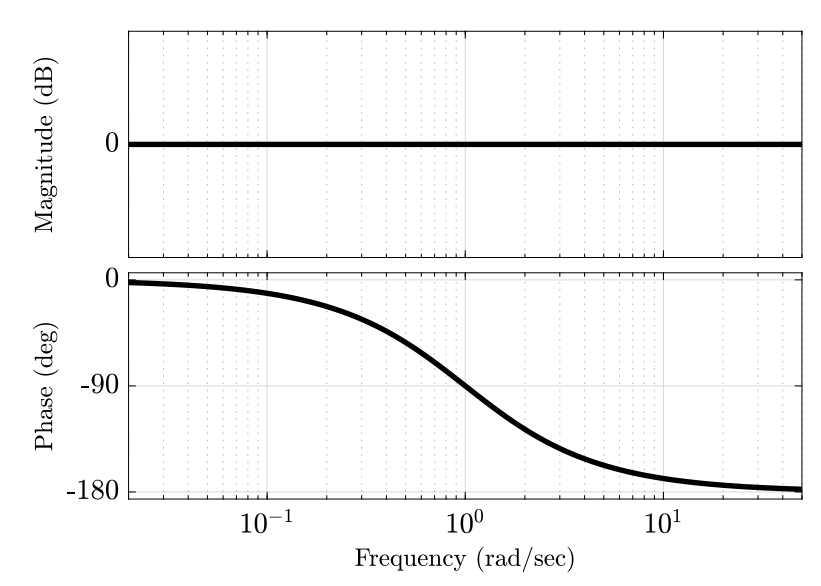
Bode diagram

Find and .

Solution:
We know that a zero in adds to the phase, and a pole in adds to the phase. From the constant magnitude we all conclude that corner frequencies of the nominator and the denominator are equal in magnitude. Therefore:

Question 46

Given a linear system with the transform function and a Bode diagram:

book

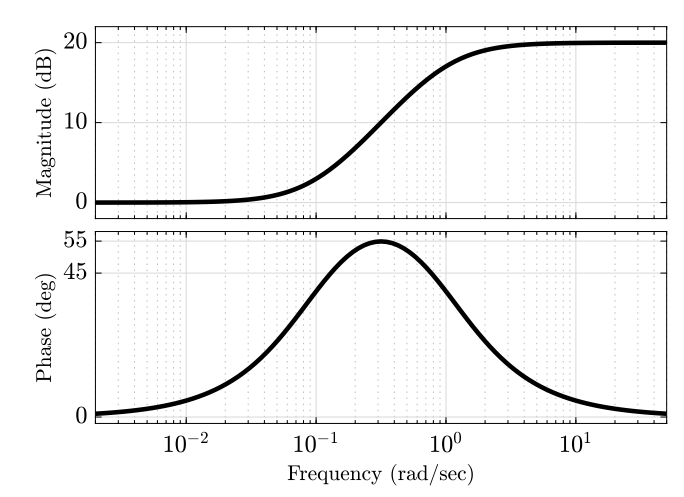
Bode diagram

Find .

Solution:
We know from the denominator about the corner frequency , which is also supposed to add a to the magnitude curve. That slope is mitigated by the corner frequency of the nominator, which we can guess is around , meaning .
We also know that a zero in adds to the phase, which means:

Question 47

Given a linear system with the transform function and a Bode diagram:

book

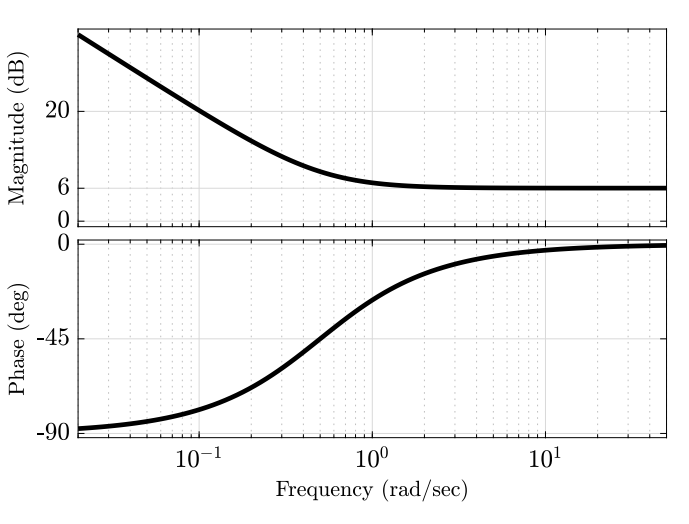
Bode diagram

Find and

Solution:
We see from the diagram that it begins with a downward slope. The only system that begins with such a slope is , meaning that . We are left with:

Since there is a corner frequency at (the graph passes at that point), we can conclude that . Because are added to the phase, we know that the zero is in . Therefore:

Question 48

In the following figure are 3 Bode diagrams and 3 polar diagrams. Match them.
book

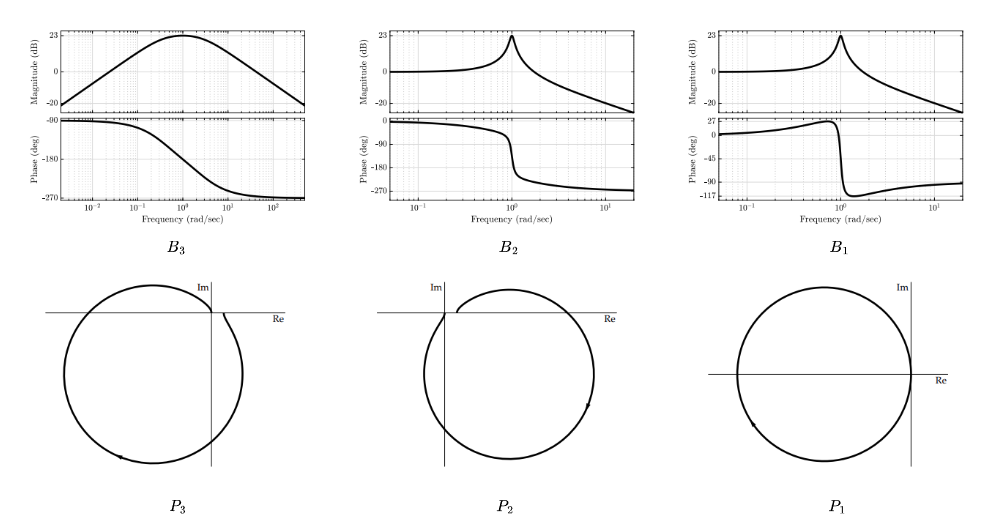
Bode and polar diagrams.

Solution:
We can match the figures by only looking at the phase diagrams of the Bode diagrams. begins positive, and then goes to the negative portion around . The only polar diagram that matches that is . is always negative, hence , which always has a negative to it (if you consider negative), is the matching one. We are left with and , that also match because they both begin at :

Question 49

In the following figure are represented an input an output signal of a system - :
book

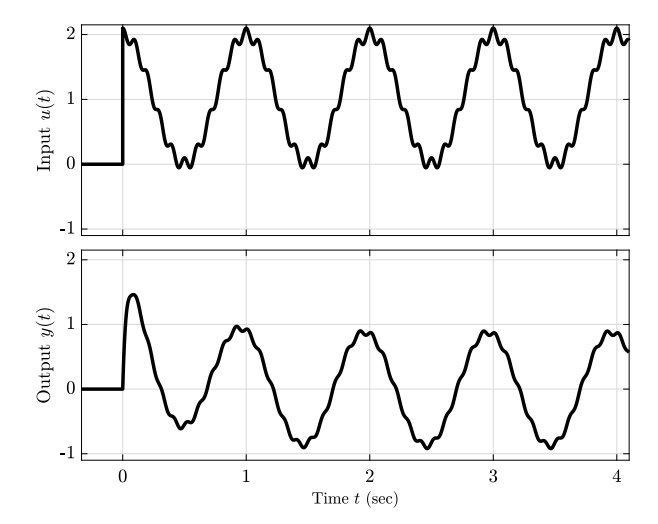
Signals .

Match the correct Bode diagram:
book

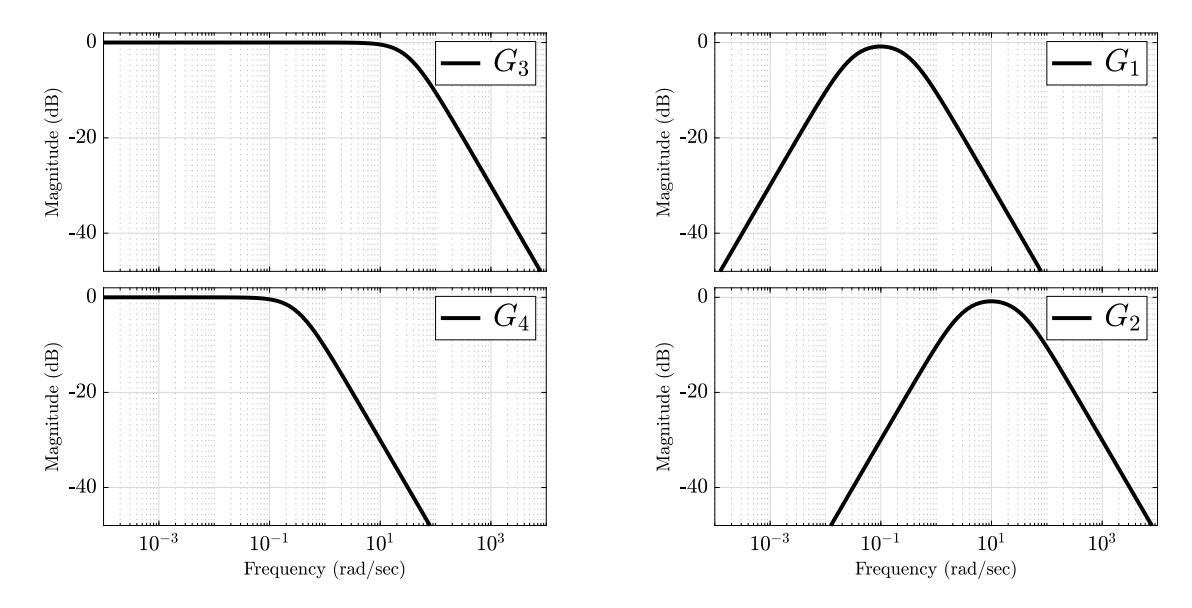
Bode diagrams .

Solution:
The static magnitude of the input is , while in the output it zeros out - , meaning the system has filtered that frequency out. The only graphs that filter out are and .

We also see that the high frequencies in the input have been filtered out, yes the the slower frequency, with , stays.
The corresponding frequency of that is , and the only graph that doesn’t completely filter it out is .

Question 50

The following graph is a polar description of a linear, time-invariant, and stable system. Its steady-state response to the input for a general is . Find and .

book

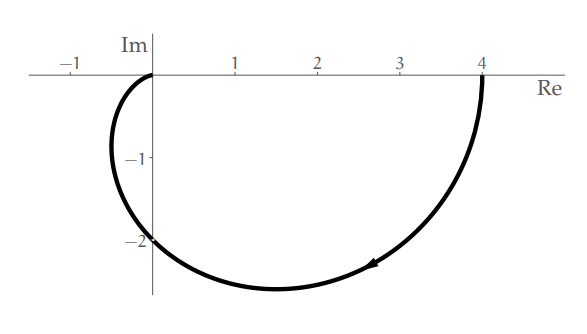
Polar description of a linear system.

Solution:
The input can be decomposed to two different signals:

The steady-state step response is simply (because the system is stable):

For the frequency input we know that the steady-state frequency response is:

In our case, and because the input is a . Substituting:

Therefore, the total steady-state response is:

Also, we know that the steady-state response is of the form:

Meaning:

From here I don’t really know how to explain. I want to thank from the deepness of my heart to the course instructors that provide clear and coherent explanations to what the fuck is going on with this course.

Question 51

Given the Routh table of the polynomial :

You can't use 'macro parameter character #' in math mode\begin{array}{c|ccc} 0 & 1 & 4 & 6 \\ 1 & 4 & 8 \\ 2 & 2 & 6 \\ 3 & -4 & 0 \\ 4 & 6 \end{array} $$How many roots of $D(s)$ are in $\mathbb{C}\setminus \bar{\mathbb{C}}_{0}$, and how many are in $\mathbb{C}_{0}$? **Solution**: According to [[LSY1_007 Laplace Transform#necessary-and-sufficient-condition-for-stability|necessary condition for stability]], since there are two signs changes, there are two roots in $\mathbb{C}_{0}$, and two roots in $\mathbb{C}\setminus \bar{\mathbb{C}}_{0}$. ## Question 52 Given the Jury table of the polynomial $D(z)=z^{3}+3z^{2}+6z+2$:

\begin{array}{c|ccc}
0 & 1 & 3 & 6 & 2 \
& 2 & 6 & 3 & 1 \
1 & -3 & -9 & 0 \
& 0 & -9 & -3 \
2 & -3 & -9 \
& -9 & -3 \
3 & 24
\end{array}
$$How many roots of are in , and how many are in ?

Solution:
Don’t know, don’t wanna know.

Question 53

Is for

Solution:
First, we need to find the characteristic equation of :

By Cayley–Hamilton we know that satisfies its own characteristic equation, meaning:

Question 54

Is it possible that:

Solution:
By definition:

We can see that the lower left expression will never amount to zero, therefore the statement isn’t correct.

Question 55

Calculate

By definition:

Question 56

Are the following two system realizations similar?

Solution:
The matrices in the those realizations don’t have the same eigenvalues, therefore they aren’t similar, which means the systems aren’t similar.

Question 57

Are the following two system realizations similar?

Solution:
The matrices in the those realizations have the same eigenvalues:

But, the Identity matrix is similar only to itself, therefore isn’t similar to , which means the system aren’t similar.

Question 58

Prove that is the solution of for initial condition .

Solution:
Substituting the solution:

Making sure the initial condition is satisfied:

Question 59

What’s the observer realization of the transfer function ?

Solution:
By canonical realization:

Question 60

What are the equilibrium points of the system ?

Solution:
The equilibrium points are where . In our case, , therefore:

Therefore the equilibrium point is .

Question 61

An autonomous response of a second order linear system is shown in the following figure:
book

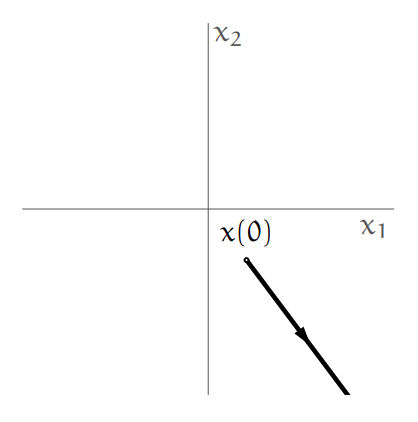
Autonomous response of the system.

Is the equilibrium point of the system asymptotically stable?

Solution:
No, we see from the figure that for that initial condition, the state of the system diverges, which means the system isn’t stable.

Question 62

An autonomous response of a second order linear system is shown in the following figure:

book

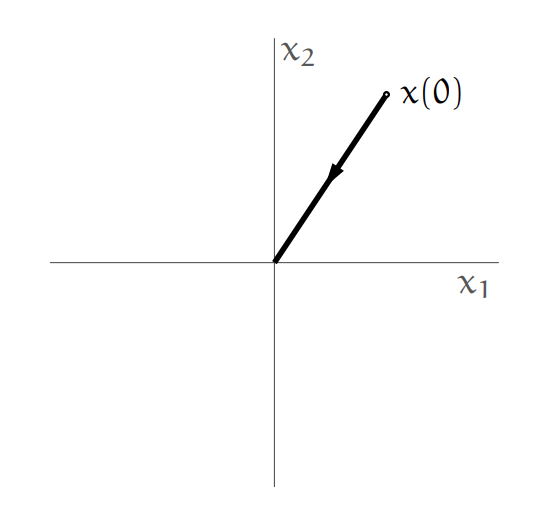
Autonomous response of the system.

Is the equilibrium point of the system asymptotically stable?

Solution:
For a second-oder system to be asymptotically stable, we need both of the eigenvalues to be negative. From the figure we see that at least one of the eigenvalues is negative, and thus any point on its eigenvector converges to zero. But, we still don’t know anything about the second eigenvalue, which might be positive. Therefore, we can’t say whether the system is stable or not.

Question 63

An autonomous response of a second order linear system is shown in the following figure:

book

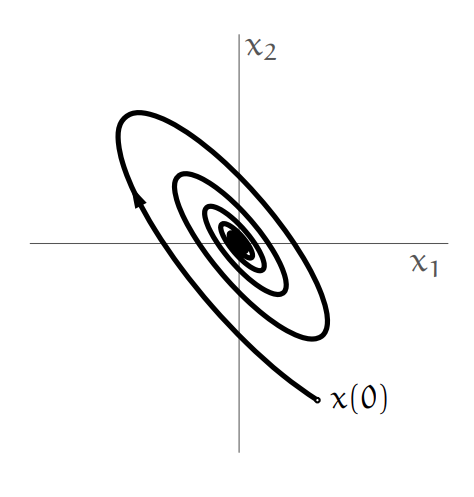
Autonomous response of the system.

Is the equilibrium point of the system asymptotically stable?

Solution:
Yes, we can see from the figure that there exists a circle around the equilibrium point where the system converges to the equilibrium point, which means the system is asymptotically stable.

Question 64

An autonomous response of a second order linear system is shown in the following figure:

book

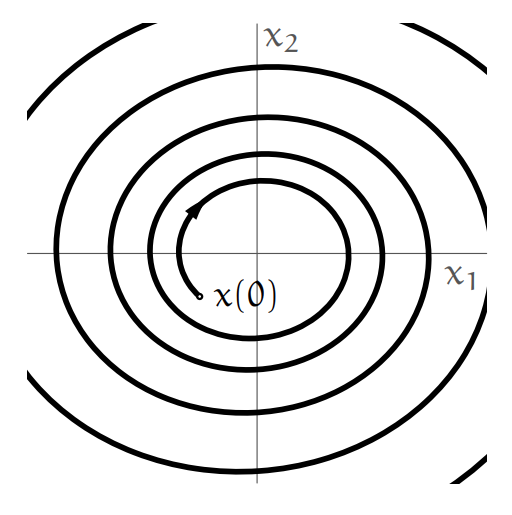
Autonomous response of the system.

Is the equilibrium point of the system asymptotically stable?

Solution:
No, the system clearly diverges from the initial condition outwards.

Question 65

What’s the equilibrium point of ?

Solution:
We simply need to find where :

Therefore:

Question 66

What’s the equilibrium point of ?

Solution:

Therefore:

Question 67

Given a nonlinear system:

Linearize it around the equilibrium point and find the transfer function of the linearized system .

Solution:
Derivatives:

Therefore, the linearized system is (where and ):

To find the transfer function, we substitute the second equation into the first one:

Therefore the transfer function is:

Question 68

Is the equilibrium point of the autonomous system Lyapunov stable?

Solution:
Both of the eigenvalues of the system ( and ) are negative, meaning that the system is Lyapunov stable.

Question 69

Is the equilibrium point of the autonomous system Lyapunov stable?

Solution:
Both of the eigenvalues of the system ( and ) satisfy , meaning that the system is Lyapunov stable.

Question 70

Given the linearization of a non-linear system around an equilibrium point , is a Lyapunov stable equilibrium point of ?

Solution:
By Lyapunov’s indirect method, if both of the eigenvalues of the linearized system are on the open left half plane (which is true in our case), than the non-linear system is asymptotically stable, and thus Lyapunov stable, around the equilibrium point.

Question 71

Given the linearization of a non-linear system around an equilibrium point , is a Lyapunov stable equilibrium point of ?

Solution:
By Lyapunov’s indirect method, If the rightmost eigenvalue of the Jacobian matrix is on the imaginary axis, then the stability conclusion is ambiguous. Therefore, we don’t know.