פנגייה

LSY1_010 Discrete-Time System Analysis

Introduction

From (Lathi & Green, 2018):
The counterpart of the Laplace transform for discrete-time systems is the -transform. The Laplace transform converts integro-differential equations into algebraic equations. In the same way, the z-transforms changes difference equations into algebraic equations, thereby simplifying the analysis of discrete-time systems.

The behavior of discrete-time systems is similar to that of continuous-time systems (with some differences). The frequency-domain analysis of discrete-time systems is based on the fact that the response of a linear, time-invariant, discrete-time (LTID) system to an everlasting exponential is the same exponential (within a multiplicative constant) given by . We then express an input as a sum of (everlasting) exponentials of the form .The system response to is then found as a sum of the system’s responses to all these exponential components. The tool that allows us to represent an arbitrary input as a sum of (everlasting) exponentials of the form is the -transform.

The -Transform

We define , the direct -transform of as:

where is a complex variable (). The signal , which is the inverse -transform of , can be obtained from by using the following inverse -transformation:

Symbolically:

Note that

Region of Convergence (ROC)

Definition:

The region of convergence, also called the region of existence, for the the -transform , is the set of values of (the region in the complex plane) for which the sum converges.

Final and Initial Values Theorems

Theorem:

Given a discrete signal with , the initial and final value theorems are as follows:

  1. Initial value theorem:

assuming exists.
2. Final value theorem:

assuming is converging.

Causality and Stability

Theorem:

If the transfer function of a DLTI system is rational, then

  • is causal iff is proper and
  • is -stable iff has no poles in .

Example:

The system is non-proper. Hence is not causal, but it is stable.

Jury table

Attention:

For the exam, we won’t need to use the Jury table approach. Christian has instead provided the Bilinear Transformation in the cheat sheet, since it is a much nicer to work with Routh table.

Definition:

Given the polynomial , the associated Jury table is

where for each :

(the -th row has elements). The Jury is said to be:

  • regular if all , and
  • singular otherwise.

Necessary and Sufficient Condition for Stability

Theorem:

Consider a polynomial in with :

  • is Schur iff the associated Jury table is regular and all the elements of the first column are positive.
  • If the Jury table is regular, then has no roots on the unit circle and the number of poles outside of the unit circle equals the number of negative elements in the first column of the table.
  • If the Jury table is singular, then is not Schur. Is this case, we cannot say anything about the location of the poles, except that there is at least one pole in .

Bilinear Transformation

Theorem:

The transformation enables to use the transform continuous system for the analysis of the discrete time system, such that:

  1. for a given transfer function , is a root of iff is a root of .
  2. is Schur iff is Hurwitz.

This transformation basically means:

i.e:
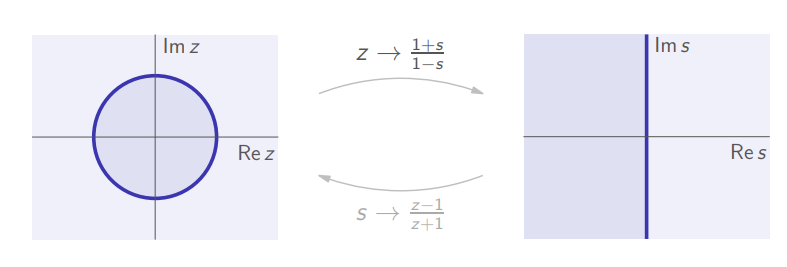
bookhue

Demonstration of the Bilinear transformation.