LSY1_006 Lyapunov Stability

Lyapunov Stability

Autonomous System

Definition:

A system of ODE’s which does not explicitly depend on the independent variable is called an autonomous system.

In the case of linear state-space equation, we get:

which is the state equation with zero inputs. It is also known as the unforced motion (or autonomous motion) of the system, where the state responds only to initial conditions.

the unforced motion fully represents properties of the system, while being easier to analyze.

Stability of Autonomous System

Definition:

Consider the following autonomous CLTV system:

An equilibrium of this system is said to be:

• Lyapunov stable if for every there is such that if , then:
  • asymptotically stable if it is Lyapunov stable and there is such that if , then:

Conceptually, the meanings of the above terms are the following:

• Lyapunov stability of an equilibrium means that solutions starting “close enough” to the equilibrium (within a distance  from it) remain “close enough” forever (within a distance  from it). Note that this must be true for any  that one may want to choose.

2. Asymptotic stability means that solutions that start close enough not only remain close enough but also eventually converge to the equilibrium.

The region of attraction of an asymptotically stable equilibrium is the set of initial conditions that generate states converging to . If the region of attraction is the whole , then the equilibrium is said to be globally asymptotically stable.

Stability for Linear State Space Models

Theorem:

An equilibrium of the autonomous linear system is

• Lyapunov stable iff its spectral radius is non-positive:

\rho(A)\in { s \in \mathbb{C}\mid\mathrm{Re}(s)\leq 0 }

\rho(A)\in { s \in \mathbb{C}\mid\mathrm{Re}(s)< 0 }

Lyapunov’s indirect method

Theorem:

Let for a continuously differentiable , be its equilibrium, and be the corresponding Jacobian matrix.

• If (all eigenvalues of are in the the open left half-plane - OLHP), then is asymptotically stable.
• If has at least one eigenvalue in , then is unstable.

If the rightmost eigenvalue of the Jacobian matrix is on the imaginary axis, then the stability conclusion is ambiguous.

Modal decomposition

A common way to analyze initial conditions for a given linear autonomous system is modal decomposition.

Consider the autonomous state equation

and assume that is diagonalizable with real eigenvalues. The solution is:

Denoting the eigenvectors and their inverse , i.e:

we can write:

Defining , we get

where the initial condition only affect the constant scalar coefficients .

The form

means that solutions to autonomous systems are a superposition of elementary exponential signals , each one of which is shaped by the corresponding eigenvectors, .
The signal is known as the th mode of the system, and the scalar is called the degree of excitation of the th mode by .

Exercises

Question 1

Consider the following state space equation:

Part a

Is the system Lyapunov stable?

Solution:
First, we’ll find the eigenvalues:

Therefore, , which means by its definition that the system is unstable.

Part b

Find a transformation diagonalizing the matrix .

Solution:
The eigenvectors:

• for : we get
• for : we get

Therefore:

Part c

Carry out the modal decomposition of the system with respect to any initial condition .

Solution:
The Modal decomposition is given by:

where

Part d

Find the response for the following two initial conditions. Draw the responses in a phase portrait.

Solution:
The inverse of :

• for , we get: Therefore, the response is:
• for , we get: Therefore, the response is:

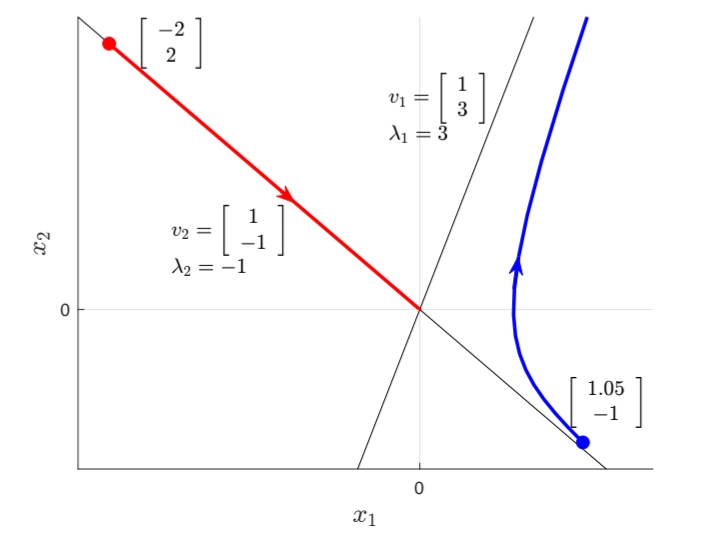
Phase portrait for both initial conditions

Question 2

Given the autonomous dynamics

Is their equilibria Lyapunov stable? Carry out the modal decompositions of the responses.

Solution:
Because the matrix is triangular, its eigenvalues are on the main diagonal:

Both the eigenvalues are on the open left half plane, therefore every equilibrium of this unforced dynamics is asymptotically stable.

For the modal decomposition, we need to find the corresponding eigenvectors.

• for : we get .
• for : we get .

The similarity transform is then:

its inverse:

Hence, the the degrees of excitations are given by:

And the modal decomposition:

In conclusion:

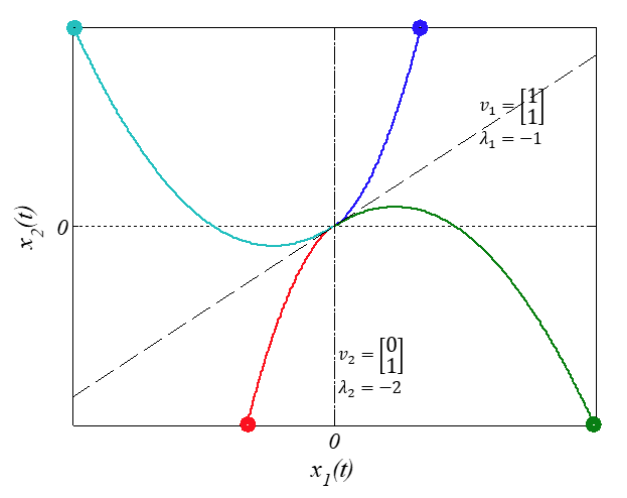
Phase portrait for initial conditions

There are 2 modes in this system, and , with faster than . Therefore, the exponent tends to faster than the exponent .

Question 3

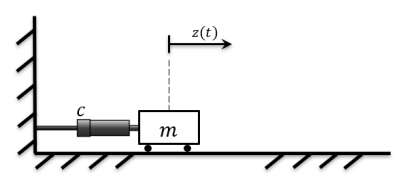
Mass damper system

The system is a mass damper system without a spring. The parameter values are . Also, the state variables are defined

Is the system stable? Find the response of the system to the initial conditions via the modes.

Solution:
It can be seen that the equation of motion of the system is

normalized:

Its physical realization is given by:

since and , we get:

The eigenvalues of are simply:

We have a linear system, which is why we can deduce that it is Lyapunov stable, but not asymptotically stable.

The eigenvectors are:

• for : we get .
• for : we get .

The similarity transform is then:

Its inverse:

Hence, the the degrees of excitations are given by (given ):

and the modal decomposition:

In conclusion:

It can be seen that the stable mode, , decays along the vector but the mode does not decay.

In general, when the system has modes with a real part 0, whose algebraic multiplicity is equal to the multiplicity geometrically, we will get a stable (non-asymptotic) system, i.e. a system that does not diverge from some initial condition but also does not converge.
It is important to understand that a system of this type is “stable” only for the reaction of initial conditions, and when the system will receive any input (even if it is bounded), it can diverge.

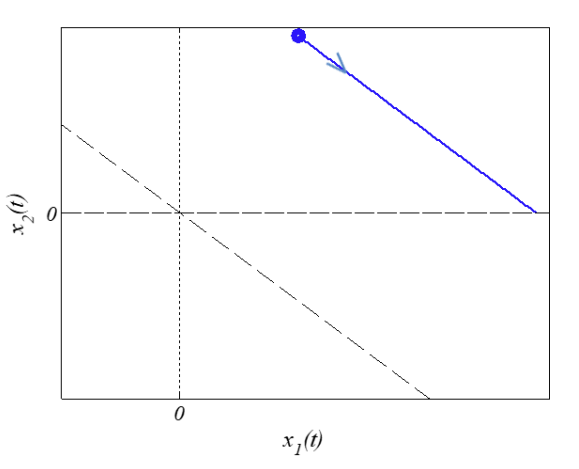
Phase portrait for a single initial condition

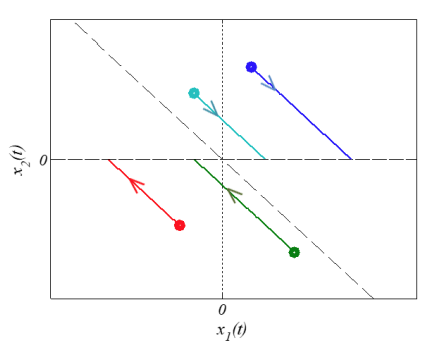
Phase portrait for both many initial conditions