LSY1_003 Classification of Systems

Causality

All state-space systems introduced so far (both LTV and LTI) have the property that the output before some time does not depend on the input after . Such systems are called causal.

Definition:

The state-space system (CLTV) is causal in the sense that given any two input signal and that

for some time , if then there exists an output such that and

Causality: For two inputs and that are equal to each other up to some , there must exist two outputs that are also equal to each other up to the same time .

Any practical system that operates in real time must necessarily be causal. We do not yet know how to build a system that can respond to future inputs. A noncausal system is prphetic system that knows the future input and acts on it in the present. Thus, if we apply an input starting at to a noncausal system, the output would begin even before .

The foregoing discussion may suggest that noncausal systems have no practical purpose. This is not the case; they are valuable in the study of systems for several reasons. Noncausal systems are realizable when the independent variable is other than “time” (e.g., space). Consider, for example, an electric field that is present at every point on the axis from to . In this case the input (i.e., the charge density ) starts at , but its output (the electric field ) begins before . Clearly, this space-charge system is noncausal.

Time Invariance

A key difference between the LTV and LTI systems introduced so far is that the latter have the property that time shifting of their inputs results in the time shifting of the output. This property justifies the terminology time-varying versus time-invariant for these systems.

Definition:

The state-space system (CLTI) is time-invariant in the sense that given any two input signals and such that:

for some time , if then there exists an output such that and

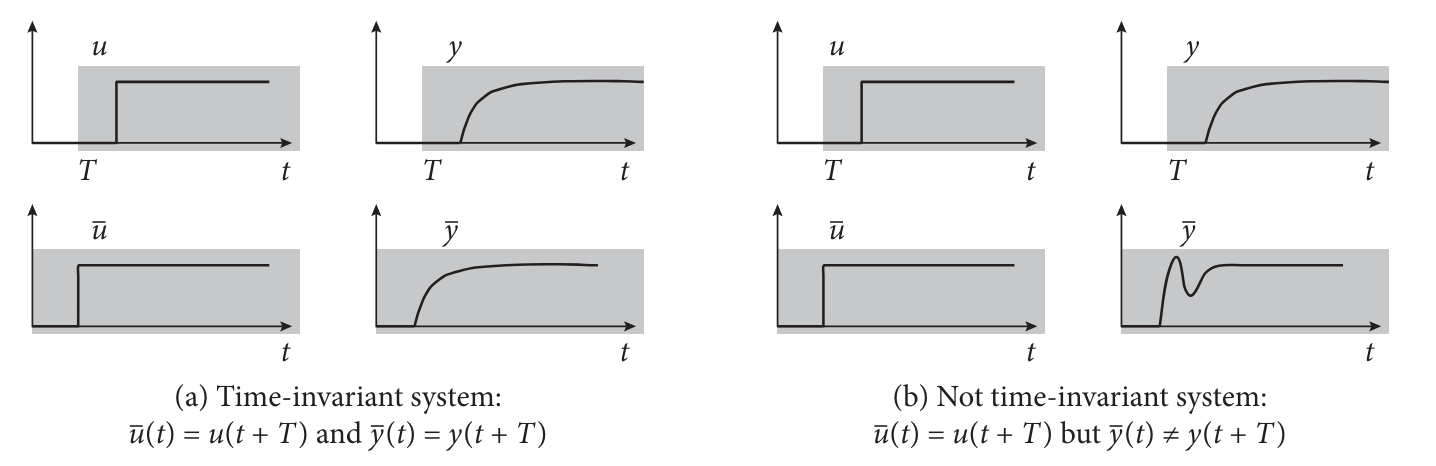
Time invariance: For an input with output , for every time shifted version of there must exist an output that is a time shifted version .

Linearity

Both the LTV and LTI system have the property that they can be viewed as linear maps from their inputs to appropriate outputs. This justifies the qualifier linear in LTV and LTI.

Definition:

The state-space system (CLTV) is linear in the sense that given any two input signals and and scalars , if and , then .

Example: Lineary of Constant-Coefficient Linear Differential Equations

Show that the system descrined the equation

is linear.
Solution:
Let the system response to the inputs and be and , reprectively. Then

Multiplying the first equation by , the second by , and adding them yield

But this equation is the system equation with

Thereforce, the system is linear.

Instanteneous and Dynamic Systems

A system’s output at any instant generally depends on the entire past inputs. However, in a special class of systems, the output at any instant depends only on its input at that instant. Such systems are said to be instantenous, static or memoryless systems. Otherwise, the system is said to be dynamic. A system whose response at is completely determined by the input signals over the past seconds is a finite-memory system with a memory of seconds.

Example: Assessing System Memory

Determine whether the following systems are memoryless:
1.

Solution:

1. in this case, the output at time is just twice the input at the same time . Since the output at a particular time depends only on the strength of the input at the same time, the system is memoryless.
2. Although it appears that the output at time depends on the input at the same time , we know that the slope (derivative) of cannot be determined solely from a single point. There must be some memory, even if infinitesimally small, involved. This is confirmed by using the funamental theorem of calculus to express the system as

Since the output at a particular time depends on more than just the input at the same time, the system is not memoryless.
3. The output at time is just the input at the same time multiplied by the coefficient . Since the output at a particular time depends only on the strength of the input at the same time, the system is memoryless.

Stable and Unstable Systems

Systems can also be classified as stable or unstable systems.

Definition:

A continuous-time system is said to be -stable if there are such that

for and .
-stability implies that for all .

Notes:

For the signals, stands for their norms.

If every bounded input applied at the input terminal results in a bounded output, the system is said to be stable externally. External stability can be ascertained by measurements at the external terminals (inputs and output) of the system. This type of stability is also known as -stability, or the stability in the BIBO (bounded-input/bounded-output) sense.

For linear systems, we can always take . i.e., a linear system is -stable if

Example:

Showing that a system is stable might not be easy. But in some cases it is:
If (A delay system), while , then

and

Thus, with a constant is both and -stable.

Example:

Showing that a system is unstable may be easier. One “just” needs to dream up a destabilizing input.
If , then

Because , the integrator is not BIBO stable.

Induced Norm

Definition:

Let be a stable CLTI system. The smallest for which the inequality above holds true is called the -induced norm of :

Example: with constant from the previous example, the induced norm is:

Exercises

Question 1

Classify the models below in terms of linearity, time invariance, (except the systems in items and ) causality.

1. 
   Linear, but not time invariant:
2. 
   Non-linear: for Time invariant.
3. 
   Linear, time invariant and not causal:
   The signal at time depends on at time .
4. 
   Non-linear: for time invariant and causal.
5. 
   Linear, time invariant, and causal.
6. 
   Linear, time invariant, and causal.