FLD1_E2023WB 2023 חורף מועד ב'

שאלה 1

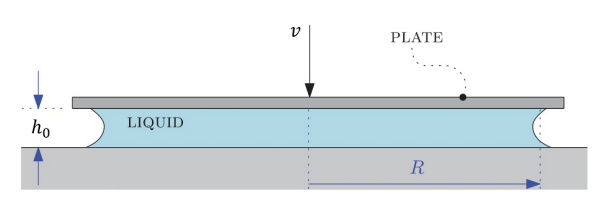
סכימת שתי הדסקות

סעיף א’

כדי להניח לובריקציה, עלינו לדרוש צמיגות דומיננטית - , וגם גאומטריה תמירה - . לרוב נזניח גם כוחות גוף, כך ש- .

סעיף ב’

נבחר נפח בקרה משתנה בזמן - גבולותיו העליונים צמודים לדסקות, וגודל רדיוסו הוא , ונשאר קבוע.

בחירת הנפח בקרה ומערכת הצירים

לפי שימור מסה אינטגרלי:

מאחר ו- קבוע, נישאר עם:

נחשב כל ביטוי בנפרד:

• שינוי הנפח בזמן:
  נפח הבקרה שלנו הוא גליל ברדיוס וגובה משתנה . לכן: נתון כי קצב שינוי הגובה הוא , ושהדסקות מתקרבות אחת לשנייה. לכן
• שינויים בספיקה הנפחית :
  קצב הזורם בגבול העליון והתחתון הוא , אבל גם הגבולות זזים בקצב זה, כך ש- בגבולות אלו. נסמן את קצב הזורם בגבול האופקי ב- (נתון כי הוא לא תלוי ב-) ונקבל כי:

נציב בחזרה בשימור מסה:

אם נתחשב גם בתנאי ההתחלה , נוכל לרשום , ואז:

סעיף ג’

מתח פנים לא בחומר.

שאלה 2

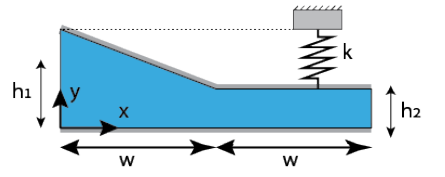
גיאומטריית הבעיה

סעיף א’

כדי שנהיה בגבול האינרציאלי, עלינו לדרוש ש- . במקרה המתואר:

את המהירות האופיינית נוכל למצוא מהספיקה הנתונה :

זו מהירות אופיינית, אז נוכל להניח פרופיל מהירות אחיד (אכפת לנו רק מסדר גודל , לא צריך עכשיו להיכנס לפרטי פרטים):

נציב בחזרה בתנאי על ריינולדס המוקטן:

סעיף ב’

נבחר קו זרם בתעלה:

שתי נקודות על אותו הקו זרם.

מאחר והזרימה אינרציאלית, נוכל להשתמש במשוואת ברנולי על שתי נקודות באותו הקו זרם. נזניח כבידה, ונבחר נקודה בתחילת התעלה ונקודה במרחק מתחילת התעלה:

משימור מסה אינטגרלי זריז (נניח פרופיל זרימה אחיד), נקבל:

נציב בחזרה בברנולי:

כאשר , אנו יודעים ש- . אנו גם יודעים שב- הוא משתנה באופן לינארי, כך ש:

נציב בחזרה בלחץ:

סעיף ג’

נחשב את הכוחות הפועלים על המוצק שמושפע מהקפיץ:

דג”ח על הפלטה העליונה.

מהנתונים, אנו במצב מתמיד, כך שהגענו לשיווי משקל, ולכן שקול הכוחות הוא :

נשים לב שהכוח שהזורם מפעיל על הפלטה הוא פשוט סכימת הלחץ לאורך הקיר:

מחוק הוק:

נציב בחזרה בשקול כוחות:

סעיף ד’

אם הספיקה קטנה משמעותית, אז הזרימה תהפוך להיות צמיגה, בה הזרם הוא מלחץ גבוה ללחץ נמוך. מאחר ובכניסה הלחץ הוא , מתחת לפלטה הלחץ יהיה קטן יותר ממצבו הנוכחי. כיוון שהלחץ מעל הפלטה יהיה גבוה יותר מהלחץ מתחתיו, נסיק שהפלטה תרד.

שאלה 3

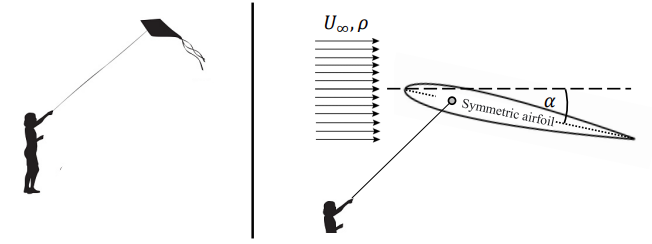
העפיפון המתואר בבעיה.

סעיף א’

מאחר והכנף סימטרית, אין מומנט סביב הרבע מיתר:

סעיף ב’

דג”ח על הכנף.

נדרוש שסכום המומנטים סביב נקודת התפיסה תתאפס:

מהגדרת מקדם העילוי:

עבור כנף סימטרית, אנו יודעים כי:

נציב בחזרה בשקול מומנטים:

ולכן:

סעיף ג’

דג”ח על הכנף. הכוחות לא בהכרח משורטטים איפה שהם פועלים - זה לא רלוונטי לשאלה.

בהנחה ואנו בשיווי משקל, בכיוון מתקיים:

בכיוון :

ולכן:

סעיף ד’

לפי בלסיוס אנו יודעים ש:

ולכן, משני צדי הכנף, כוח הגרר הוא:

ולכן:

סעיף ה’

לא בחומר

שאלה 4

סעיף א’

עבור גבול הצמיגות נדרוש ש- . לגבי גרר סטוקס, נדרש זרימה צמיגה גיאומטריה כדורית (ספירה) קטנה מספיק.

סעיף ב’

צריך לברר אם בכלל בחומר.

סעיף ג’

המיכל הנתון

ממשוואות ההידרוסטטיקה תחת כבידה:

הצפיפות משתנה לפי , ולכן נפרק למקרים:

בגובה אנו יודעים ש- , ולכן:

נציב בחזרה ב-:

ב- מתקיים:

ומרציפות, ערך זה שווה ל- :

ולכן:

בחרתי ב- חיובי כלפי מעלה, ולכן בתשובות יצאו תוצאות הפוכות.