FLD1_008 תאוריית הכנף הדקה

מבוא

תאוריית הכנף הדקה היא תאוריה הממדלת את הזרימה מסביב לכנף בעזרת הנחות זרימה פוטנציאלית. את הכנף אנו נגדיר בצורה הבאה:

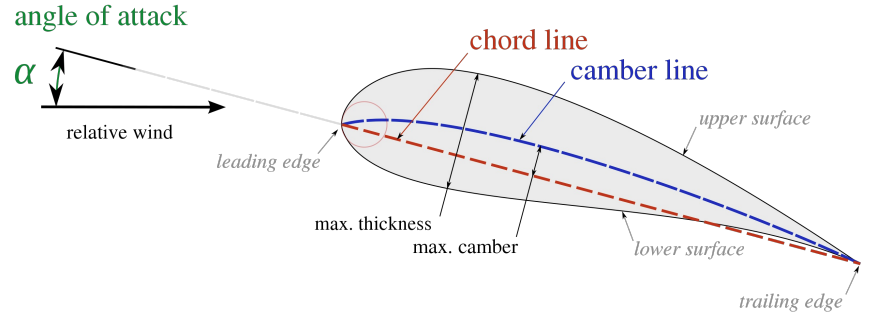
הגדרות החלקים השונים בכנף

• שפת התקפה (Leading edge) - הנקודה הקדמית ביותר של הכנף.
• שפת הזרימה (Trailing edge) - הנקודה האחורית ביותר של הכנף.
• מיתר אווירודינמי (Chord Line) - קו ישר המחבר את שפת התקיפה ושפת הזרימה.
• קו העקימון (Camber Line) - קו שנמצא במרחק שווה מהמשטח העליון ומהמשטח התחתון של פרופיל הכנף.
• עקימון מקסימלי (max camber) - המרחק הגדול ביותר בין המשטח העליון והתחתון.
• עובי מקסימלי (max thickness) - המרחק הגדול ביותר בין המשטח העליון והתחתון.
• זווית תקיפה (angle of attack) - הזווית הנוצרת בין כיוון הזרימה והמיתר.
• מרכז אווירודינמי - נקודה לאורך המיתר עבור שינוי של זווית ההתקפה לא משנה את המומנט הפועל על הכנף.

משפט קוטה-ז’וקובסקי

משפט:

עבור זרימה דו-ממדית פוטנציאלית מסביב לכנף קבועה, הנעה במהירות קבועה (או שנמצאת בזרימה מציפה), כוח העילוי ליחידת עומק נתון ע”י:

כאשר הוא צפיפות הזורם; הוא מהירות הזרימה המציפה; ו- הוא עוצמת הערבול (סירקולציה) מסביב לכנף.
הסימון ל- מדגיש את העובדה ש- הוא כוח העילוי ליחידת עומק, כי אנחנו דנים במקרה דו-ממדי. בכללי, כוח עילוי מסמנים ב-.

פיתוח (עבור גליל, לא עבור כנף כי זה מסובך):
בפרק קודם, ראינו שעבור גליל מסתובב, הלחץ על השפה של הגליל נתון ע”י:

נוכל לסכום את לחץ זה בכיוון :

סכום לחץ זה הוא בעצם הכוח שהזורם מפעיל על הגליל - כוח העילוי.

הרחבה של ביטוי זה לכנף היא מעיקה.

פונקציית הפוטנציאל של כנף

באופן דומה לגליל נרצה למדל את פונקציית הפוטנציאל של כנף בזרימה מציפה. כלומר, אנו צריכים שהיא תקיים את תנאי אי-החדירה מסביב לכנף, וגם את משוואת לפלס - .

ניתן להראות ע”י שליטה מעולה בחדו”א שפונקציית פוטנציאל זו היא סופרפוזיציה של אינסוף ערבולים שמרכזם על קו העקימון:

אין צורך באמת להבין מה קורה כאן. מה שחשוב הוא ש- מייצג את המהירות סביב הכנף, הוא המיקום של מהירות זו, והוא שווה לסכום של אינסוף ערבולים בעוצמה (שכל אחד מהם ממקומם ב-). האינטגרציה מתרחשת בין ל-, כאשר הוא אורך המיתר האווירודינמי.

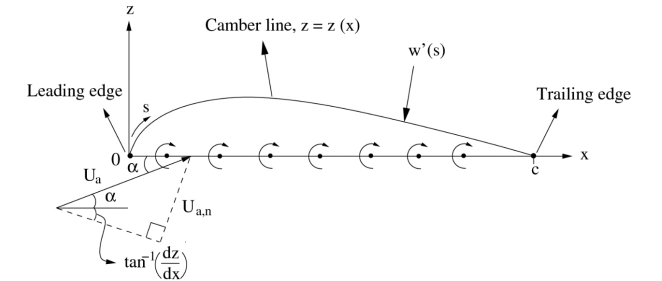
המחשה אם זה עוזר. שימו לב שהעקומה שמופיעה היא לא הכנף עצמה, אלא רק קו העקימון שלה.

הבעיה כאן היא שאין תנאי על . כלומר כרגע, לא משנה מה עוצמת הערבולים - הסירקולציה, ה- שמצאנו מקיים את כל התנאים - אי חדירה ומשוואת לפלס. נצטרך עוד תנאי כדי לקבל פתרון חד משמעי לשדה הזרימה.

תנאי קוטה

תנאי קוטה הוא תנאי הקובע שעבור זרימה קבועה, הזרימה תגיע אל קצה הכנף משני הכיוונים, כשהזרימה שעברה מתחת לכנף לעולם לא תזרום מעל לכנף, וזרימה שעברה מעל לכנף לעולם לא תזרום מתחתיה. כלומר, זהו תנאי פיזיקלי. כל פתרון של שדה הזרימה שלא מקיים את תנאי זה, הוא אולי נכון מתמטית, אבל הוא פשוט לא הגיונית פיזיקלית.

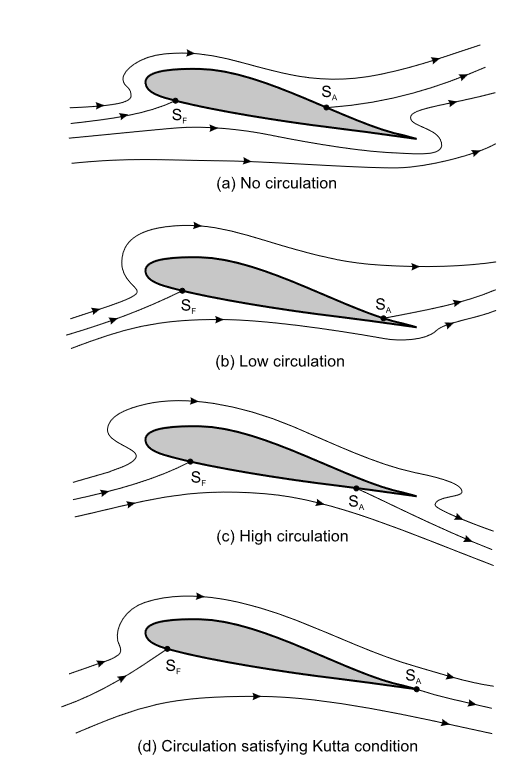
סירקולציות שונות סביב כנף (Houghton et al., 2017).

כדי לקיים את תנאי קוטה, הסירקולציה סביב הכנף צריכה להיות שונה מאפס, וסופית.

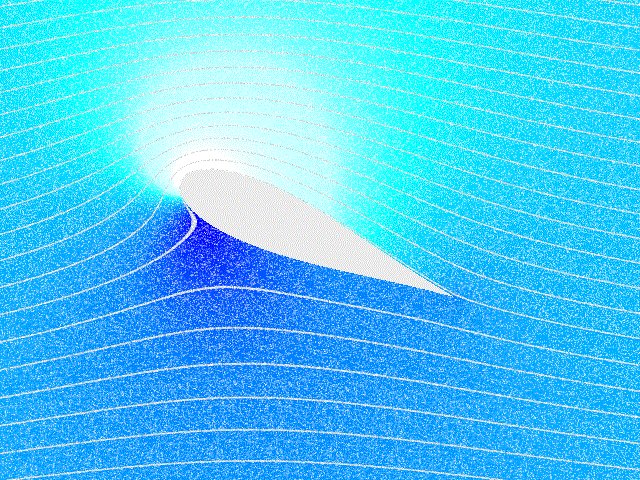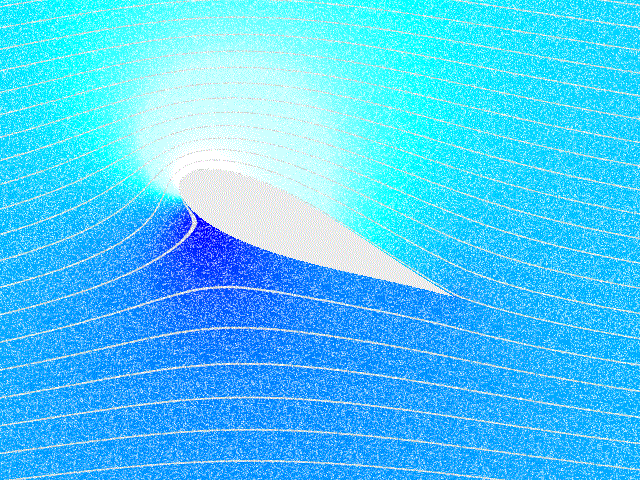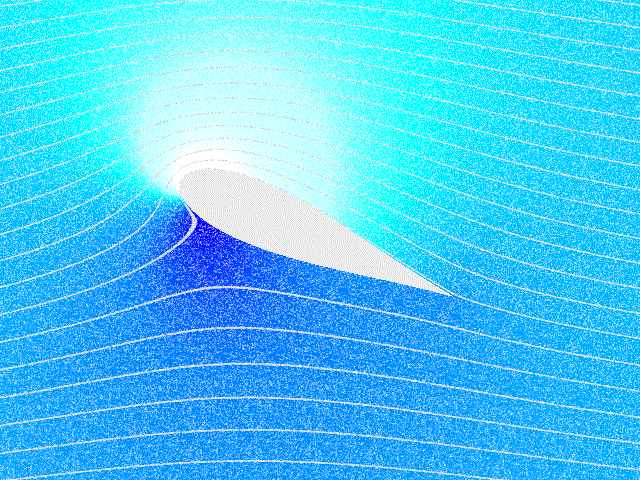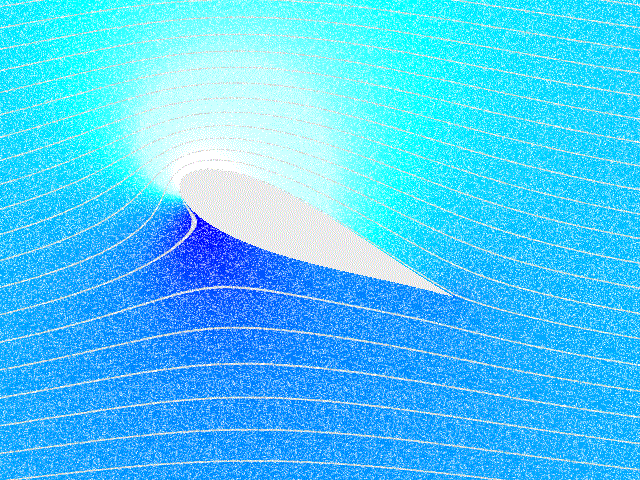
זרימה של זורם בלתי דחיס, אינרציאלי סביב כנף. כהות הצבע הכחול מתארת את הלחץ (הכהה ביותר הוא הלחץ הגבוה ביותר) (“Kutta Condition,” 2024).

כאשר מתחשבים גם בתנאי זה, אנו מקבלים פתרון יחיד ל-:

כאשר:

ו- היא זווית ההתקפה; הוא פונקציית העקימון (camber line).
בנוסף, אנחנו מבצעים התמרה מ- ל- בצורה הנתונה ע”י:

גם כאן לא כל כך קריטי להבין מה קורה, אבל המקדמים כן יהיו שימושיים בהמשך, וכן נצטרך להיעזר בהתמרה מ- ל- אם פונקציית קו העקימון שלנו, , תהיה נתונה בקואורדינטות .

עילוי ומומנט של כנף

מקדם העילוי והמומנט

נהוג להגדיר גודל מנורמל של כוח העילוי, לפי המהירות המציפה, בצורה הבאה:

הגדרה:

מקדם כוח העילוי מוגדר כ:

באותו אופן, נהוג גם להגדיר מקדם מומנט:

הגדרה:

מקדם המומנט סביב נקודה כללית מוגדר כ:

נשים לב ששני גדלים אלו, הם גדלים חסרי יחידות.

נוכל להשתמש בגרסה דיפרנציאלית של משפט קוטה-ז’וקובסקי כדי לקבל ש:

נציב בהגדרת מקדם העילוי ונקבל:

מסימטריות האיברים בתוך האינטגרל, כל הביטוי הזה מצטמצם לפשוט:

נוכל גם למצוא את מקדם המומנט סביב שפת ההתקפה (הנקודה הכי קדמית, שאנו מגדירים כראשית הצירים, ):

הערה (תודה לעידן וולף שעלה על זה):

הסיבה לסימן מינוס היא שמערכת הצירים שלנו היא כלפי מעלה ו- ימינה, כך שמומנט חיובי הוא בעצם לתוך המסך, והמומנט שהעילוי יוצר ביחס ל- הוא החוצה מהמסך.

לאחר הצבת נקבל:

בעזרת שני מקדמים אלו, אנו יכולים למצוא את מקדם המומנט בכל נקודה. אנו יכולים גם למצוא את הנקודה בה פועל מרכז הכוח של כוח העילוי (מרכז המסה של הכוח המפורס). נדרוש שסכום המומנט שנוצר ע”י כוח העילוי במרחק משפת ההתקפה, והמומנט סביב שפת ההתקפה יהיה שווה לאפס:

נציב את הערכים שכבר קיבלנו:

כיוון ש- :

נשים לב שאם הכנף סימטרית, אז קו העקימון הוא פשוט הפונקציה - הוא מתלכד עם המיתר האווירודינמי. במצב זה:

במקרה ספציפי זה, נקבל:

כלומר, ברבע המיתר, מקדם המומנט מתאפס:

המשמעות היא שעבור כנף סימטרית תחת זרימה מציפה, המומנט כתוצאה מכוח העילוי סביב נקודת רבע המיתר - מתאפסת.

במקרה הכללי, בו הכנף לא בהכרח סימטרית, מקדם המומנט סביב רבע המיתר נתון ע”י:

תרגילים

שאלה 1

קו הקימור של פרופיל כנף דקה באורך מיתר נתון ע”י המשוואה הבאה:

סעיף א’

האם הכנף היא כנף סימטרית?

פתרון:
מאחר ופונקציית קו הקימור היא לא פשוט , נסיק כי הכנף לא סימטרית.

סעיף ב’

שרטטו סכמתית את צורת קו הקימור ומצאו את הקימור המקסימלי.

פתרון:

צורת קו הקימור

סעיף ג’

חשבו את מקדם העילוי, .

פתרון:
נרצה להשתמש במשוואת מקדם העילוי:

כאשר את נוכל למצוא ע”י האינטגרלים:

לכן, נחשב את הנגזרות של לפי בכל אחד מהתחומים:

באינטגרלים, אנו בהחלפת משתנים, ע”י ההתמרה:

לכן, נרצה לדעת מהם גבולות התחומים במונחים של :

נציב באינטגרלים:

נחשב על הדרך גם את כי נצטרך אותו בהמשך:

נוכל כעת למצוא את מקדם העילוי:

ולכן:

סעיף ד’

חשבו את זווית התקיפה עבור המקרה בו כוח העילוי שווה לאפס, כפונקציה של .

פתרון:
מהגדרת מקדם העילוי:

נדרוש , ונקבל שגם . מסעיף קודם, כאשר , נקבל:

סעיף ה’

חשבו את מקדם המומנט ברבע מיתר, .

פתרון:
נציב פשוט בנוסחה למקדם המומנט ברבע מיתר:

סעיף ו’

חשבו את המומנט הפועל בשפת ההתקפה עבור זווית של .

פתרון:

הערה:

אפשר פשוט להציב בנוסחה למקדם מומנט סביב שפת ההתקפה, זה פשוט עוד שיטה.

ממשפט קוטה-ז’וקובסקי, אנו יכולים להסיק שהמומנט הפועל ביחס לכל נקודה ע”י כוח העילוי, נתון ע”י:

האינטגרל השמאלי שקיבלנו הוא פשוט המומנט סביב הראשית, (האפס). האינטגרל הימני הוא כוח העילוי, כפול . כלומר קיבלנו:

כאשר הוא כוח העילוי. נוכל לחלק הכל ב- :

מופיעים לנו כאן הגדרת מקדם המומנט סביב , סביב הראשית, ומקדם העילוי:

אנחנו כבר מצאנו את מקדם המומנט ברבע מיתר, כלומר כאשר . נציב: