FLD1_003 חוקי שימור אינטגרליים

תכונות נפח בקרה

עבור נפח בקרה כלשהו, אנו יכולים להגדיר מספר תכונות (בתרמודינמיקה - תכונה אינטנסיבית) שמוגדרות עבור כל נקודה בתוך הנפח בקרה (לפי הנחת הרציפות. למשל, עבור כלל המסה, נוכל להגדיר צפיפות:

עבור סך האנרגיה:

סך תנע (קווי):

סך תנע זוויתי:

נשים לב שכל תכונה אנו מגדירים בצורה כללית מאוד דומה:

כאשר אותיות גדולות הן סך גודל התכונה בנפח בקרה, ו- מייצג את גודל התכונה המקומית (התכונה הסגולית).

משפט ריינולדס לנפח בקרה

משפט:

משפט ריינולדס לנפח בקרה קובע ש:

באופן מפורש:

כאשר הוא מהירות החלקיקים ביחס לנפח בקרה ו- הוא וקטור הכיוון של הנורמל לגבול (משטח) - החוצה מנפח הבקרה.

שימו לב:

שוב, מצביע החוצה מנפח הבקרה - זהו וקטור שתלוי אך ורק בגאומטריית נפח הבקרה, ובכלל לא בשדה הזרימה!

כעת נוכל להשתמש בחוקים ידועים ולהפעיל אותם על המשוואה, כדי לקבל את חוקי השימור האינטגרליים.

חוק שימור המסה האינטגרלי

עבור מסה, נציב במשוואת ריינולדס:

מחוק שימור המסה, אנו יודעים שאין שינוי במסה, כך ש- . נקבל את חוק שימור המסה האינטגרלי:

חוק שימור התנע האינטגרלי

אם נציב למשוואת ריינולדס, נקבל:

מחוק שני של ניוטון, . חוק זה תקף לכל החלקיקים. נציב, ונקבל את חוק שימור התנע האינטגרלי:

כאשר הוא סך הכוחות הפועלים על הזורם.

הערות:

1. המהירות נמדדת ביחס למערכת הצירים ואילו נמדדת ביחס לנפח בקרה. לפעמים המערכת צירים תהיה צמודה לנפח בקרה, ואז באמת .
2. לפעמים נבחר במערכת צירים שהיא לא אינרציאלית - כלומר מערכת צירים מאיצה. במקרה זה, אנו צריכים להציע תיקון לחוק שני:

כאשר הוא תאוצת מערכת הצירים, ו- הוא סך הכוחות הפועלים על הזורם.

לפעמים נרצה לפרק את לכוחות המעטפת (מאמצים הפועלים על מעטפת הזורם) וכוחות הגוף (כוח ליחידת נפח הפועל על כלל נפח הזורם) (בדומה למבוא לאלסטיות):

הערה:

אמנם מייצג כוחות גוף, אבל הוקטור הוא וקטור תאוצה. הוא למעשה התאוצה כתוצאה מכוחות גוף כמו למשל כבידה.

משוואת ברנולי

• נרחיב עוד על הנושא באינרציה.

עבור נוזלים בלתי דחיסים, ניתן להניח שצפיפותם אחידה. מאחר וברנולי ביצע את ניסוייו על נוזלים בלתי דחיסים, וצמיגות זניחה, הנוסחה שהוא פיתח עבורם תקפה רק להם.

נוסחה:

משוואת ברנולי קובעת כי:

כאשר הוא מהירות הנוזל בנקודה; היא תאוצת הנוזל כתוצאה מכבידה; הוא גובה הנוזל יחסית לנקודה ייחוס קבועה, וכאשר חיובי כלפי מעלה; הוא הלחץ בנקודה, ו- הוא צפיפות הנוזל (שהיא אחידה).

כאשר הזורם:

• תמידי
• צמיגותו זניחה
• בלתי דחיס

ושתי נקודות על אותו הקו זרם, נוכל להשתמש עבור שתי הנקודות במשוואת ברנולי:

תרגילים

טיפים למבחן מדניאל שרושם את השאלות נפח בקרה למבחן:

• יש להגדיר את נפח הבקרה בצורה טובה.
• יש להגדיר את מערכת הצירים באופן מדויק - כולל מיקום.
• נפח בקרה תמיד צמוד לזורם - לא למוצק שעוטף אותו בהכרח!
• מסה לא נוצרת ולא נהרסת.

שאלה 1

נוזל בעל צפיפות זורם בתעלה דו-ממדית בעלת גובה . פרופיל המהירות בכניסה לתעלה הינו לינארי , וביציאה פרופיל המהירות הוא פרבולי:

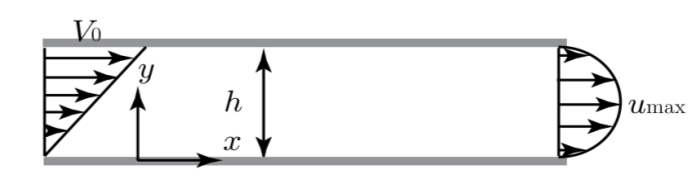
סעיף א’

מצאו את המהירות הממוצעת בחתך היציאה בתלות ב-.
פתרון:
נבחר כנפח בקרה את את הצינור. המהירות הממוצעת נתונה ע”י:

נציב את המהירות היציאה:

סעיף ב’

בטאו את כתלות ב-.
פתרון:

סכימה של הנפח בקרה.

לפי חוק שימור המסה האינטגרלי:

נפח הבקרה שלנו ו- קבוע כך שהאיבר הראשון מתאפס. נשים לב כי גם נוכל לחלק ב-:

שאלה 2

נוזל בעל צפיפות זורם בצינור נקבובי בעל רדיוס . הנוזל נכנס לצינור במהירות אחידה וזורם החוצה מהדפנות של הצינור בצורה רדיאלית ואקסי-סימטרית עם פילוג המהירות הבא:

מצאו את הספיקה המסית שעוברת בצינור בחתך .

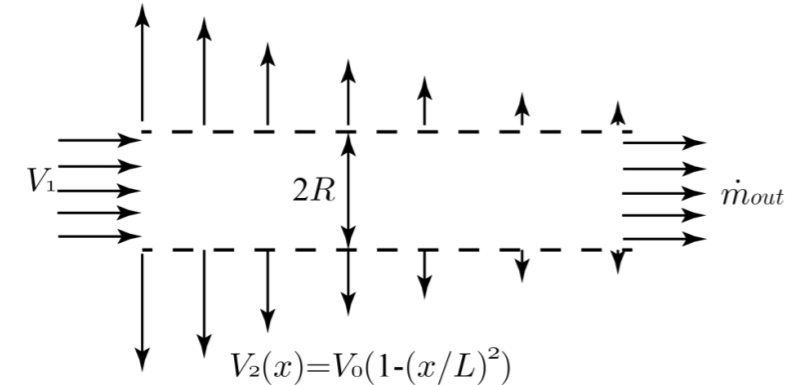
פתרון:
לפי שימור מסה:

הנפח קבוע והצפיפות קבועה כך שהאיבר הראשון מתאפס. נחשב את האינטגרלים האחרים בנפרד:

נציב בחזרה בשימור מסה:

שאלה 3

נתונה כוס פלסטיק בעלת צורה של חרוט קטום בעל גובה , ובסיסים ו-, בהתאמה. הכוס מלאה במים עם צפיפות . מחררים את תחתית הכוס, כך שמים מתנקזים דרך חריר קטן מאוד עם רדיוס . ידוע כי מהירות ביציאה מהחריר תלויה בגובה רגעי של המים לפי .

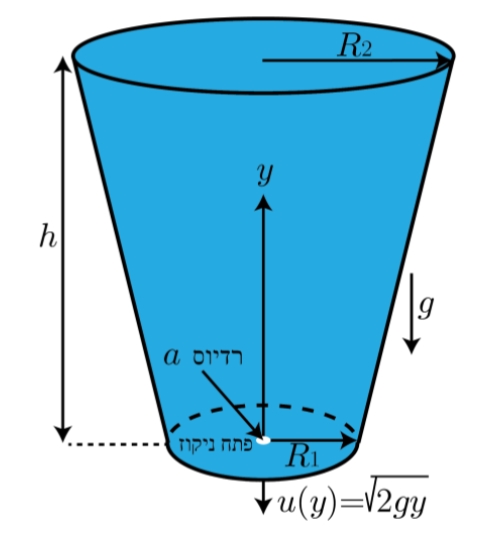
סכמת הבעיה.

סעיף א’

בהנחה שהגובה התחלתי של המים הינו , מצאו את זמן הריקון כתלות בנתוני השאלה.
פתרון:
נבחר נפח בקרה צמוד כוס, היורד עם מפלס המים. לפי שימור מסה:

נחלק ב- כי הוא קבוע:

נפתור כל אינטגרל בנפרד:

נציב בחזרה בשימור מסה:

נשים לב כי יש קשר לינארי בין ל-:

ולכן:

נסמן .
כעת נוכל לרשום ביטוי לנפח כתלות ב- (האינטגרל הראשון, ללא הגזירה לפי הזמן).

נוכל כעת למצוא את הנגזרת לפי הזמן:

נציב בשימור מסה:

זוהי משוואה פרידה, שכאשר נציב את התנאי התחלה , נקבל לאחר פתרון:

לאחר קירובים והזנחות, נוכל לרשום:

כאשר:

סעיף ב’

העריכו את זמן הריקון עבור:

נקבל:

שאלה 4

בתעלה דו-ממדית בעלת גובה מתקיימת זרימה תמידית ובלתי דחיסה (צפיפות ) סביב גוף סימטרי הממוקם מרכז התעלה, כמתואר בציור:

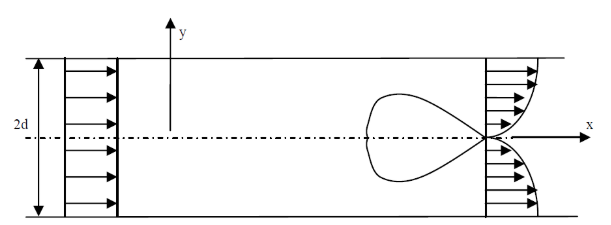
סכימת התעלה.

רחוק לפני הגוף מהירות הזורם אחידה והלחץ אחיד. מיד אחרי הגוף ניתן להניח כי הלחץ אחיד בחתך וכי קיים פרופיל מהירות פרבולי (כפול) בו המהירות מתאפסת על ציר הסימטריה וגם כי

סעיף א’

מצאו את פרופיל המהירות מיד אחרי הגוף במונחי .
פתרון:
נגדיר את נפח הבקרה על המחצית העליונה של הזורם (, לא כולל הגוף הסימטרי). לפי חוק שימור המסה האינטגרלי:

נפח הבקרה לא משתנה עם הזמן, ו- אחיד וקבוע, כך שהביטוי הראשון מתאפס. נוכל להמשיך לפתח את הנוסחה, כאשר נוכל לחלק ב-:

כאשר בחרנו את פרופיל המהירות בצורה הפרבולית:

אנו יודעים שכאשר , המהירות היא , ולכן :

אנו גם יודעים כי

ולכן:

נציב בחזרה בשימור מסה:

ולכן פרופיל המהירות:

סעיף ב’

בהנחה כי ניתן להשתמש במשוואת ברנולי לאורך קו הזרם , מצאו את כוח הגרר הפועל על הגוף.
פתרון:
לפי חוק שימור התנע האינטגרלי:

הנפח קבוע, הצפיפות קבועה ואחידה, והמהירות קבועה, כך שנוכל לאפס את האיבר הראשון:

כפי שנהוג, נוכל לפרק את לכוחות גוף וכוחות שפה:

במקרה שלנו אין כוחות גוף, וגם את כוחות השפה נוכל לפרק לכל אחד מהגבולות השונים של הנפח הבקרה:

הכוחות שפה (הגזירה) לאורך קו הסימטריה הוא אפסי - משיקולי סימטריה.
הכוחות שפה על הקיר העליון הם גם אפס, כי נתון שבקיר:

האינטגרל על הכנף הוא הכוח שמפעילה התעלה על הזורם. לכן כוח הגרר, הכוח שמפעיל הזורם על התעלה, הוא הנגדי לו:

נציב בחזרה בשימור מסה:

כדי למצוא את ו-, נשתמש במשוואת ברנולי:

נציב בחזרה בשימור מסה:

שאלה 5

נתונה מזחלת צעצוע המבוססת על מיכל מים המתרוקן דרך צינור קטן.

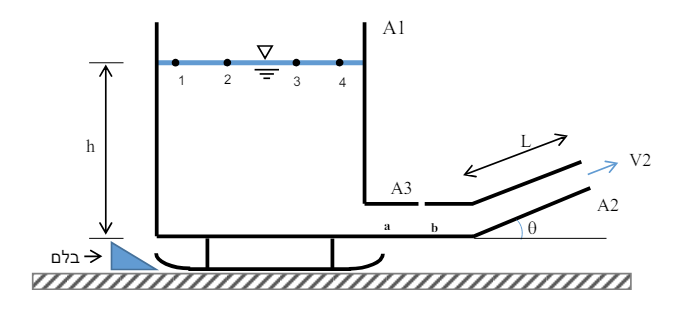
סכימת המזחלת.

כפי שמוצג בציור, מיכל המים במיכל המים המותקן על המזחלת הינו בעל שטח חתך וגובה המים בו הינו . המים במיכל מתרוקנים לסביבה הנמצאת בלחץ אטמוספרי דרך צינור בעל שטח חתך . קצה הצינור, באורך מוטה בזווית ביחס לאופק וניתן להניח כי . כמו כן, ניתן להניח כי פתח הצינור קטן לעומת שטח המיכל, , כך שהשינוי בנפח המים במיכל בטווח הזמן המעניין אותנו הינו זניח, מסת המים היא ומסת המזחלת היא , כך ש- .

סעיף א’

מצאו ביטוי למהירות יציאת המים, , דרך הפתח .
פתרון:
נבחר נפח בקרה צמוד זורם. נשים לב כי אנחנו לא יכולים להשתמש בשימור מסה, כי הנחנו שנפח המים במיכל לא משתנה, כך שהמהירות בכניסה (ב-) אפסית, ואז נקבל גם שהמהירות ביציאה היא אפסית.

נוכל להשתמש בברנולי, על כל קו זרם מ- ל-:

סעיף ב’

לאחר זמן קצר, נפער חור קטן, בעל שטח חתך , בחלקו הישר של הצינור, כמתואר בציור. ניתן להניח כי .
ציירו באופן איכותי, כיצד יראה אוסף של קווי זרם שראשיתם בנקודות המסומנות 1-4 על פני המים.
פתרון:

קווי זרם שראשיתם בנקודות 1-4.

סעיף ג’

מצאו ביטוי למהירות לאחר היווצרות החור.
פתרון:
המהירות לא השתנתה כתוצאה מהיווצרות החור. אולי הספיקה השתנתה, אבל מבחינת משוואת ברנולי, אנו נציב את אותם הנתונים.

סעיף ד’

מצאו ביטוי לגובה סילון המים שנוצר ביציאה מהחריר .
פתרון:
לפי ברנולי:

בשיא הגובה, . גם בפני השטח, . לכן הגובה המקסימלי:

סעיף ה’

מצאו ביטוי להפרש הלחצים בין הנקודות ו- הנמצאות בחלקו הישר של הצינור (לפני ואחרי החריר). ניתן להניח כי התנאים בשטח החתך של הצינור אחידים.
פתרון:
שוב, ברנולי בין ל-:

מתקיים , ולכן:

ברנולי בין ו-:

מתקיים :

אנו יודעים ש- .
כדי למצוא את , נבצע שימור מסה. נבחר את נפח הבקרה הבא:

נפח בקרה עם כניסה אחת ושתי יציאות.

לפי שימור מסה:

נוכל להציב את בחזרה בהפרש לחצים כדי לקבל את הביטוי הדרוש. אבל לא נעשה את זה כי דניאל לא הספיק.

סעיף ו’

לאחר זמן קצר נוסף, משחררים את הבלם והמזחלת מתחילת לנוע.
בהנחה שעל המזחלת פועל גם כוח החיכוך הקינטי מהצורה , כאשר הוא מקדם חיכוך ידוע ו- הוא הכוח הנורמלי המופעל על המשטח, מצאו את הזווית עבורה המזחלת תנוע במהירות קבועה. לצורך פישוט החישוב, ניתן להניח ש- קטנה מאוד.

פתרון:
כדי שהעגלה תנוע במהירות קבועה, נצטרך שכלל הכוחות עליה יתאפסו.

דג”ח על המזחלת

משקול כוחות:

משתי המשוואות נקבל כי:

נרצה כעת למצוא את . נבחר את הנוזל במזחלת כנפח הבקרה, עד היציאה שלו ב- ו-. מחוק שימור התנע האינטגרלי:

נפח הבקרה קבוע עם הזמן (נוכל להזניח את הכמות הזעירה של המים שיוצאת מהמיכל) וצפיפותו גם כן אחידה וקבועה, כך שנוכל לאפס את האינטגרל על הנפח:

התנועה היחידה היא רק מהיציאה ו- ולכן האינטגרל בצד ימין הופך ל:

כאשר נציב בחזרה בשימור תנע, נקבל עבור כל כיוון ש:

כוח זה הוא הכוח שהמזחלת מפעילה על הנוזל, ולכן הנגדי לו הוא הכוח שהנוזל מפעיל על המזחלת:

נציב בביטוי שמצאנו ל-:

תחת הנחת זוויות קטנות: