שאלה 1
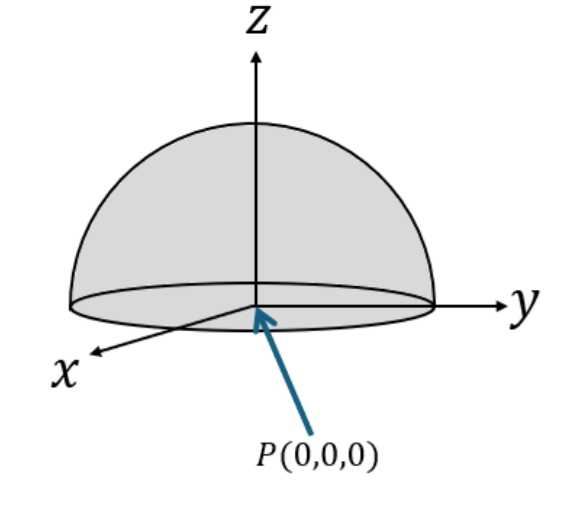
סכמת הבעיה.
העבודה שיש להשקיע כדי להביא מטען
נוכל להניח שהפוטנציאל באינסוף אפסי, כך ש:
מפוטנציאל של גוף רציף אנו יודעים ש:
נציב בחזרה ב-
שאלה 2
לפי חוק גאוס:
כדי לחשב את המטען הפנימי, נשים לב שהתיבה עוטפת חצי מכל הכדור, ולכן נוכל לצמצם את גבולות האינטגרציה לגבולות הכדור (ואז נחלק ב-
כאשר נזכיר כי:
נציב בחזרה בשטף:
שאלה 3
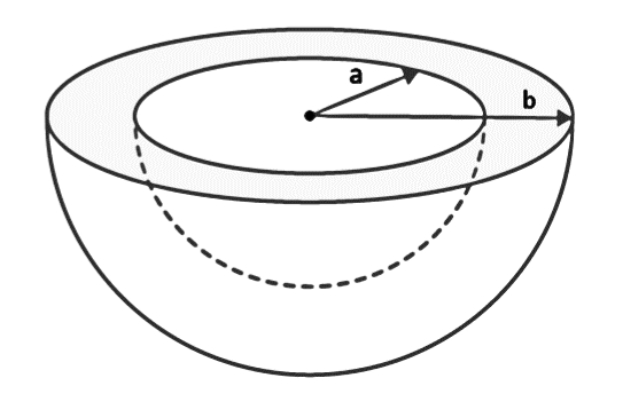
סכימת הקליפה.
נחשב לפי הגדרה:
באופן דיפרנציאלי:
נשים לב משיקולי סימטריה כיוון השדה שלנו הוא רק ב-
מגיאומטריה:
לפי חוק קולון:
מאחר ו-
נוכל כעת לסכום לכל אורך הנפח:
נסכם:
שאלה 4

סכמת הבעיה
לפי חוק אוהם הדיפרנציאלי:
לפי צפיפות זרם חשמלי:
מסימטריה אנו יודעים כי
נציב בחזרה בחוק אוהם:
נציב בחוק גאוס הדיפרנציאלי:
נשים לב ש-
ולכן:
שאלה 5
לאחר זמן רב, אנו מגיעים לשיווי משקל, כך שהמתח על כל הקבלים זהה. לכן, מאחר והקיבול עליהם זהה, ונשמר המטען, נסיק כי:
שאלה 6
לפי חוק אמפר, נבנה לולאת אמפר ברדיוס
נשים לב כי
נציב את התנאי
שאלה 7
נפרק את החרוט לטבעות נושאות זרם
כדי למצוא את
נציב בחזרה ב-
נציב בשדה מגנטי של טבעת:
נשים לב כי:
נשים לב ש-
נוכל כעת לבצע אינטגרציה:
שאלה 8
לפי חוק אוהם:
במקרה שלנו, נוצר כא”מ כתוצאה מהשינוי בשטף המגנטי, לפי חוק פאראדיי:
השטף המגנטי תלוי בזווית של המשולש (
כאשר השטח של המשולש הוא:
ולכן:
ולכן הכא”מ:
ולכן הזרם:
כך שהזרם המקסימלי הוא:
שאלה 9
לפי טעינה של מעגל RL:
במקרה שלנו:
נציב באנרגיה אגורה במשרן:
שאלה 10
נשים לב שהצפיפות של המיתר היא
אנו יודעים שהגבולות על התדרים (כתדרי יסוד) נעים בין
ולכן טווח המתיחויות הוא:
שאלה 11
לפי גל אלקטרומגנטי, נוכל לרשום את הגל בצורה הבאה:
ולכן:
מאחר ו-
בנוסף, אורך הגל הוא
שאלה 12
לפי ניסוי יאנג, אנו יודעים שנקבל התאבכות בונה ב:
דרוש המיקום של ההתאבכות מסדר
נשים לב גם שהגובה של הנקודה העליונה נתון גיאומטרית ע”י
גיאומטריית הנקודה הדרושה.
בזוויות קטנות,
נציב נתונים:
ולכן המרחק הדרוש: