ICT1_006 שיטת מקום גיאומטרי של שורשים

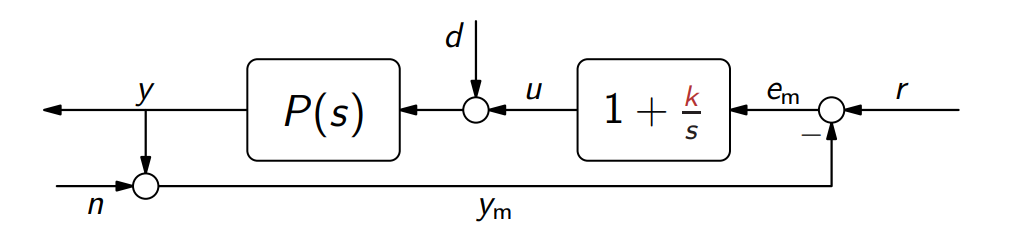
מבוא

נשים לב לשתי דוגמאות של בקר הגבר בחוג סגור.

דוגמה:

עם , והתהליך:

הפולינום האופייני הוא:

לכן, המערכת משוב יציבה פנימית אמ”ם . לפיכך, ייצבנו בעזרת הבקר הגבר מעבר לא יציבה.

מנגד:

דוגמה:

עם , והתהליך:

הפולינום האופייני הוא:

לכן, המערכת משוב יציבה פנימית אמ”ם , שזה טווח מאוד מאוד קטן. כלומר, המערכת משוב גם יכולה להפוך מערכות יציבות, ללא יציבות.

שיטת מקום גיאומטרי של שורשים

נציג כעת שיטה אחרת לבקרה בחוג סגור הנקראת שיטת מקום גיאומטרי של שורשים (מג”ש).

נביט למשל במערכת הבא:

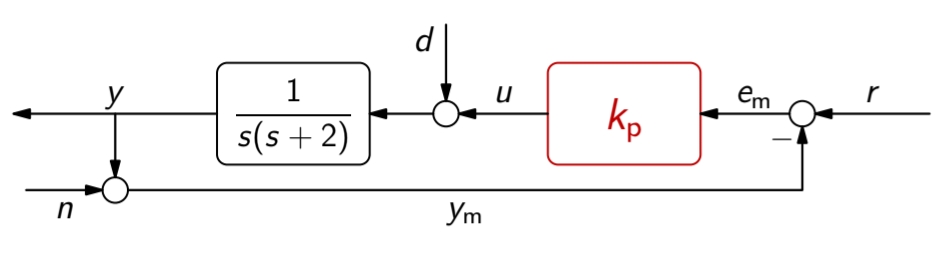
הפולינום האופייני של המערכת הוא , ויש לו שורשים ב:

נציג מספר דוגמאות למיקום השורשים עבור שונים:

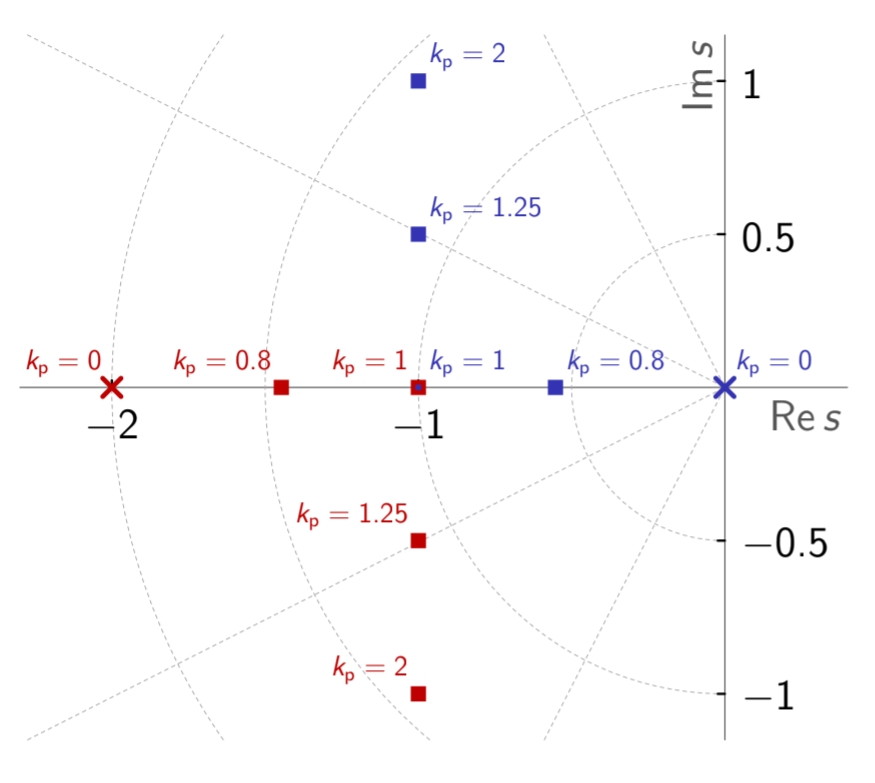
שורשי הפולינום האופייני של המערכת הנתונה עבור ערכי שונים. (Leonid Mirkin’s Homepage, n.d.).

נשים לב שמיקום השורשים של הפולינום האופייני מוגדרים רק עבור צורה מסוימת על המישור המרוכב. אם נשרטט את המיקומים של השורשים של כפונקציה של כל ה--ים, נקבל:

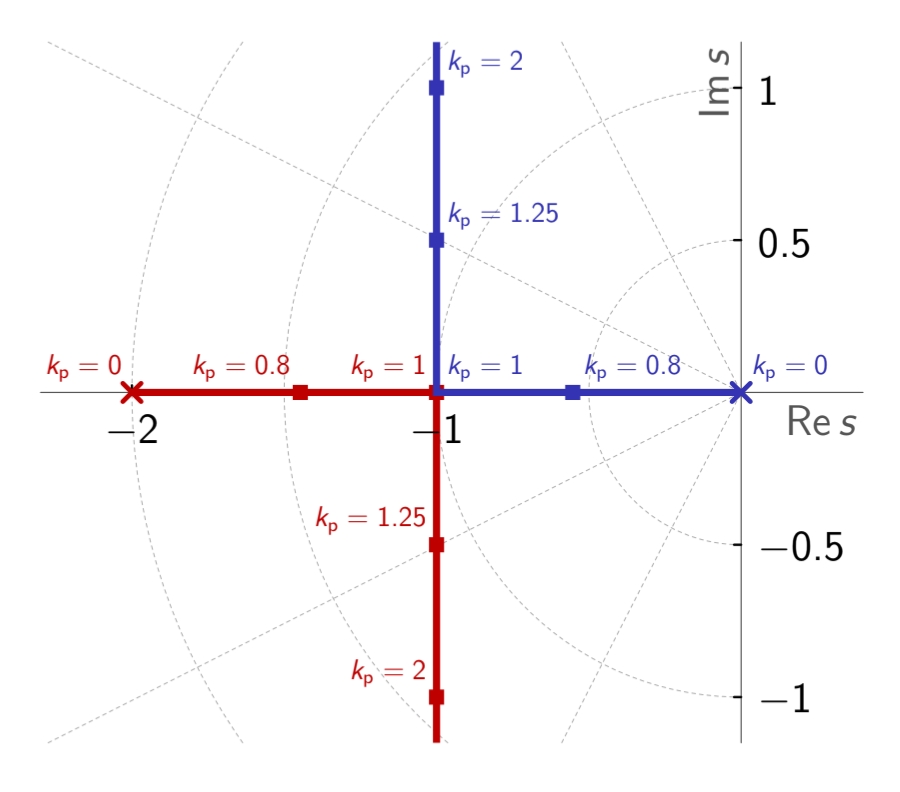
דיאגרמת מג”ש של המערכת הנתונה. (Leonid Mirkin’s Homepage, n.d.).

לדיאגרמה/גרף שקיבלנו קוראים גרף מג”ש (root-locus plot). נשים לב ש:

• עבור קטנים (, מערכת מרוסנת-יתר מסדר שני): ככל ש- גדל, המערכת בחוג סגור נהיית יותר מהירה.
• עבור גדולים (, מערכת תת-מרוסנת מסדר שני): ככל ש- גדל, המערכת נהיית יותר מהירה ( גדל) והמערכת נעשית פחות מרוסנת ( קטן).

אנו רואים שבעזרת המג”ש, אנו משיגים תיאור גיאומטרי ל:

• ניתוח יציבות - מערכות בחוג סגור יציבות אמ”ם כל השורשים שלהם ב-LHP הפתוח.
• ניתוח אופן תגובת מעבר - כפי שראינו בניתוח מודלי, היחס ע”ע של המערכת קשור לריסון והתדירות הטבעית של המערכת.

ייצוג מג”ש של הפולינום האופייני

נביט במערכת הבאה:

הפולינום האופייני של מערכת זו הוא מהצורה:

או, באופן שקול, כ:

ייצוג זה נקרא הייצוג מג”ש של הפולינום האופייני ונניח מעתה ש- הוא proper.

הערה:

במקרה ו- לא proper, נוכל להחליף את עם כדי שנקבל שהוא proper.

נוכל גם לקבל את הייצוג מג”ש מפרמטרים אחרים. למשל, עבור המערכת הבאה:

עבורו:

מה שמוביל לייצוג

תהליך מג”ש

בהינתן

כאשר:

נפתח מספר כלים לשרטוט ענפי המג”ש כאשר משתנה מ- ל-. נקרא לסט כלים אלו תהליך המגש.

הערות:

1. ישנם בדיוק שורשי מיקום, כל אחד מהם מייצג שורש של החוג הסגור.
2. מיקום השורשים סימטרי יחסית לציר הממשי.
3. אם ה--ים שליליים, נחליף עם .

חוק ההגבר והפאזה

נרשום את המג”ש כ:

לכן, לכל ששייך למג”ש, חייב להתקיים:

לשני חוקים אלו קוראים חוק ההגבר וחוק הפאזה בהתאם.
כעת, כדי לבדוק האם נקודה כללית שייכת למג”ש של , אנו רק צריכים לבדוק האם . אם לא, היא לא חלק מהמג”ש. אם כן, אז זה עבור:

הערה:

הפאזה יכולה גם להיות וכו’.

כדי בכלל לדעת האם , נפנה לשתי שיטות:

חישוב אנליטי להגבר ופאזה של :
נביט ב

עבור כללי. לכן, לכל , לפי זהויות טריגונומטריות, מתקיים:

וגם:

הערה:

מאחר ו- , אזי:

חישוב גיאומטרי להגבר ופאזה של :
בהינתן ו- למשל, נשרטט את הנקודה שאנו רוצים לבחון על המישור המרוכב, ונמדוד את הזוויות שלה:

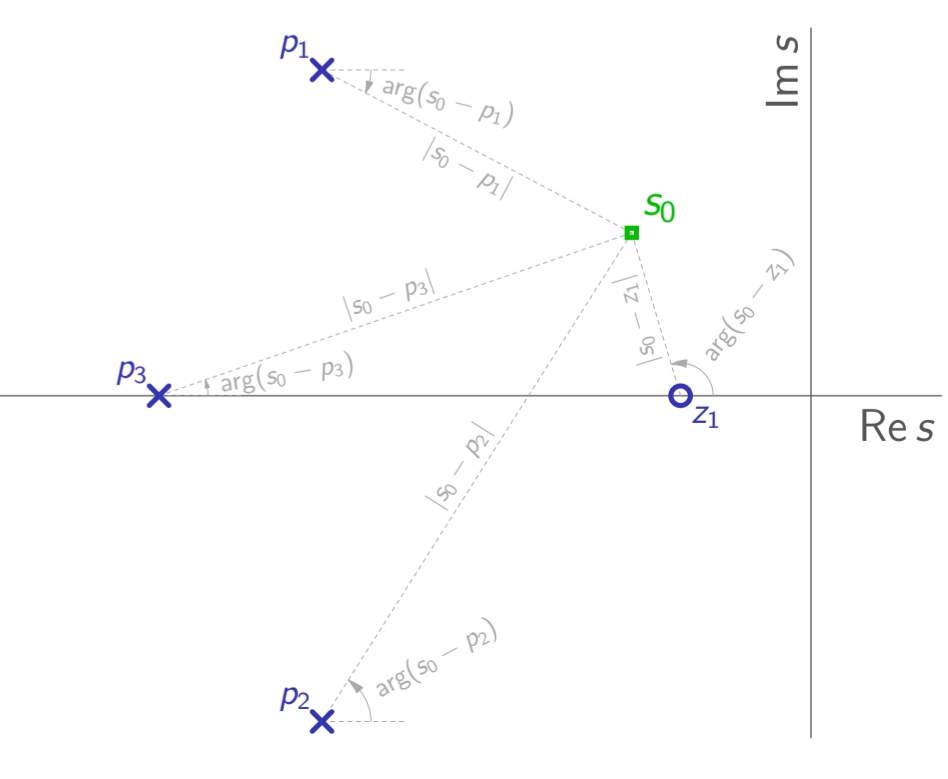
הצגה גיאומטרית של אופן מציאת הפאזה של . (Leonid Mirkin’s Homepage, n.d.).

את הזוויות אנו מודדים ביחס לאפסים והקטבים, נגד כיוון השעון.

נקודות התחלה וסוף

נביט ב:

לכן, עבור (או ), נקבל את המשוואה

עם שורשים המסומנים ב- על המישור המרוכב, ונקודות אלו מייצגות את ההתחלה של ענפי המג”ש (הקווים של אוסף כל השורשים של הפולינום האופייני מ- עד ).

באותו אופן, עבור , נקבל את המשוואה

עם שורשים המסומנים ב- על המישור המרוכב, ונקודות אלו מייצגות את הסוף של הענף.

אבל אם יש התחלות, ו- סופים לענפים, מה קורה עם כל שאר ה- ענפים? האמת היא שניתן להוכיח ענפים אלו פשוט שואפים לאינסוף. אבל, איך הם שואפים לאינסוף? באלכסון? במקביל לציר המדומה? הממשי? להלן התשובה:

אסימפטוטות

ניתן להראות שה- ענפים שואפים לאינסוף לאורך אסימפטוטות שמרכזן במרכזי המסה

עם זוויות:

להלן טבלה שחושבה מראש לערכי :

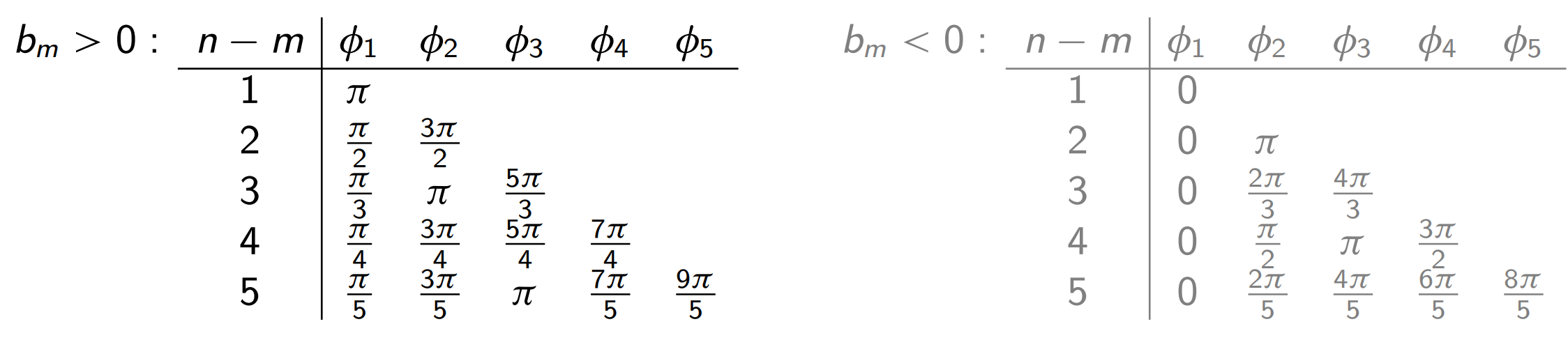
בדוגמה הקודמת למשל, מרכז המסה הוא:

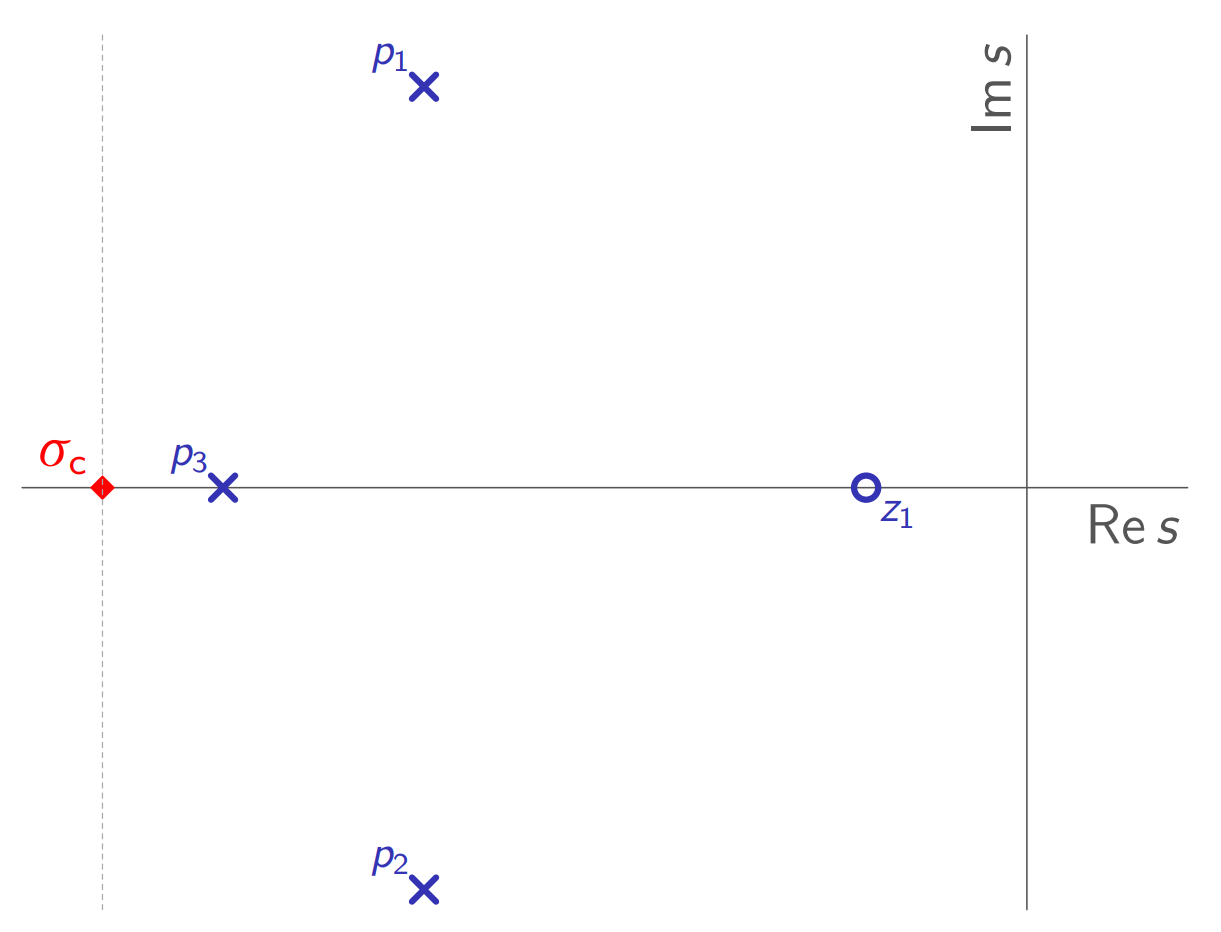
מרכז המסה של הקטבים והאפסים. (Leonid Mirkin’s Homepage, n.d.).

במקרה זה, , כך ש- ו- . את האסימפטוטות שיוצאות ממרכז המסה ניתן לראות בתוצאה הסופית.

מג”ש על הציר הממשי

אם הוא על המג”ש, אז הוא חייב לקיים את חוק הזווית. במקרה המיוחד של הציר הממשי, נשים לב למספר תופעות:

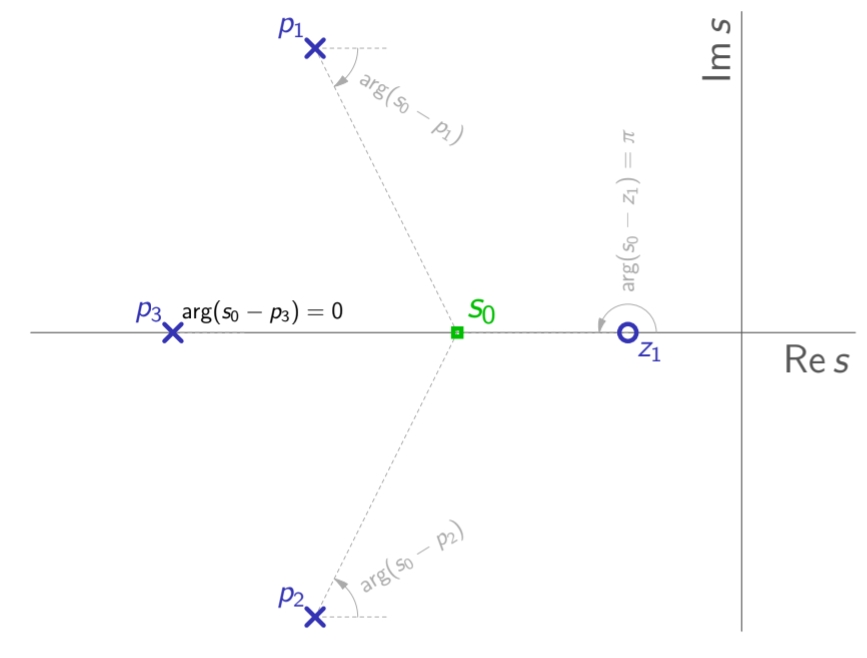
מג”ש של מערכת עם שלושה קטבים ואפס יחיד, לבחינת חוק הזווית עבור על הציר הממשי. (Leonid Mirkin’s Homepage, n.d.).

נשים לב ש:

• סכום הפאזות () מכל זוג מרוכבים מצומדים הוא אפס.
• הפאזה של כל שורש מימין ל- הוא .
• הפאזה של כל שורש משמאל ל- הוא .

נוכל לומר ש:

• אם , אז מתקיים ש:

  כאשר הוא מספר הקטבים והאפסים מימין ל-. לכן, המג”ש קיים על כל החלקים של הציר הממשי משמאל למספר אי זוגי של קטבים ואפסים.

• אם , אז מתקיים ש:

  כאשר הוא מספר הקטבים והאפסים מימין ל-. לכן, המג”ש קיים על כל החלקים של הציר הממשי משמאל למספר זוגי של קטבים ואפסים.

במקרה המתואר לעיל, בהנחה ו- , ישנו רק חלק אחד מהציר הממשי על המג”ש:

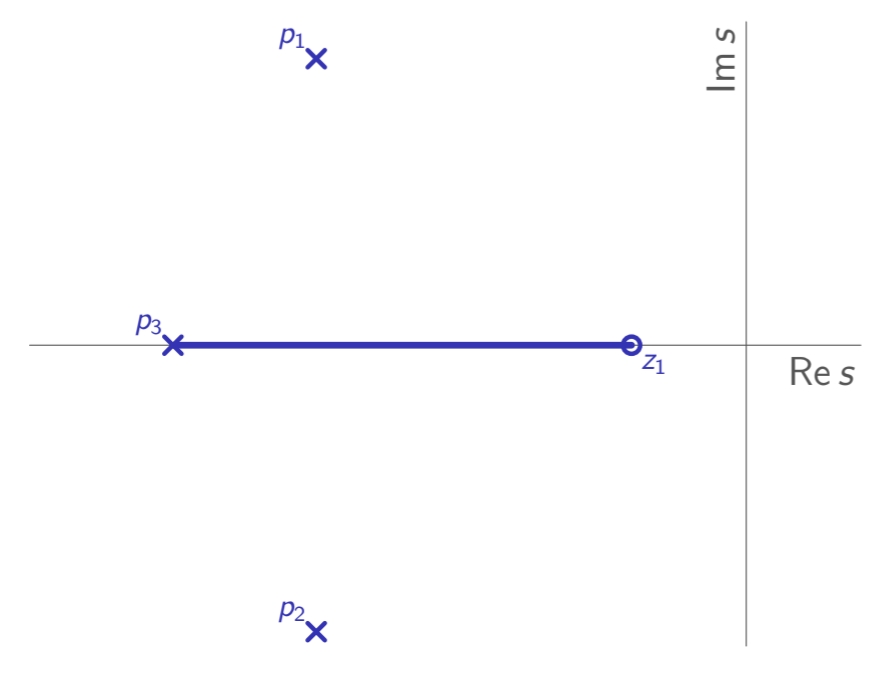
החלק הממשי על המג”ש. (Leonid Mirkin’s Homepage, n.d.).

נקודות הסתעפות על הציר הממשי

יכולות להיות נקודות הסתעפות על הציר הממשי אם ישנם נקודות בהן ל- יש מספר שורשים (כלומר, לפחות 2 שורשים מתלכדים). ניתן להראות ש- היא נקודת הסתעפות עבור כלשהו אם:

חיתוך עם הציר המדומה

נקודות בהן הענפים חוצים את הציר המדומה מאוד חשובות לנו כי הן מעידות על גבולות בהן המערכת יציבה. נקודות אלו מקיימות:

כך שהן תלויות אך ורק בפאזה של תגובת התדירות של .
ישנם שתי שיטות למציאת נקודות אלו:

1. ע”י חוק הפאזה .
2. ע”י טבלת רות.

נשים לב שאנו יכולים גרפית למצוא את התנאי אם נביט בשרטוטי תגובת התדירות של :

1. כאשר הגרף הפולארי של חוצה את הציר הממשי השלילי.
2. כאשר הגרף בודה-פאזה של חוצה את ה-.

זוויות יציאה וכניסה

יהי , כאשר , קטבים פשוטים (כלומר, עם ר”א ור”ג שווים ל-). הענף המתאים יוצא מקוטב זה בזווית:

יהי , כאשר , אפסים פשוטים (כלומר, עם ר”א ור”ג שווים ל-). הענף המתאים נכנס לאפס זה בזווית:

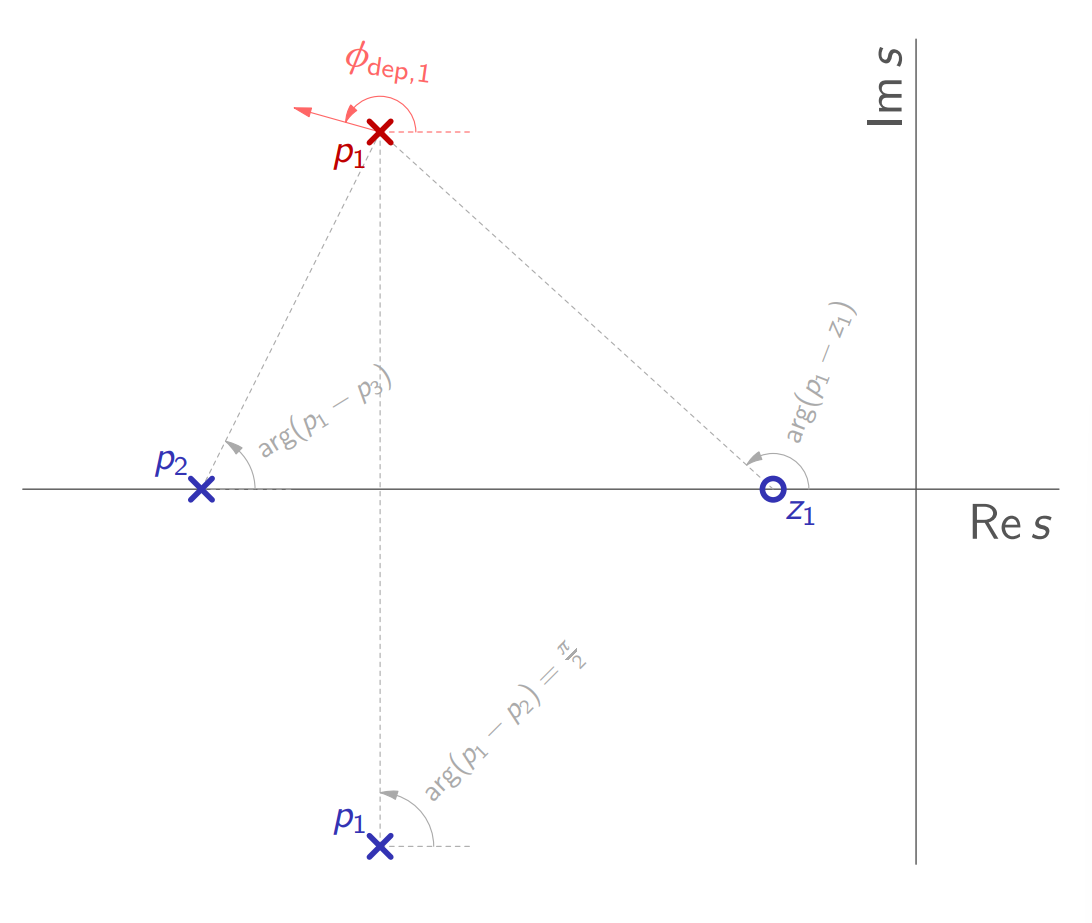
המחשת זווית היציאה מקוטב . (Leonid Mirkin’s Homepage, n.d.).

אלגוריתם: שרטוט המג”ש

לפי החוקים לעיל, נשרטט את המג”ש המלא באופן הבא:

1. נרשום את הפונקציית תמסורת , מהייצוג מג”ש של הפולינום האופייני:
2. נמקם קטבים ואפסים של על דיאגרמת קטבים-אפסים.
3. נשרטט את הענפים על הציר הממשי (משמאל למספר אי-זוגי של קטבים ממשיים ואפסים של ).
4. נשרטט ענפים המסתיימים באפסים. השאר ילכו לאינסוף דרך אסימפטוטות.
5. נמצא את מרכז המסה ואת הזוויות של האסימפטוטות ונשרטט את הענפים שהולכים לאינסוף לאורך האסימפטוטות.

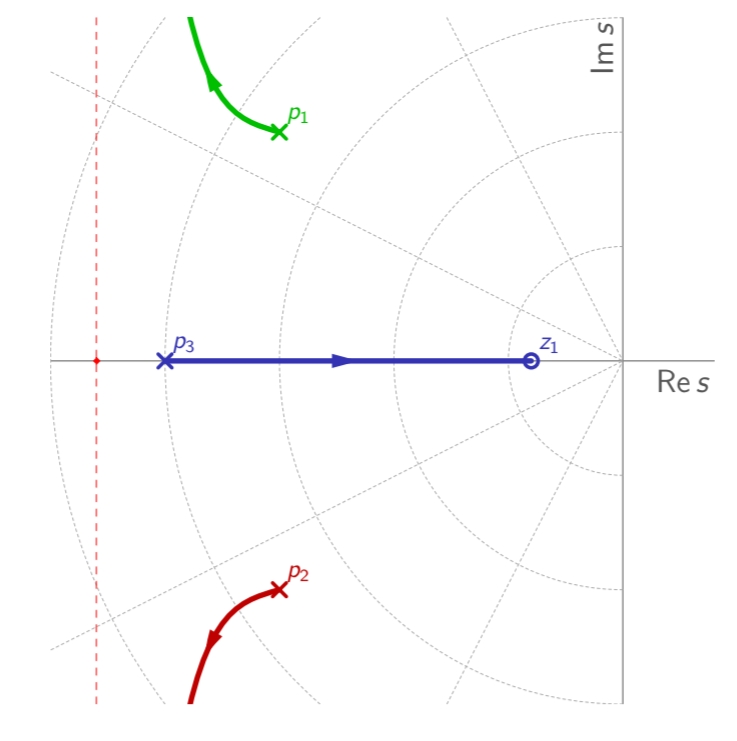
המג”ש המלא. (Leonid Mirkin’s Homepage, n.d.).

תרגילים

תרגיל 1

הביטו במערכת משוב יחידה הבאה:

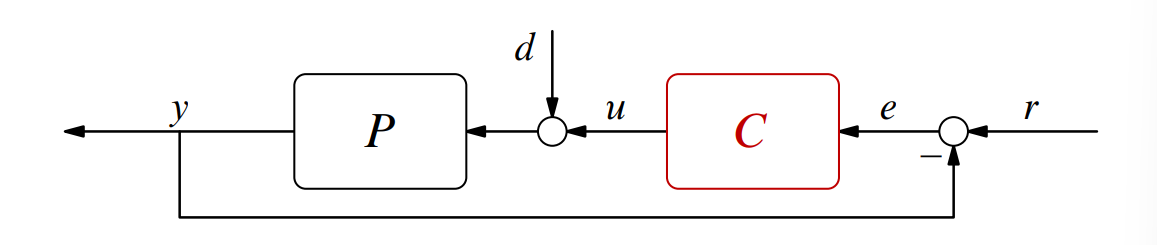
שרטטו באופן איכותי את המג”ש של המערכות הבאות ביחס להגבר .

סעיף א’

פתרון:
נפעל לפי אלגוריתם שרטוט המג”ש.
נביט בפולינום האופייני:

הייצוג מג”ש שלו:

ישנם שלושה קטבים ואפס יחיד, כולם על הציר הממשי. משמאל לאפס נוכל כבר לשרטט ענף שמתחיל ב- .

נמצא כי מרכז הכובד הוא:

והזוויות של האסימפטוטות הן:

התוצאות מוצגות בגרף מג”ש הבא:

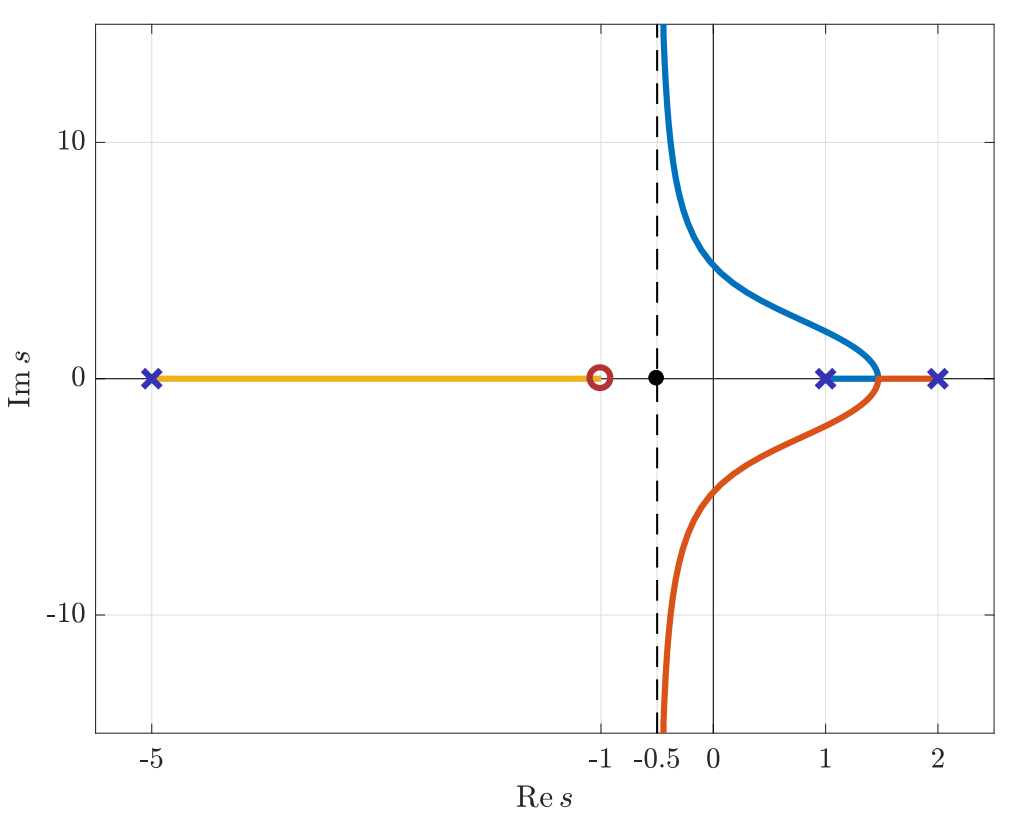
גרף מג”ש עבור המערכת הנתונה. (Leonid Mirkin’s Homepage, n.d.).

נשים לב שעבור גדול מספיק המערכת יציבה, מה שלא נכון עבור המערכת בחוג פתוח (כאשר ).

סעיף ב’

פתרון:
הייצוג מג”ש:

מצאנו שישנם שני אפסים ושני קטבים. מבחינת נקודות הסתעפות על הציר הממשי:

נמצא מתי הנגזרת מתאפסת:

קיבלנו שישנם שתי נקודות הסתעפות על הצד החיובי של הציר הממשי, מה שאומר שלא ניתן לייצב את המערכת!

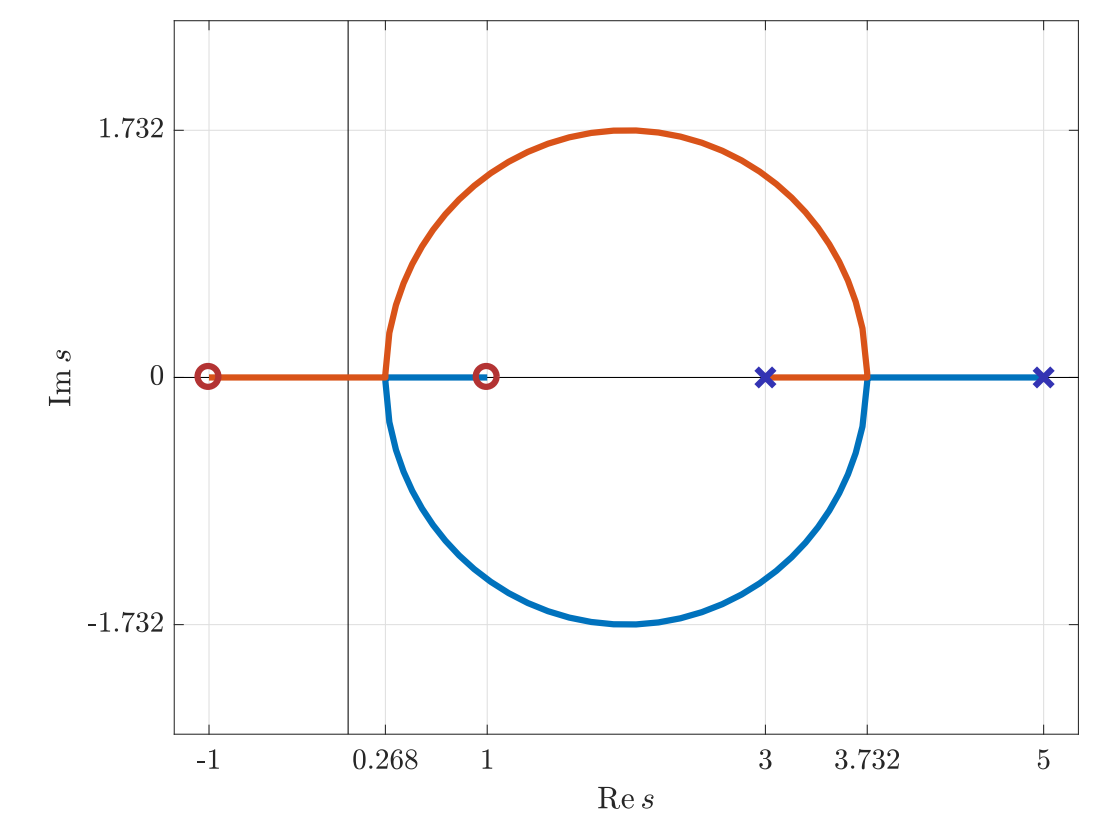
גרף מג”ש עבור המערכת הנתונה. (Leonid Mirkin’s Homepage, n.d.).

כפי שניתן לראות מהגרף, עבור כל שנבחר, תמיד יהיה קוטב אחד ב-RHP.

סעיף ג’

פתרון:
הייצוג מג”ש:

יש שלושה קטבים ב- ואחד ב- , ואפס אחד ב- ולכן על הציר הממשי יש ענפים ב- וב- .

מאחר ו- , ישנם שלושה אסימפטוטות היוצאות ממרכז המסה:

זוויות האסימפטוטות:

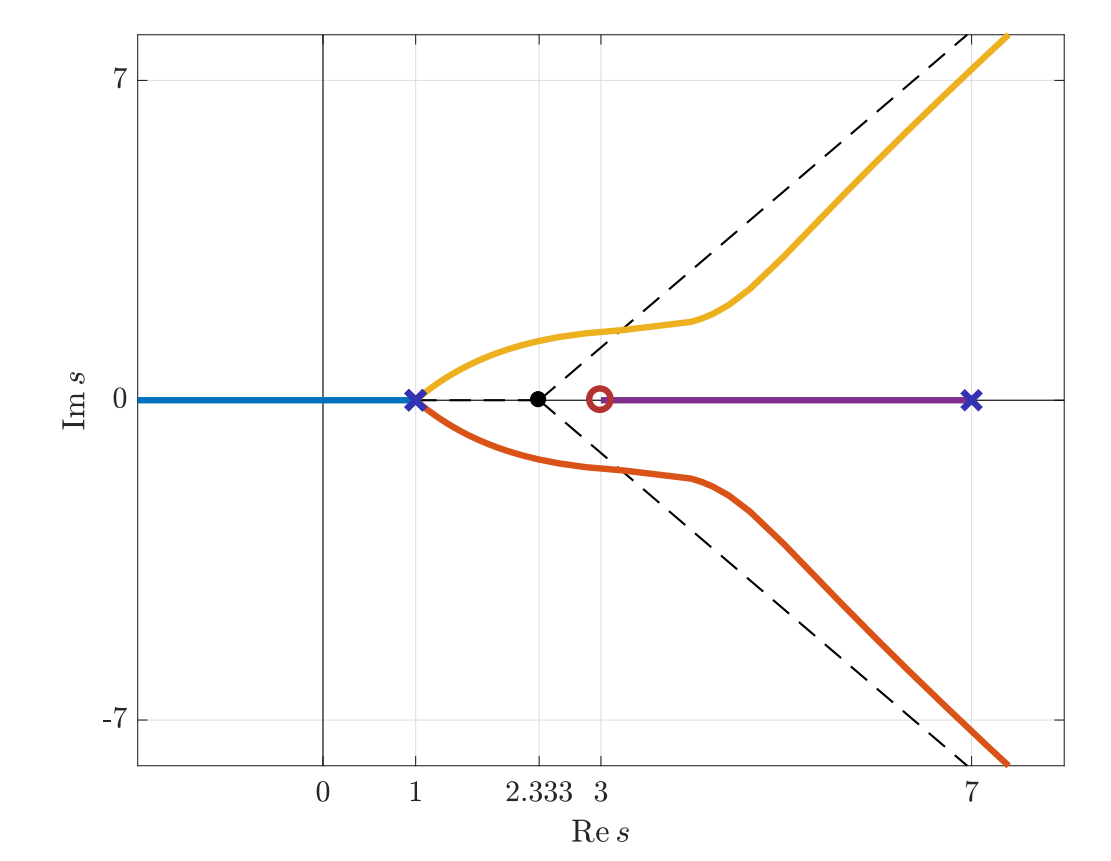
גרף מג”ש עבור המערכת הנתונה. (Leonid Mirkin’s Homepage, n.d.).

שוב, אנו רואים שלפחות שלושה קטבים של החוג הסגור יישארו ב-RHP לכל .

סעיף ד’

פתרון:
הפולינום האופייני במקרה זה הוא:

ולכן הייצוג מג”ש:

ישנם שלושה קטבים - אחד ב- , והשניים האחרים ב- , ולכן יש ענף על הציר הממשי ב- .
מאחר ו- , ישנם שלושה אסימפטוטות:

נקודת ההסתעפות:

נסיק ששניים מתוך שלושת הענפים (אחד כבר הולך ל- על הציר הממשי) מתחילים ב- ובשלב מסוים חותכים את הציר המדומה. חיתוכים אלו מתרחשים בנקודות , כאשר נמצא ע”י:

נקבל את הגרף:

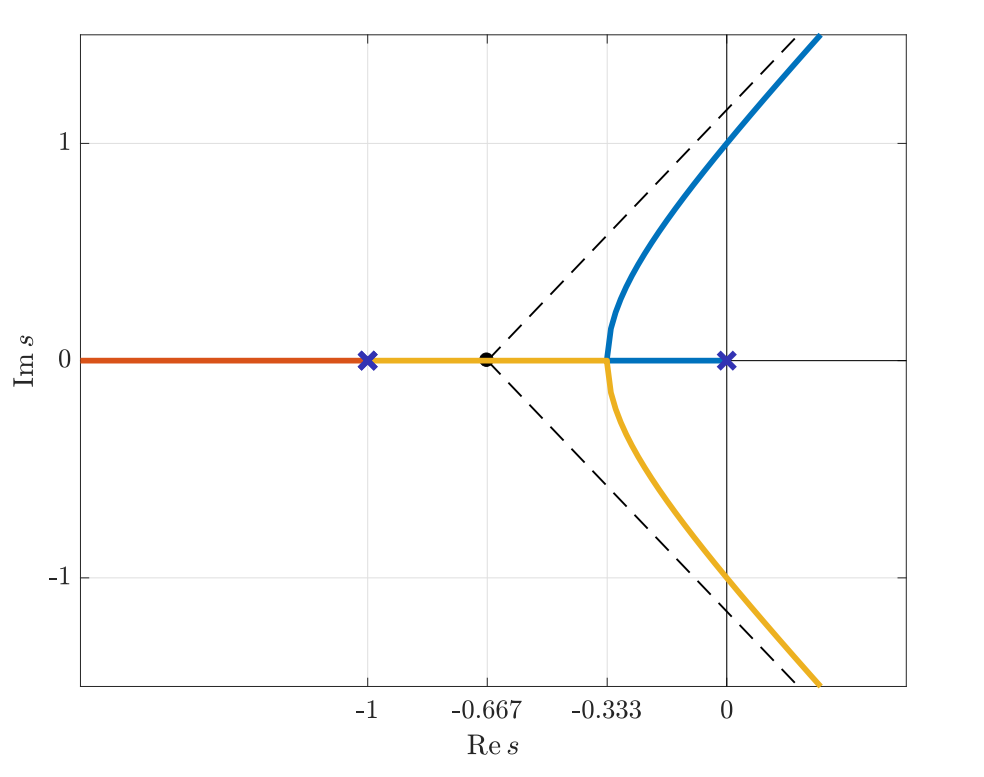
גרף מג”ש עבור המערכת הנתונה. (Leonid Mirkin’s Homepage, n.d.).