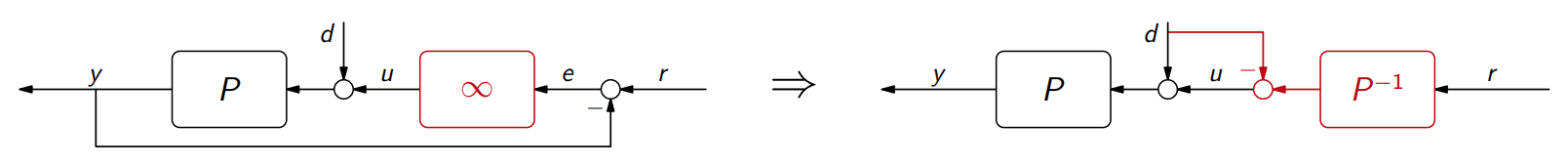ICT1_005 מבוא למשוב

מבוא (תמים) למשוב

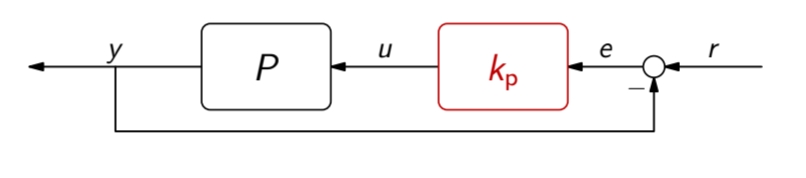
משוב יחידה

יהי אות הניתן למדידה. נביט בבקר הבא:

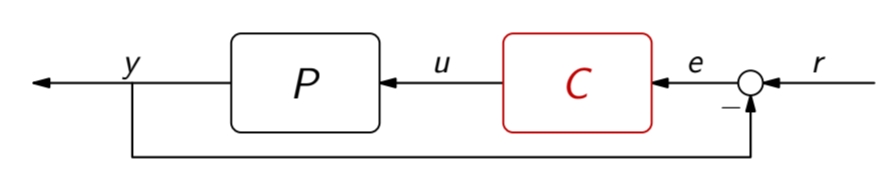
בסכמה זו האות המבוקר נוצר כתוצאה מה-חוסר התאמה בין ואות הייחוס . חוסר התאמה זה מסומן ב-. למבנה בקר זה אנו קוראים משוב יחידה, והוא השיטת בקרת משוב הכי בסיסית.
מהתרשים לעיל נסיק כי:

מאחר וגם ו-, נוכל לרשום גם:

לכל אחד מהתהליכים הבאים ניתן שמות:

ל- אנו קוראים רגישות הבקר (control sensitivity), ל- קוראים הרגישות המשלימה (complementary sensitivity), ול- קוראים הרגישות (sensitivity).
נניח מעתה ואילך ש- ו- הם proper. נאמר שהמחוג מוגדר היטב אם .

ניתן לחשוב

• על כמקביל ל- מבקרה בחוג פתוח.
• על כמקביל ל- מבקרה בחוג פתוח.

דוגמה: בקר סטטי בהגבר גבוה

נשים לב שאם נבחר עבור הגבר מסוים :

אז:

נשים לב שאם , אז , שזה כמעט זהה ל- מבקרה בחוג פתוח. יצרנו פה היפוך תהליך בבקרה בחוג סגור, רק שהפעם, המבקר שלנו לא תלוי ב-.

השפעת הפרעות

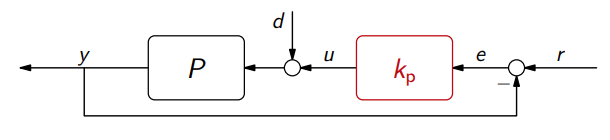
כעת נניח שיש הפרעה במערכת:

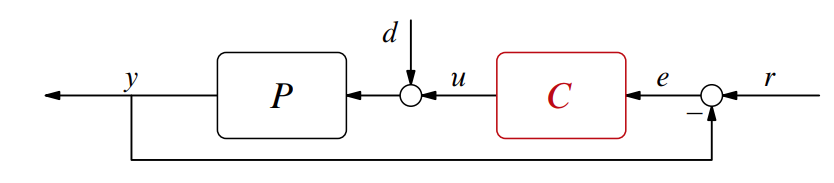
כעת התווסף לנו עוד תהליך במערכת:

ל- אנו קוראים רגישות הפרעה.

ארבעת המערכות ו-, הידועים ככנופיית הארבעה (Gang of Four), מגדירים באופן מלא את המאפיינים של מערכת מבוקרת בחוג סגור.

דוגמה: בקר סטטי בהגבר גבוה והפרעות

נבחר שוב עבור הגבר מסוים :

אז:

נשים לב שאם , אז , שבעצם אומר ש- , ואז, שוב, . אז, בערך אפשר לומר ש

למרות שבמשוב אנו לא מודדים (ישירות) את ההפרעה.

רעש מדידה

כאשר אנו מודדים אות מסוים, אין סיכוי שלא יתווסף למדידה עצמה מידה מסוימת של רעש, אותו נסווג כרעש מדידה . נוכל למדל אותו לתוך המערכת בצורה הבאה:

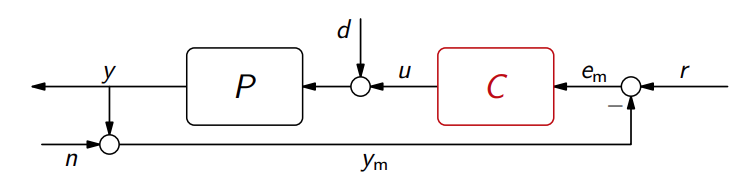
האות החדש מקושר באופן הבא:

נוכל לסכם את ההשפעות של כלל האותות כניסה באופן הבא (צריך לזכור את זה למבחן):

דוגמה:

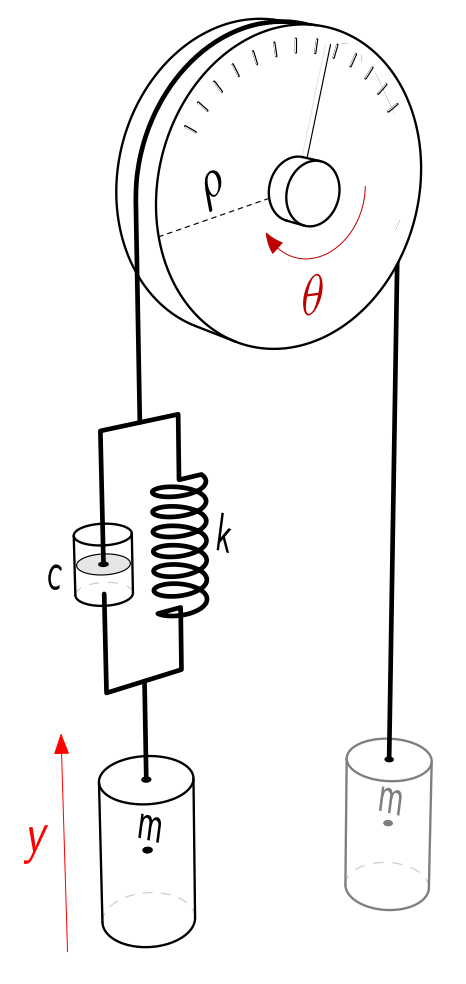
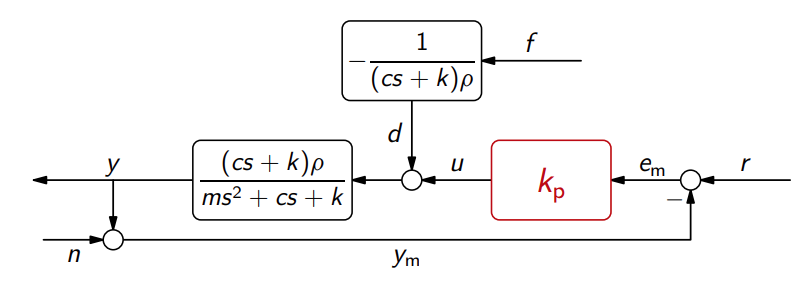
נתונה המערכת הבאה:

עם הבקר בחוג סגור הבא:

נביט בתגובות של מערכת זו עבור .

בבקר בחוג סגור לעיל, הבקר לא תלוי במסה (הוא פשוט ):

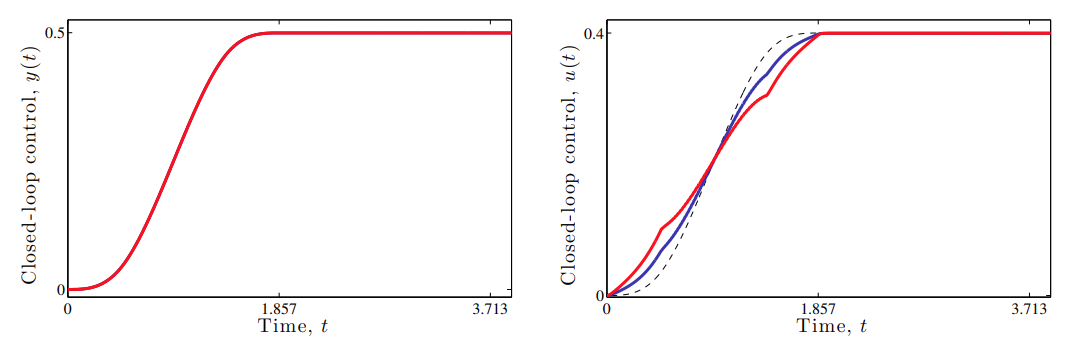
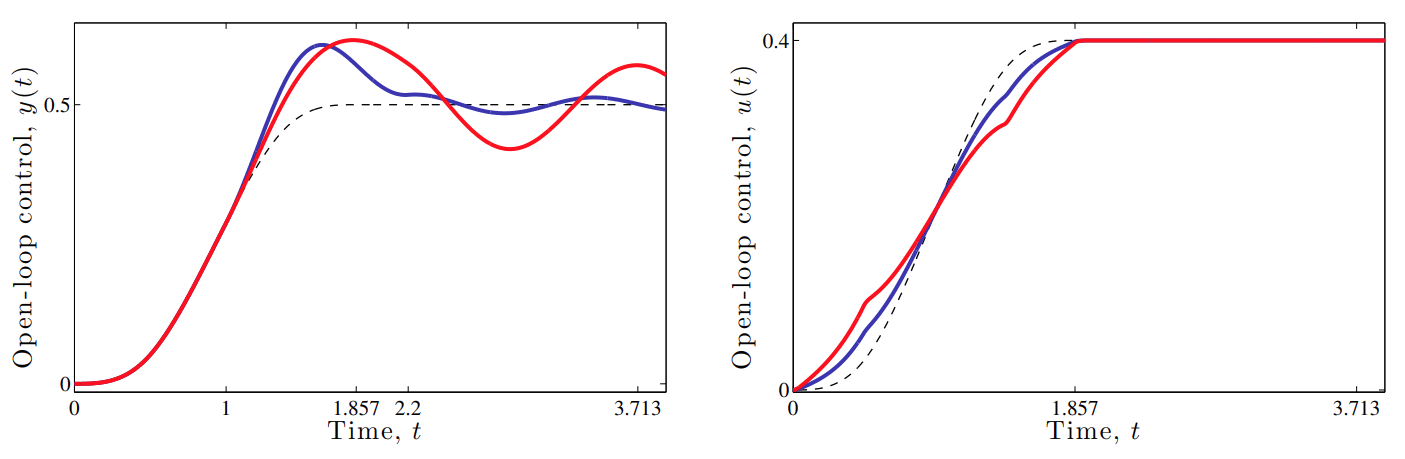
תגובה של הבקר בחוג סגור עבור . הגרף האדום הוא עבור מסה פי יותר גדולה מהמסה של הגרף הכחול. (Leonid Mirkin’s Homepage, n.d.).

לעומת זאת, בבקר בחוג פתוח, אם נרצה לבחור בבקר טוב, הוא חייב להיות תלוי ב-:

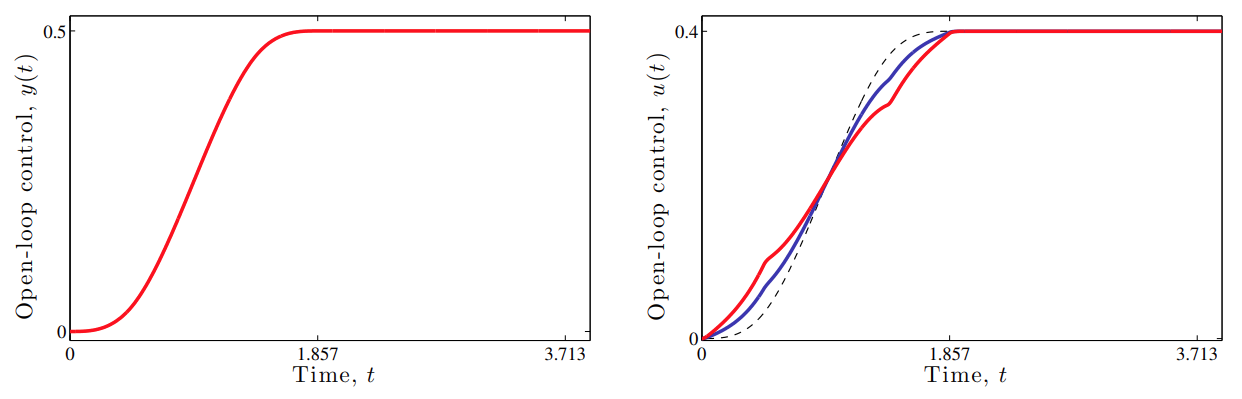
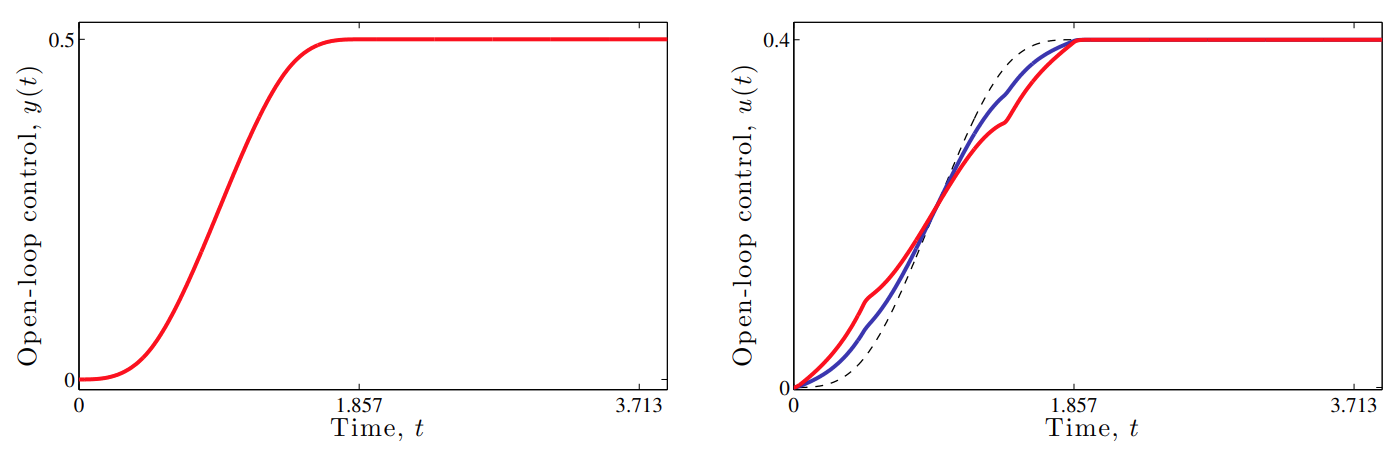
תגובה של בקר בחוג פתוח עבור . (Leonid Mirkin’s Homepage, n.d.).

בבקר בחוג סגור, הבקר רגיש ל- דרך :

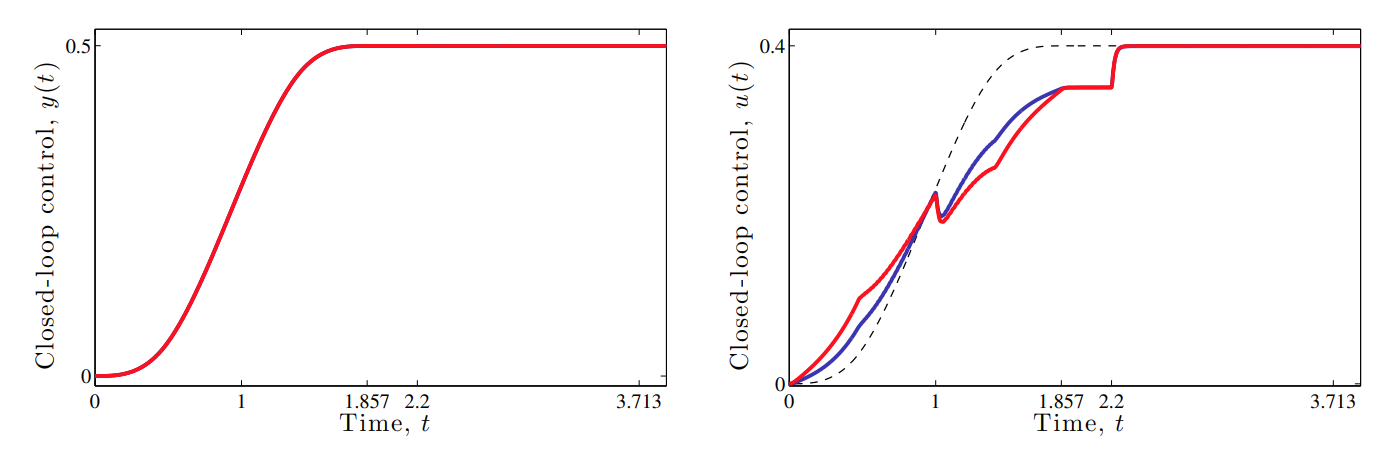
תגובה של הבקר בחוג סגור עבור . (Leonid Mirkin’s Homepage, n.d.).

לעומת זאת, בבקר בחוג פתוח, הבקר “לא מודע” בכלל ל-:

תגובה של בקר בחוג פתוח עבור . (Leonid Mirkin’s Homepage, n.d.).

בבקר בחוג סגור, הבקר רגיש ל-:

תגובה של הבקר בחוג סגור עבור . (Leonid Mirkin’s Homepage, n.d.).

לעומת זאת, הבקר בחוג פתוח לא מושפע בכלל מ-:

תגובה של בקר בחוג פתוח עבור . (Leonid Mirkin’s Homepage, n.d.).

יציבות פנימית

בעוד בקרה בחוג סגור יכולה לעשות מה שבקר בחוג פתוח לא יכול אף לעשות;

• לעבוד גם אם יש שגיאות במידול .
• לעבוד גם במקרה של הפרעות.

לבקר בחוג סגור יש בעיה אחרת: הוא דורש יציבות מכל תהליך בין שני אותות כדי לתפקד טוב.

הגדרה: יציבות פנימית

נאמר שהמערכת בחוג סגור

היא יציבה פנימית אם הפונקציות תמסורת מכל הכניסות האפשריות לכל היציאות האפשריות הן יציבות.

עבור המערכת לעיל, ישנם ארבעה פונקציות תמסורת כאלו - כנופיית הארבעה:

לכן, נצטרך לבדוק רק את ארבעתם (תאכלס, רק שלושה, כי יציב אמ”ם יציב).

כדי לנסות לפשט את הקריטריון ליציבות פנימית, נבחן יותר את הקשרים בין פונקציות תמסורת אלו. נסמן:

נניח ש- ו- הם proper, כאשר שניהם מצומצמים עד הסוף (אין שורשים בשבר עצמו שעדיין לא צומצמו). במקרה זה, נוכל לרשום:

כאשר:

והוא נקרא הפולינום האופייני של המערכת.
לפונקציות תמסורת אלו יש את אותו המכנה, , אלא אם כן יש צמצומי קטבים/אפסים בין הקטבים שלהם ל-.

• אם אין צמצומים, אז לכל הפונקציות תמסורת אותם הקטבים ונוכל לומר שהמערכת יציבה אם הוא Hurwitz.
• אם יש צמצומים, אז יש איזשהו שטאנץ (שניר יא אשכנזי) שמוסבר סבבה יחסית במצגות, והוא מוביל למשפט הבא:

משפט:

אם ו- הם proper וגם , אז המערכת יציבה פנימית אמ”ם:

1. אין צמצומים לא יציבים בין ו-.
2. אחת מהמערכות בחוג סגור יציבה.

במובנים של פולינום אופייני:

משפט:

אם ו- הם proper ו- , אז המערכת היא יציבה פנימית אמ”ם לפולינום האופייני אין שורשים במישור הימני הסגור (RHP).

תרגילים

תרגיל 1

תהליך עם הפונקציית תמסורת:

מבוקר ע”י משוב יחידה עם בקרים סטטיים (פרופורציונליים) מהצורה .

סעיף א’

מצאו את ארבעת הפונקציות תמסורת של מערכת זו. מהו הפולינום האופייני? תחת אלו הגברים המערכת במחוג סגור היא יציבה פנימית?

פתרון:
מהגדרת , כבר נוכל לומר ש:

נחשב כל אחד מארבעת פונקציות התמסורת:

כדי לבדוק את היציבות אנו צריכים להביט במכנה. נזכור מטבלת רות שיש דרך מהירה לבדוק Hurwitz עבור פולינום ממעלה שלישית, ונסיק כי כדי שהמכנה יהיה Hurwitz, צריך להתקיים:

סעיף ב’

יהי . שרטטו את התגובות של כל מערכת בחוג סגור למדרגת יחידה. הסבירו את השוני בין התגובות לערכים שונים של .

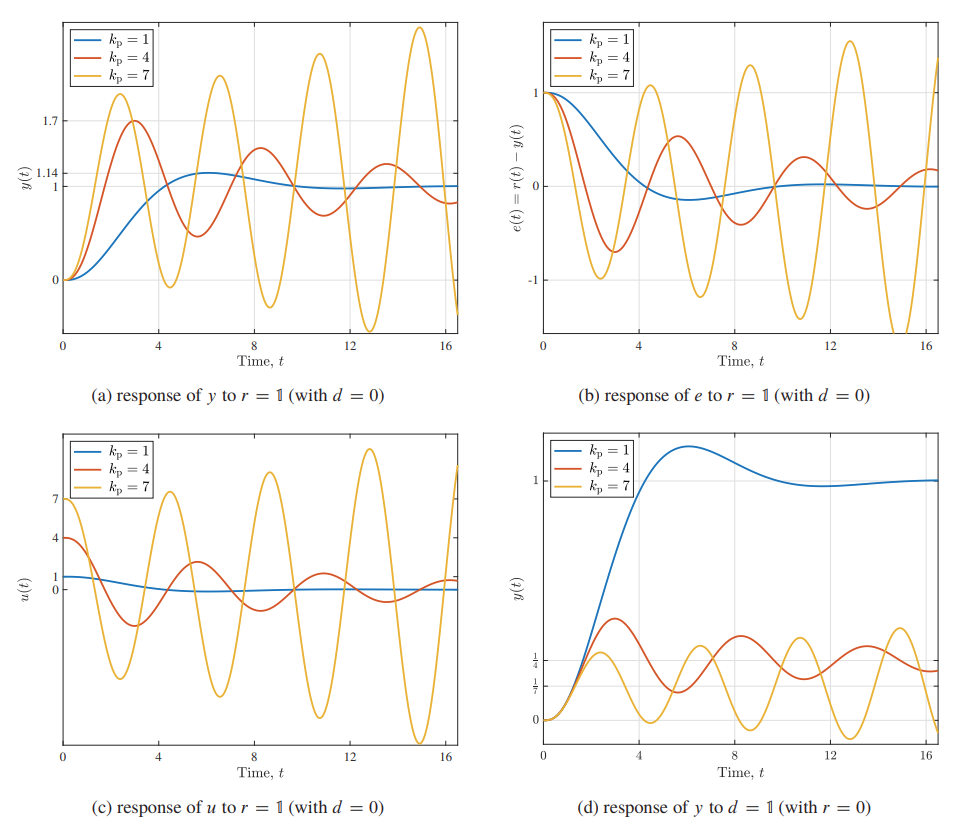
תגובות מדרגה של מערכת בחוג סגור.

תרגיל 2

הביטו במערכת הבאה:

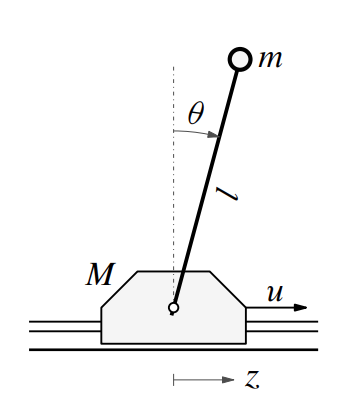
מטוטלת הפוכה על עגלה.

המטוטלת ההפוכה כוללת מסה על מוט חסר מסה באורך שמותקן על עגלה במסה . כוח חיצוני פועל על העגלה. משוואות התנועה של מערכת זו הם:

כאשר הוא הזווית של המטוטלת ו- הוא המיקום העגלה. הפרמטרים הם ותאוצת הכבידה .

סעיף א’

בצעו לינאריזציה על המערכת ואת הפונקציית תמסורת שלה עם כקלט ותאוצת העגלה כפלט.

פתרון:

נשים לב שיש לנו 2 משתנים ודרגת הנגזרת הכי גבוה היא . מבחינת משתני מצב יש לנו ארבעה שנסמנם:

לכן משוואות המצב שלנו בצורה מטריצית:

אנו רוצים להעביר הכל לצד ימין, כך שנוכל לרשום את המשוואה באופן:

נסמן:

נראה שנוכל לפתור את התרגיל גם בלי בלחשב את . אבל, כדי אנו עדיין צריכים להוכיח שאפשר בכלל לעשות , כלומר, להוכיח ש- הפיכה. במקרה שלנו, זה לא כזה נורא, אם נזכור ש- הוא מטריצת בלוקים (wtf), ולכן הדטרמיננטה שלה היא פשוט:

לכן אנו בכלל יכולים לרשום:

נתחיל מלמצוא נקודת שיווי משקל:

נסיק כי:

עבור המצב בו המטוטלת למעלה (מה ששאלו), נבחר .
נשים לב גם שאין לנו תנאי על , כך שזה לא משנה איפה המטוטלת נמצאת על הציר. נבחר קבוע כלשהו. לכן נקודת שיווי המשקל שלנו:

נמצא את היעקוביאנים, ונשים לב שזה לא כל כך פשוט:

נוכיח כעת שיש איזשהו טריק עם הגזירה של מטריצה הופכית. אנו יודעים ש:

נגזור:

נציב את זה כעת ב-:

האיבר באמצע מתבטל כי הוא בדיוק , ו- בשיווי משקל (ב-) שווה לאפס, מהגדרת שיווי המשקל. נשארנו עם:

נחשב את :

נציב ב-:

נשים לב גם כי:

לכן המערכת לאחר לינאריזציה:

נעביר אגף:

נחשב את כי אותו אנו יודעים לחשב:

נציב בחזרה במערכת:

בעזרת פיתוח לא רלוונטי, שלא נדרש למבחן, נחלץ ממשוואת מצב זו את הפונקציית תמסורת:

נביט רק בשורה הראשונה:

הביטוי בצד שמאל, הוא למעשה במישור לפלס, כי . מאחר ו- , נוכל לרשום , כך ש:

נציב נתונים ונקבל:

נסמנו כהתהליך שלנו:

סעיף ב’

המערכת נשלטת במשוב יחידה סטנדרטי. האם הוא ניתן לבקרה (כלומר, להתייצב) ע”י הבקר:

וודאו את היציבות גם ע”י הפונקציות תמסורת של ו-, וגם ע”י הפולינום האופייני של המערכת.

פתרון:
נשים לב שיש לנו צמצום לא יציב עם התהליך שיצא לנו בסעיף הקודם. נראה איך זה ישפיע על כנופיית הארבעה:

קיבלנו ש- יש קוטב ב-RHP, , מה שהופך את המערכת שלנו ללא יציבה פנימית. כל הפרעה, משב של רוח קטן, יפיל את המטוטלת שלנו.