מרכז כובד ומרכז מסה
מרכז כובד
נביט בגוף תלת מימדי בעל צורה כללית, ומסה
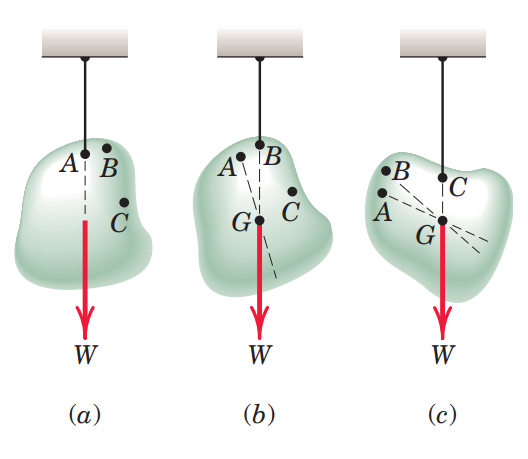
נסמן את קו הפעולה של
הגופים שאנו פוגשים ביום-יום נמצאים קרוב מאוד לכדור הארץ, ומסתם זניחה ביחס אליו. אבל ככל שהגוף יותר גדול, ורחוק יותר מכדה”א, שדה הכבידה שמופעל עליו משתנה - הוא כבר לא אחיד (
כתוצאה מכך, קווי הפעולה של כוחות הכבידה כבר לא מקבילים, ואין מרכז כובד יחיד - אין משמעות למרכז כובד עבור גופים אילו. לכן נניח אנו נעבוד עם גופים שנמצאים תחת שדה כבידה אחיד שנוצר ע”י כדה”א, כך שיהיה לנו מרכז כובד יחיד.
מציאת מרכז כובד עבור גוף יחיד
כדי למצוא מבחינה מתמטית את מרכז הכובד של כל גוף, נחשב את שקול המומנטים בכל ציר (ע”י עיקרון המומנטים). המומנט של הכוח השקול
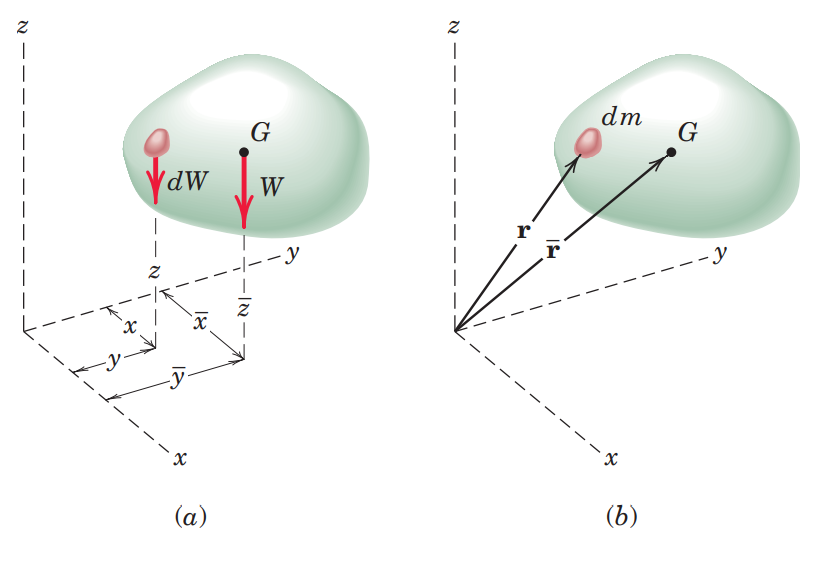
הכוח השקול
נסכום את מומנטים אלו כדי לקבל
באותו אופן, עבור כל שאר הצירים, נקבל:
נוסחה:
הערות:
- נשים לב שהמונה בכל אחד מהביטויים האלו הוא סכום המומנטים, לעומת הכפל
שהוא המומנט של הכוח השקול - והם כמובן שווים.
אם נציב
נוסחה:
או מבחינה וקטורית:
נוסחה:
מציאת מרכז כובד עבור גוף בעל נפח רציף
הצפיפות (
אם
כאשר
אם נרצה לפרק לרכיבים:
נוסחה:
מרכז כובד לעומת מרכז מסה
הנוסחאות הקודמות לא תלויות ב-
זה חסר משמעות לדבר על מרכז כובד של גוף שלא נמצא תחת שדה כבידה, הרי שום כוחות כבידה לא פועלים עליו. לעומת זאת, מרכז המסה של גוף לא תלויה בשדה כבידה בו הוא נמצא, ויש לו חשיבות רבה כאשר אנו רוצים לחשב את התגובה הדינמית של גוף לכוחות לא מאוזנים. אבל זה כבר חומר של סמסטר הבא.
ניזכר בהגדרת מרכז מסה מפיזיקה:
נשים לב שאם נרחיב אותו למקרה של גוף יחיד בעל נפח רציף, נקבל:
שזוהי בדיוק אותה נוסחה שקיבלנו מקודם, כאשר הנחנו כי שדה הכבידה אחיד בגודלו וכיוונו.
מרכז מסה של גוף מורכב
כאשר גוף מסוים ניתן לפירוק למספר חלקים שמרכזי המסה שלהם טריוויאלים לחישוב, אנו נשתמש בעיקרון המומנטים.
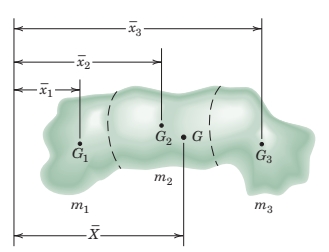
לגוף באיור, יש מסות
כאשר
נוסחה:
דוגמה:
נפרק את הגוף הנתון לחלקים שאנו יודעים את מרכז המסה שלהם:
נבנה טבלה המציגה את כל מרכזי הכובד. נשים לב שכל ה"חורים" מוצגים בסימן שלילי:
ניעזר בנוסחה שבנינו ונסיק כי: