CAL1_001 פונקציה

פונקציה

פונקציה

הגדרה:

בהנתן שתי קבוצות , פונקציה מ- ל- היא התאמה המתאימה לכל איבר ב- איבר יחיד ב-. נסמן פונקציה מ- ל- ע”י . נקראת תחום ההגדרה של , ו- נקראת הטווח של .
את העובדה כי f מתאימה לאיבר את האיבר נסמן ע”י . נאמר כי הוא התמונה של (תחת ) וכי הוא מקור של (תחת ).
התמונה של פונקציה היא קבוצת כל האיברים של המתקבלים מאיברים של . נסמן את התמונה של ע”י או . אז .

פונקציה חח”ע ועל

הגדרה:

נאמר כי פונקציה היא על אם התמונה שלה שווה לטווח שלה, כלומר אם כל איבר ב- מתקבל מאיזשהו איבר ב-, או, באופן שקול, אם .
נאמר כי פונקציה היא חד-חד-ערכית (ב-), או חח”ע, אם לאיברים שונים ב- מתאימים איברים שונים ב-. כלומר אם אז . באופן שקול, אם עבור מתקיים כי , אזי .

פונקציה מונוטונית

הגדרה:

נאמר כי פונקציה מונוטונית עולה, או פשוט עולה, אם כאשר ב-, אז . נאמר כי פונקציה היא מונוטונית עולה ממש אם כאשר אז .
נאמר כי פונקציה מונוטונית יורדת, או פשוט יורדת, אם כאשר , אז . נאמר כי פונקציה היא מונוטונית יורדת ממש אם כאשר אז .
נאמר כי פונקציה מונוטונית אם היא מונוטונית עולה או מונוטונית יורדת.
נאמר כי פונקציה מונוטונית ממש אם היא מונוטונית עולה ממש עו מונוטונית יורדת ממש.

פונקציה חסומה

הגדרה:

נאמר כי היא חסומה מלמטה אם קיים מספר כך ש- לכל .
נאמר כי היא חסומה מלמעה אם קיים מספר כך ש- לכל .
נאמר כי היא חסומה אם היא חסומה מלמעלה ומלמטה, כלומר אם קיימים מספרים כך ש- לכל . המספר נקרא חסם מלמטה, והמספר נקרא חסם מלמעלה. מושגים אלו גם מתאימים לקבוצות, ואפילו יותר טבעיים שם.

הערות:

1. התכונות חח”ע, מונוטוניות, חסימות הן תכונות של הפונקציה על תחום ההגדרה ולא תכונה של נקודה.

פונקציה זוגית ואי זוגית

הגדרה:

נאמר כי פונקציה היא זוגית אם היא מוגדרת על קבוצה סימטרית ביחס לראשית (כלומר נמצא בקבוצה אמ”ם נמצא בקבוצה), וגם לכל בקבוצה.
נאמר כי היא אי זוגית אם היא מוגדרת על קבוצה סימטרית ביחס לראשית, וגם לכל בקבוצה.

פונקציה מחזורית

הגדרה:

נאמר כי פונקציה היא מחזורית אם קיים מספר שונה מאפס עבורו לכל .

פעולות על פונקציות

פעולות אריתמטיקה בסיסיות

הגדרה:

יהיו פונקציות. נגדיר את הפעולות האריתמטיות על הפונקציות:

הרכבה של פונקציות

הגדרה:

בהנתן ו-, ההרכבה מוגדרת ע”י:

דוגמאות:

1. אם , אז:

נשים לב כי תחום ההגדרה של הוא כל ה- עבורם אי שלילי. לעומת זאת:

ותחום ההגדרה של פונקציה זו הוא .

פונקציות אלמנטריות

פונקציה רציונאלית

הגדרה:

פונקציה רציונלית היא פונקציה שהיא מנה של פולינומים, כלומר כאשר ו- פולינומים.
תחום ההגדרה של הוא הישר הממשי חוץ מהנקודות בהן המכנה מתאפס. אם אז יש לכל היותר נקודות בהן הפונקציה אינה מוגדרת.

פונקציה מעריכית (אקספוננציאלית)

הגדרה:

עבור קבוע (), הפונקציה המעריכית אם בסי היא . הקבוע נקרא הבסיס ו- נקרא המעריך או האקספוננט.

הערות:

1. הפונקציה המעריכית עולה ממש כאשר ויורדת ממש כאשר .
2. תחום ההגדרה של הפונקציה המעריכית הוא כל הישר .
3. התמונה של הפונקציה המעריכית היא הקרן .

פונקציה טריגונומטרית

הגדרה:

פונקציה מהסוג , כאשר ברדיאנים נקראת פונקציה טריגונומטרית.

פונקציה הפוכה

הגדרה:

אם היא פונקציה חח”ע ועל, אז לכל קיים יחיד עבורו . הפונקציה ההפוכה ל-, שתסומן ע”י , היא הפונקציה מ- ל- המתאימה לכל את ה- היחיד עבורו .

נשים לב כי ו:

בנוסף:

נמנה מספר פונקציות הפוכות:

פונקציות ההפוכות לפולינומים

לא כל פולינום הוא חח”ע ועל ולכן נסתכל רק על תחום בו הפונקציה חח”ע כאשר הטווח הוא התמונה של התחום. למשל, אינה חח”ח על כל הישר, אבל אם נגביל את תחום ההגדרה לאי-שליליים ואת הטווח לאי-שליליים אז נקבל פונקציה שהיא חח”ע ועל:

הפונקציה ההכפוכה לפונקציה זו היא פונקציית השורש :

פונקציה לוגריתמית

לכל הפונקציה המעריכית היא חח”ע ועל ולכן הפיכה. נסמן את הפונקציה ההופכית ע”י .

פונקציה טריגונומטרית הפוכה

הפונקציה היא חח”ע ועל בקטע והתמונה שלה היא . אבל גם על הקטע היא חח”ע. יש אינסוף קטעים באורך עבורם היא חח”ע.
הבחירה הסטנדרטית היא . בקטע זה פונקציית הסינוס היא עולה ממש. הפונקצייה ההפוכה לה היא:

באותו אופן נוכל לעשות לפונקציות .

פונקציה אלמנטרית

הגדרה:

פונקציה היא פונקציה אלמנטרית אם ניתן לבנות אותה ע”י מספר סופי של פעולות האריתמטיקה הבסיסיות והרכבה ממספר פונקציות בסיסיות:

1. פולינום
2. פונקציה רציונאלית
3. פונקציה מעריכית
4. פונקציה טריגונומטרית

בנוסף, כל פונקציה הופכית של פונקציה אלמנטרית, היא פונקציה אלמנטרית.

הערות:

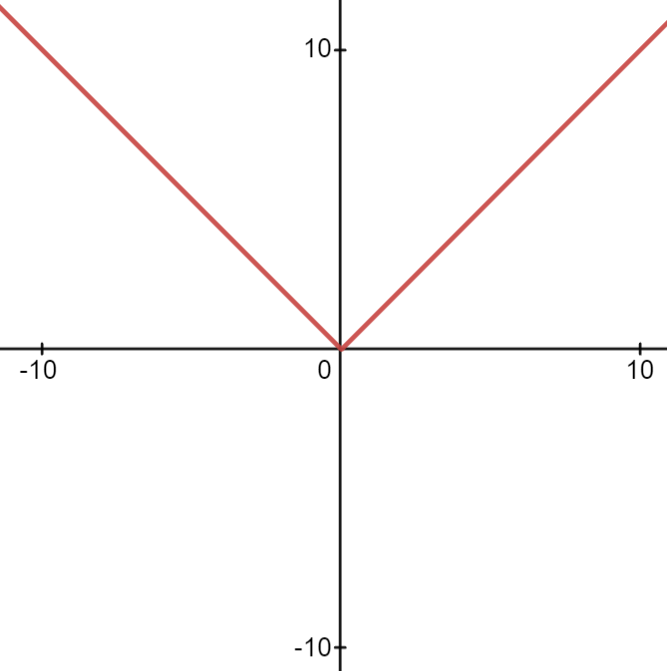
פונקציית הערך המוחלט היא פונקציה אלמנטרית מכיוון ש-, כלומר היא הרכבה של פונקציית השורש (שהיא אלמנטרית כי היא הופכית של הפונקצייה ), עם הפונקציה .

לעומת זאת, הפונקצייה:

אינה אלמנטרית.
2. אם פונקציות אלמנטריות אז גם פונקציה אלמנטרית עם תחום הגדרה שהוא כאשר מוגדר וגם . למה? כיוון ש- אלמנטרית אז גם אלמנטרית כהרכבה של אלמטריות, כאשר תחום ההגדרה הוא כאשר . לכן אלמנטרית כי מכפלה של אלמנטריות, ותחום הגדרה שהוא כאשר מוגדר וגם . לבסוף אלמנטרית כהרכבה של אלמנטריות.
אבל:

ולכן פונקצייה אלמנטרית עם תחום הגדרה שהוא כל ה- עבורם מוגדר וגם . כמסקנה נקבל כי לכל מספר ממשי הפונקצייה היא אלמנטרית עם תחום הגדרה . (זה לא מובן מאליו, במקרה זה הוא לא פולינום, הרי יכל להיות מספר לא שלם או אפילו שלילי).