שאלה 1
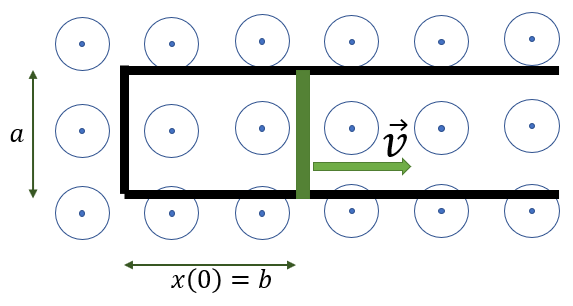
סכימת המוט על המסגרת
מדוגמה על תיל בשדה מגנטי, אנו יודעים כי:
שאלה 2
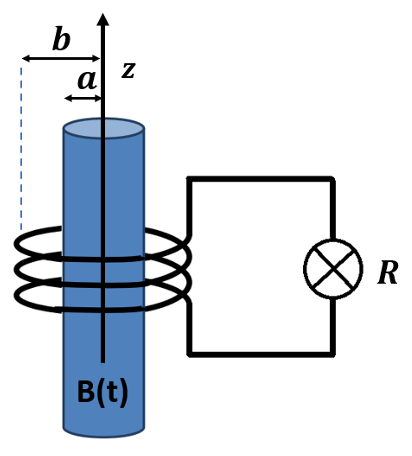
סכימת הגליל
השדה המגנטי בגליל משתנה בזמן, כך שהשטף דרך שלושת הסלילים משתנה בזמן. מאחר וגם השדה המגנטי שורר רק ב-
לכן, לפי חוק פאראדיי:
לכן, הזרם החשמלי דרך הנורה (לפי חוק אוהם):
שאלה 3
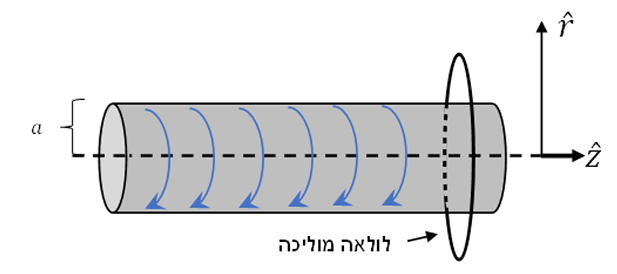
סכימת הלולאה
בלולאה המוליכה, הזרם המושרה של הלולאה נתון ע”י חוק אוהם:
כאשר
לכן:
נרצה למצוא את השטף המגנטי דרך הסליל. את הגליל נושא זרם נוכל להקביל למקרה של גליל אינסופי מסתובב, רק הפעם
כדי למצוא את השדה החשמלי, ניעזר בחוק אמפר.
לולאת אמפר שנמצאת חלקית בתוך הגליל.
מסימטריה, מבין 4 צלעות המלבן, רק הצלע האנכית הפנימית תורמת לאינטגרל (בחוץ השדה אפס, בצלעות אופקיות המסלול מאונך לכיוון השדה
נחשב את
לפי חוק אמפר:
נשים לב שביטוי זה נכון רק עבור
נשים לב ש-
ולכן הזרם המושרה (מבקשים את הגודל, אז נוריד את הסימן מינוס):
שאלה 4
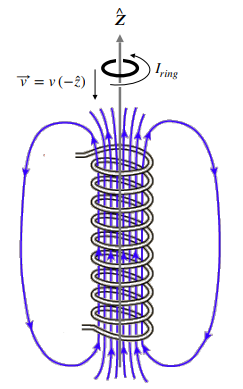
סכימת הסליל
בתחילת התהליך, מאחר והשדה המגנטי חלש יותר בבסיסים, השטף המגנטי בתוך הטבעת עולה, ולכן לפי חוק לנץ נוצר בו זרם המתנגד לשינוי בשטף המגנטי - עם כיוון השעון.
בסוף התהליך, כאשר הטבעת יוצאת מהסליל, נקבל את התופעה ההפוכה.
שאלה 5
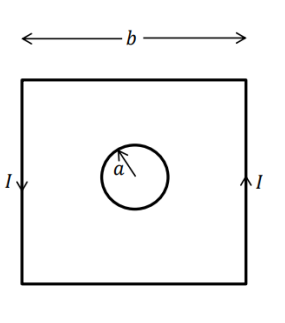
סכימת הטבעת
הזרם שבמסגרת הריבועית יוצר שדה מגנטי בתוכו, בכיוון החוצה מהמסך (כי נתון שהזרם נגד כיוון השעון). לפי שאלה 4 בגיליון קודם, גודל שדה זה במרכז הוא (כאשר נשים לב שכאן מדובר בריבוע):
נניח כי גודל זה לא משתנה משמעותית בתוך הטבעת המוליכה, הרי נתון
מאחר ו-
לכן, לפי חוק פאראדיי:
ולכן הזרם:
הסימון השלילי על הכא”מ מעיד על כך שהזרם המושרה בכיוון לתוך המסך, כלומר מסתובב עם כיוון השעון.
שאלה 6
לפי אנרגיה במשרן:
נציב נתונים ונקבל:
שאלה 7
במעגל RL, בחיבורו למקור מתח, הזרם נתון ע”י:
ערכו באינסוף הוא
לפי אנרגיה במשרן, שהוא בעצם האנרגיה האגורה בשדה המגנטי:
ברגע הנתון:
שאלה 8
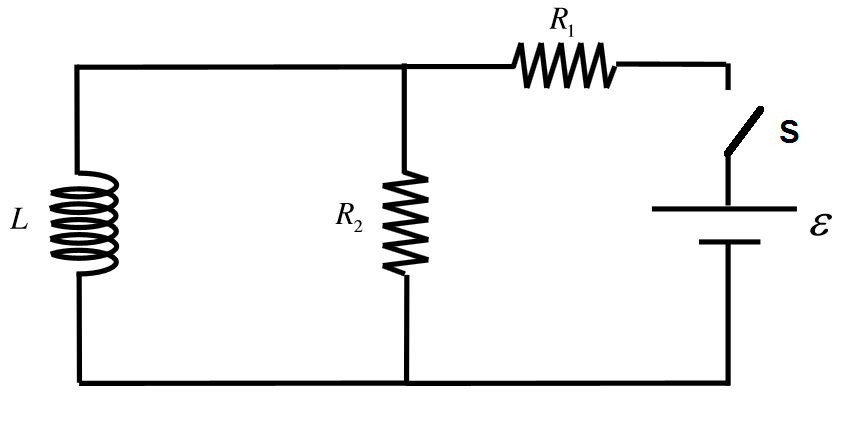
סכימת המעגל
סעיף א’
מיד לאחר סגירת המפסק, התיל מתפקד כמו נתק, כך שהמעגל השקול הוא שני נגדים מחוברים בטור. ההתנגדות של שניהם:
ולכן הזרם דרך נגד
נציב נתונים ונקבל:
סעיף ב’
לאחר זמן רב מאוד, הסליל מתפקד כמו קצר, כך שהזרם יעבור דרכו ולא יעבור בכלל דרך
סעיף ג’
לאחר זמן רב מאוד, מאחר והסליל מתפקד כמו קצר, הפרש הפוטנציאלים בו הוא פשוט
סעיף ד’
כאשר פותחים מחדש את המפסק, הזרם דרכו הוא עדיין הזרם
נציב נתונים ונקבל:
סעיף ה’
כאשר המפסק פתוח, רק הסליל ו-
נציב את הפתרון מסעיף קודם ואת
שאלה 9
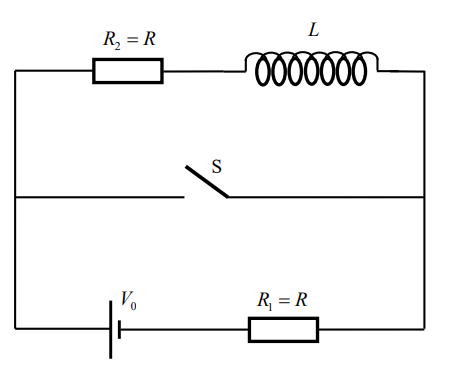
סכימת המעגל
כאשר המפסק היה פתוח, הזרם על הסליל היה (הסליל תפקד כמו קצר, אז זה כמו חיבור נגדים בטור):
לאחר הרבה זמן, אנו יודעים שהסליל יתפקד כמו קצר, כך שהזרם יעדיף לעבור רק דרך המפסק, ואז המעגל האפקיטיבי יהיה פשוט מקור המתח והנגד
ישנם רק שני פתרונות המקיימים את תנאים אלו:
ההבדל היחיד בין שני הפתרונות הוא שהם מייצגים קצבי גדילה שונים לזרם. כלומר, עלינו להחליט בין
שאלה 10
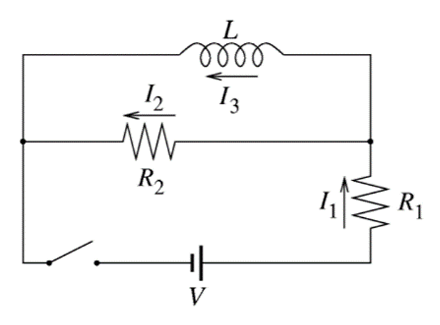
סכימת המעגל
לאחר זמן רב, הסליל מתפקד כמו קצר, כך שאין זרם דרך הנגד