PHY2_HW009 גיליון בית 9

שאלה 1

לפי דוגמה על שני תילים, הכוח ליחידת אורך:

נציב פרמטרים ונקבל:

שאלה 2

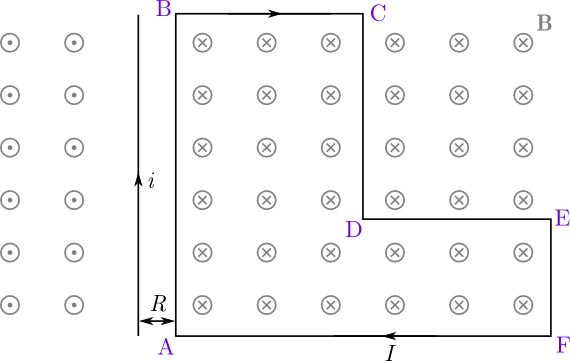
סכימת המסגרת

סעיף א’

לפי שדה מגנטי של תיל אינסופי:

לפי כוח מגנטי הפועל על זרם, על פועל הכוח:

נשים לב כי בכיוון , ו- בכיוון , ולכן המכפלה הוקטוריות בינהם תהיה בכיוון . בנוסף, שינוי קטן הוא פשוט שינוי קטן :

נציב נתונים ונקבל:

סעיף ב’

באותו אופן כמו סעיף קודם, נקבל:

נציב נתונים ונקבל:

שאלה 3

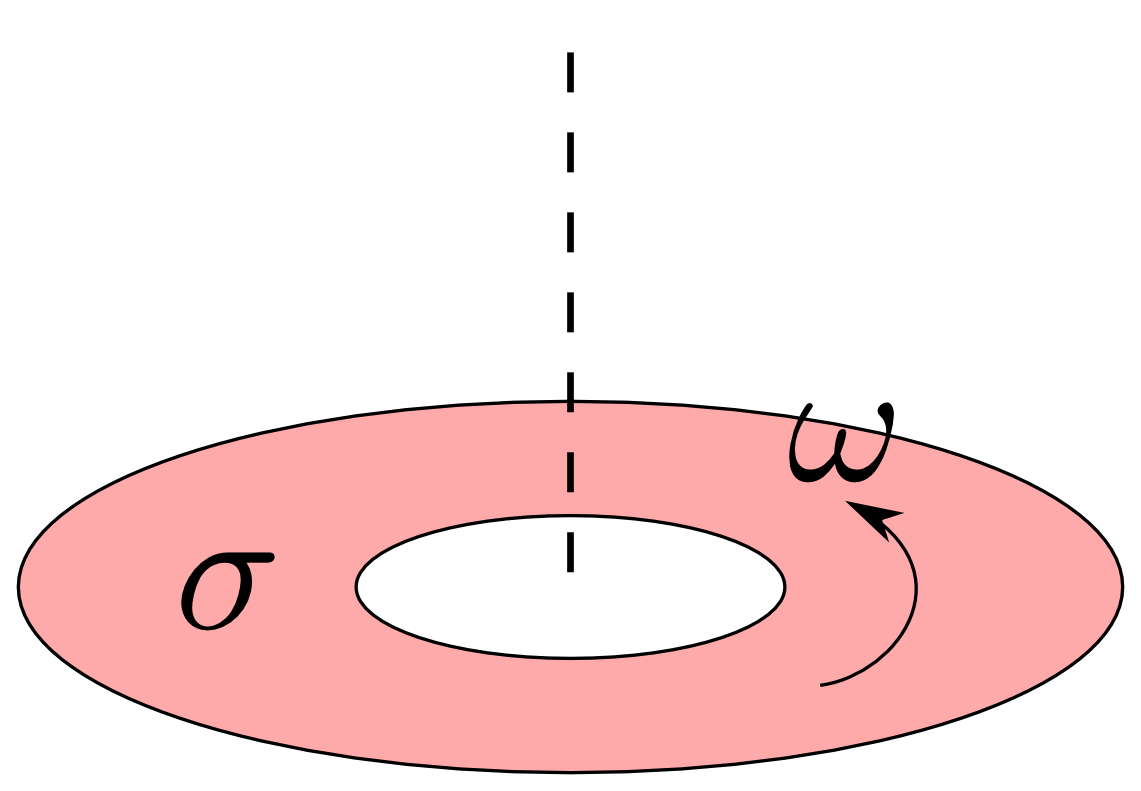
סכימת הדסקה

סיבוב הדסקה שקול לזרימה באוסף טבעות ברדיוסים מ- ל-.
משדה מגנטי של טבעת זרם בציר המרכזי:

נשים לב שהזרם תלוי ב-:

בתנועה מעגלית, . נתון גם כי , ולכן:

לכן, עבור טבעת ברדיוס :

נציב ב-:

נסכום את כל הטבעות לקבלת דסקה:

לפי אינטגרלים שימושיים:

נציב נתונים ונקבל:

שאלה 4

סכימת הלולאת זרם

משדה מגנטי של תיל סופי, במקרה בו הנקודה שאנו רוצים לחשב נמצאת באמצע התיל:

כאשר הוא המרחק מהתיל. נסכום את גודל זה ארבע פעמים - פעמיים עבור צלעות ופעמיים עבור צלעות , כאשר נשים לב שעבור צלעות מקבילות, הזרם באותו הכיוון (לתוך המסך) ובאותו הגודל.

נציב נתונים ונקבל:

שאלה 5

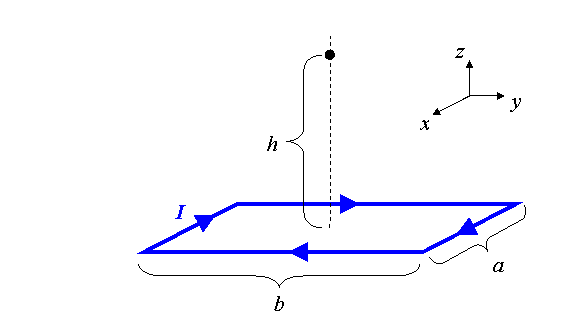
סכימת הלולאה

נשים לב שמקרה זה כמעט זהה לשאלה 4, אבל הפעם:

כאשר הוא המרחק מהתיל, ומרחק המרכז מכל אחד מהתילים הוא:

להבדיל משאלה קודמת, השדה המגנטי בנקודה הדרושה מכל אחד מהתילים, בכיוון שונה:

השדה המגנטי שכל תיל מפעיל פועל בניצב לוקטור מיקום הנקודה.

מסימטריה נסיק כי סך השדה המגנטי פועל רק בכיוון , ולכן נצטרך להטיל כל כח לכיוון זה.
נשים לב כי:

אז למשל עבור , שהוא שדה מגנטי שנוצר כתוצאה מצלע , בכיוון , נקבל:

באותו אופן, נקבל עבור הצלע השנייה באורך :

ולכן, סך השדה המגנטי בכיוון (נכפיל פי , כי סך הכל יש 2 צלעות מכל סוג):

נציב נתונים ונקבל:

שאלה 6

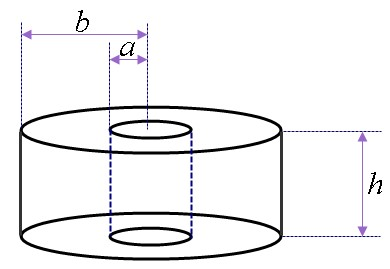
סכימת הטורוס

נבחר לולאת אמפר מעגלית בעלת רדיוס מציר הסימטריה.

סעיף א’

המרחק המבוקש הוא מחוץ לטורוס, כלומר . נשים לב כי:

הזרם שחוצה את מישור הלולאה הוא - הזרם דרך כל לולאה מבטל אחד את השני. לכן, מחוק אמפר:

סעיף ב’

המרחק המבוקש הוא בתוך הטורוס, כלומר . נשים לב כי:

הזרם שחוצה את מישור הלולאה הוא פשוט מספר הכריכות כפול הזרם דרך כל כריכה:

לפי חוק אמפר:

נציב נתונים:

שאלה 7

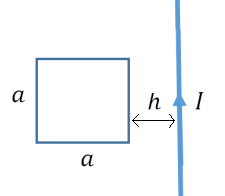
סכימת התיל והריבוע

משדה מגנטי של תיל אינסופי, אנו יודעים כי עבור מרחק מהתיל:

כאשר בכיוון מחוץ למסך. השטף דרך המסגרת הריבועית:

הנורמל לשטח הפנים של הריבוע פונה גם כן החוצה מהמסך, ולכן:

לכן:

שאלה 8

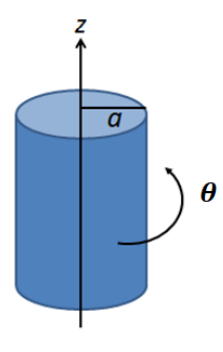
סכימת הגליל האינסופי

ניתן לחשוב על הגליל האינסופי הנתון כסליל אינסופי. מאחר ומחוץ לסליל אינסופי לא קיים שדה מגנטי, נסיק כי:

שאלה 9

סכימת הגליל האינסופי

נחשב באותו אופן כמו כוח מגנטי של גליל אינסופי, רק הפעם נשים לב כי . נבנה את אותה הלולאת אמפר:

בחירת לולאת אמפר שחלקית נמצאת בתוך הגליל

ונקבל גם כי:

נותר לחשב את . מהנתון על צפיפות הזרם:

לפי חוק אמפר:

לפי כלל יד ימין, מכוון בכיוון החיובי של :

שאלה 10

השאלה שקולה למקרה של שדה מגנטי בתוך סליל:

כאשר נשים לב כי :

נציב נתונים ונקבל: