MDN1_004 מחברים מרותכים

מבוא

נועם התחיל בלדבר במשך שעתיים על ריתוחים, ריתוכים מתחת לים, ג’עג’וע תרכובות כימיות על פסי רכבת, ריתוך עץ (???), טיג, מיג, איק, מיק, פיק וכו’.
בגדול, ריתוכים זה אחלה במצבים מסוימים, יכול להיות יותר זול מברגים, יותר אסתטי, והטרנד לאחרונה הוא פחות שימוש במסמרות ויותר ריתוכים וברגים. ניתן לקרוא עוד בתהליכי ייצור.

סימני ריתוך

הריתוכים צריכים להיות מפורטים במדויק על סכימת העבודה של חלק, וזאת נעשה בעזרת סימוני ריתוך סטנדרטיים. באיור הבא, לפי AWS - American Welding Society, מוצג סימון כזה.

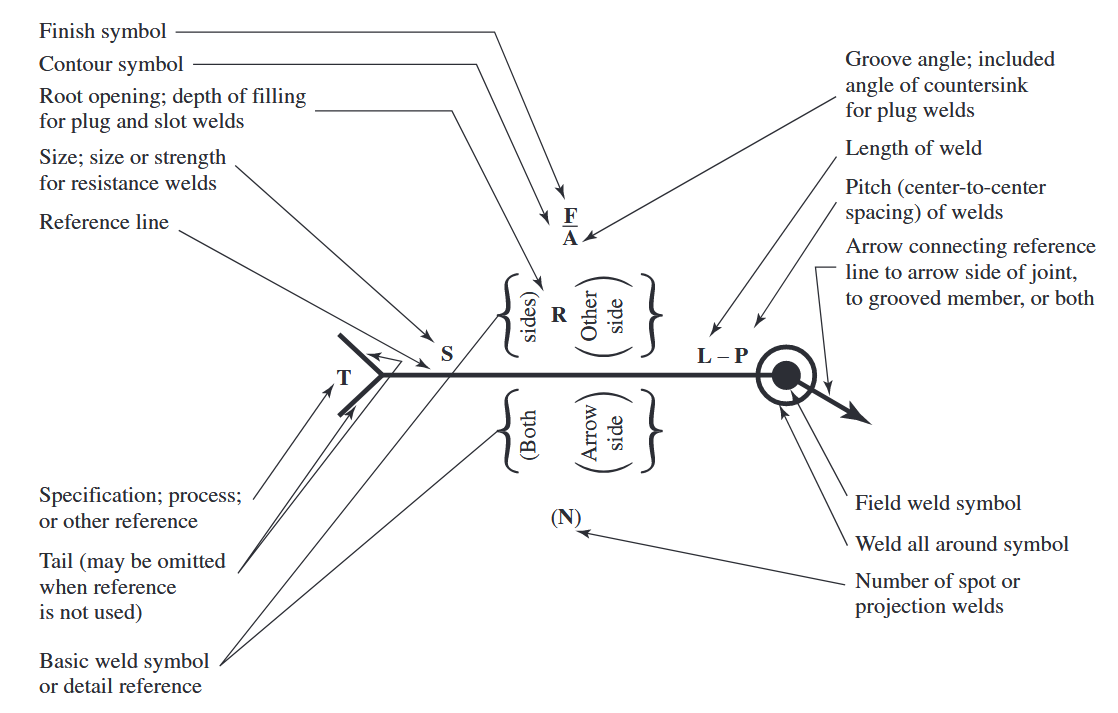
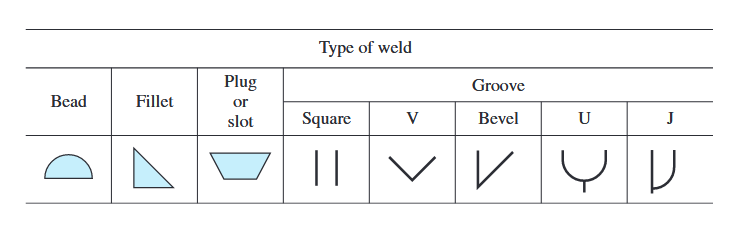
סטנדרט AWS לסימון ריתוחים. (Budynas et al., 2015).

החץ בסימון מצביע על המחבר שרוצים לרתך.

ריתוך פילט והשקה

באיור הבא מוצג מגרעת-V המועמסת באופן נורמלי ובאופן גזירה בנפרד.

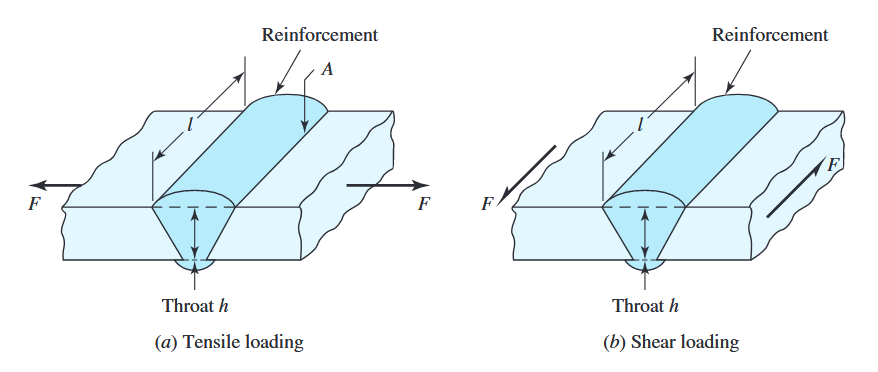
מחבר השקה טיפוסי. (Budynas et al., 2015).

עבור כל אחד מהמצבים, במידה וגודל הכוח הוא , המאמץ הממוצע המתפתח ב”צוואר” הוא:

בתאכלס, פילוג המאמצים מאוד מסובך:

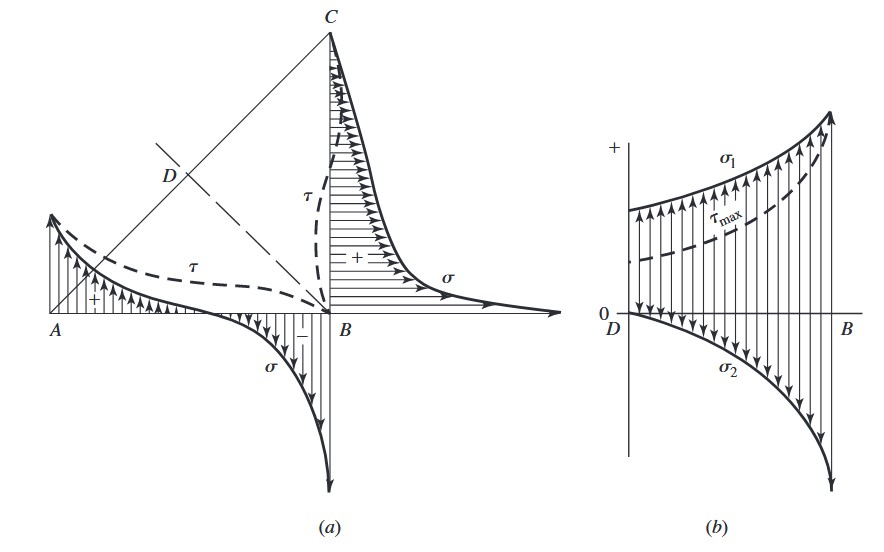
פילוג מאמצים בריתוכי פילט: (a) פילוג מאמצים על הרגליים לפי Norris; ו-(b), פילוג מאמצים ראשיים ומאמצי גזירה מקסימליים לפי Salakian. (Budynas et al., 2015).

אנו לרוב נבצע קירוב די שמרני למאמץ בתפר הריתוך. הקירוב המקובל מבוסס על:

• חישוב כשל על סמך מאמץ גזירה.
• חישוב שטח החתך הצר ביותר (נסמנו ).
• הפעלת עוצמת כל כוח על שטח החתך הצר .

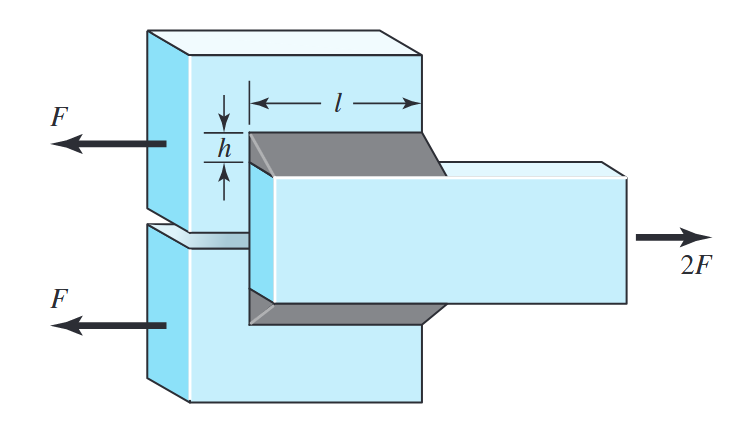
ריתוחי פילט מקבילים. (Budynas et al., 2015).

מכך אנו מגיעים למאמץ הגזירה השקול:

מבחינת מקדם ביטחון, לפי קריטריון פון מיזס:

בטבלה 9-3 מפורטים מאפיינים מינימליים לאלקטרודות שונות. יש לבחור אלקטרודה בעלת חוזק דומה לחוזק המצעים.

בטבלה 9-4 מוצגים ערכי מקדם ביטחון מותרים עבור סוגי ריתוכים שונים ועומסים שונים. אנחנו בקורס עובדים עם מקדם ביטחון עבור shear בטבלה. כלומר, אם יצא לנו למשל מקדם ביטחון , מבחינתנו החומר ייכשל.

מאמצים בריתוך

האיור הבא מתאר שלוחה (cantilever) המרותכת לעמוד ע”י שני ריתוכי פילט, כל אחד מהם באורך .

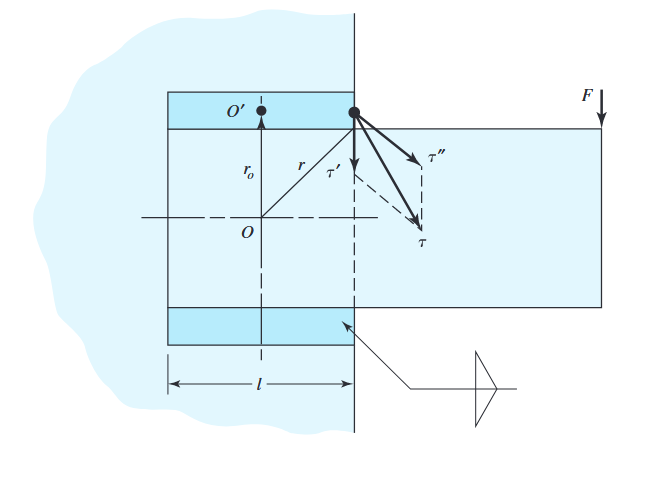
שלוחה הנתונה תחת עומס. (Budynas et al., 2015).

התגובה בריתום תמיד כולל כוח גזירה , מומנט פיתול , ומומנטי כפיפה שנניח והם בכיוונים . הכוח גזירה יותר מאמץ גזירה טהור בגודל

הפיתול יוצר

והמומנטי כפיפה יוצרים (בהנחה והנורמל למישור הריתוך הוא ):

בטבלאות 9-1 ו- 9-2, מוצגים המומנטי אינרציה הרלוונטיים. אנו נמיר את ל- ו- ע”י:

כך שכאשר נציב אותם ב- הרלוונטי, הוא כבר יהיה בתצורת המאמץ גזירה השקול , לפי משוואה .

כשל בהתעייפות

כדי לבדוק האם הריתוך עומד בעומסי התעייפות, נחשב את ו- כאשר נכלול בהם את מקדמי הריכוז מאמצים, , כנדרש. את מקדם ריכוז המאמצים לריתוך ניקח מטבלה 9-5, עבור T-butt.
כאשר נחשב את , נבחר ב- As-forged מטבלה 6-2 כאשר נחשב את . מאחר ואנו גם בפיתול (לרוב זוהי ההעמסה הנפוצה על ריתוך בהתעייפות), נבחר מקדם תיקון להעמסה, .

אם אנו רוצים למצוא את אורך החיים, נבחר במקום זאת , כי ההתחשבות בפיתול (בגזירה) נכנסת בחישוב המאמצים השקולים, לפי פון-מיזס:

נחשב את לפי קריטריון גודמן:

וכעת נוכל לחשב את לפי משוואה .

תרגילים

תרגיל 1

בציור מתואר גליל שאורכו , קוטרו החיצוני ועובי הדופן . אל הגליל מרותכים קורה בעלת חתך מלבני מלא במידות כמתואר בציור.

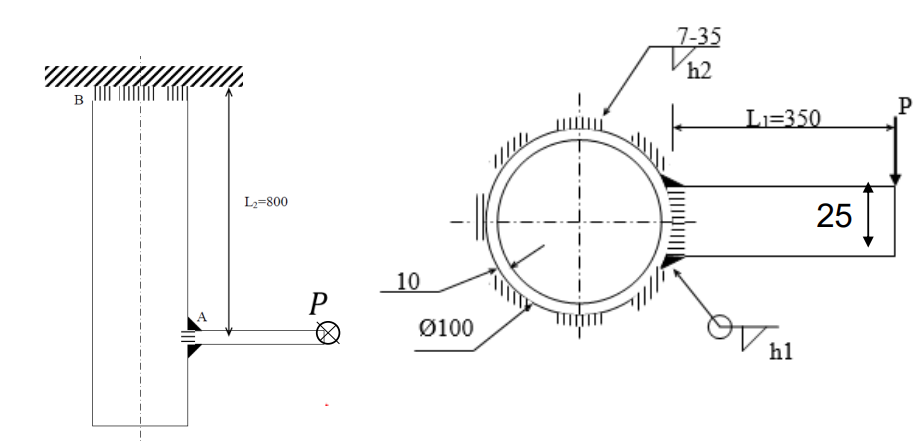
סכמת הבעיה. הקורה בעלת חתך מלבני.

כל החלקים עשויים A1 6061-T6 ומרותכים ע”י אלקטרודה מתאימה. הקורה מועמסת במשקל . עבור מקדם ביטחון .
נתוני חומר הריתוך: .

סעיף א’

חשבו את מידות הריתוך בחתך .

פתרון:
על מנת לפשט את הבעיה נניח שהריתוך הוא ישר ולא מעגלי. המחבר מועמס בכפיפה וגזירה. נחשב את מרכז הכובד ומומנטי אינרציה של צוואר הריתוך, לפי טבלה 9-2, מקרה 6:

לכן:

נחשב את המאמצים:
המאמץ עקב כוח הגזירה:

המאמץ עקב כפיפה:

נסיק שמאמץ הגזירה השקול הוא:

לכן, כדי לקיים , עובי הריתוך הדרוש הוא:

לכן נבחר ריתוך .

סעיף ב’

חשבו את מידות הריתוך בחתך .

פתרון:
חתך מועמס ע”י כפיפה, גזירה ופיתול. מהשרטוט, הריתוך מבוצע בקטעים של כל . מטבלה 9-1 מקרה 6 וטבלה 9-2 מקרה 9:

היחס בין החלקים המרותכים והלא מרותכים:

נתקן את השטח ומומנטי האינרציה:

נחשב מאמצי גזירה:

נביט בחתך כדי להבין איפה הנקודה המסוכנת ביותר:

מאמצים בחתך.

נשים לב שקיימות שתי נקודות מסוכנות אפשריות. נחשב את המאמצים בכל נקודה כדי להחליט מי יותר מסוכנת:

• נקודה בה הכפיפה מקסימלית (נקודה ):
• נקודה בה הגזירה מקסימלית (נקודה ):

נסיק שנקודה יותר מסוכנת. נמצא את עובי הריתוך שיתאים למקדם ביטחון הרצוי:

לכן נבחר ריתוך .