פנגייה

MDN1_001 מבוא לתכן מכני

מבוא

תיכון (design) הוא בניית תכנית לסיפוק צורך מסוים או לפתירת בעיה מסוימת. אם התכנית מביאה ליצירת משהו בעל מציאות פיזית, אז המוצר חייב להיות פונקציונלי (חייב לעבוד), בטוח, אמין, ניתן לייצור, ניתן לשיווק, וניתן לשימוש.
תכן מכני (Mechanical Engineering Design) כולל את כל הדיסציפלינות של הנדסת מכונות - מכניקת מוצקים וזורמים, מעברי חום ומסה, תהליכי ייצור, הנדסת מערכות ובקרה וכו’.

מאמצים, תיאוריות כשל וריכוז מאמצים

כלל החלק הראשון של הספר (Budynas et al., 2015) עובר על הקונספטים הבאים שהכרחיים להבנת המשך הקורס:

טיפ:

העוצמה של מאמץ הגזירה בחתך עקב כפיפה, כפי שראינו, הינו זניח יחסית לעומת מאמצי הכפיפה בחתך. במבחן, לרוב נזניח את מאמץ הגזירה - במידה ועושים זאת, יש לציין זאת ולנמק!

ישנם סימונים קריטיים לקריטריוני כשל בקורס:

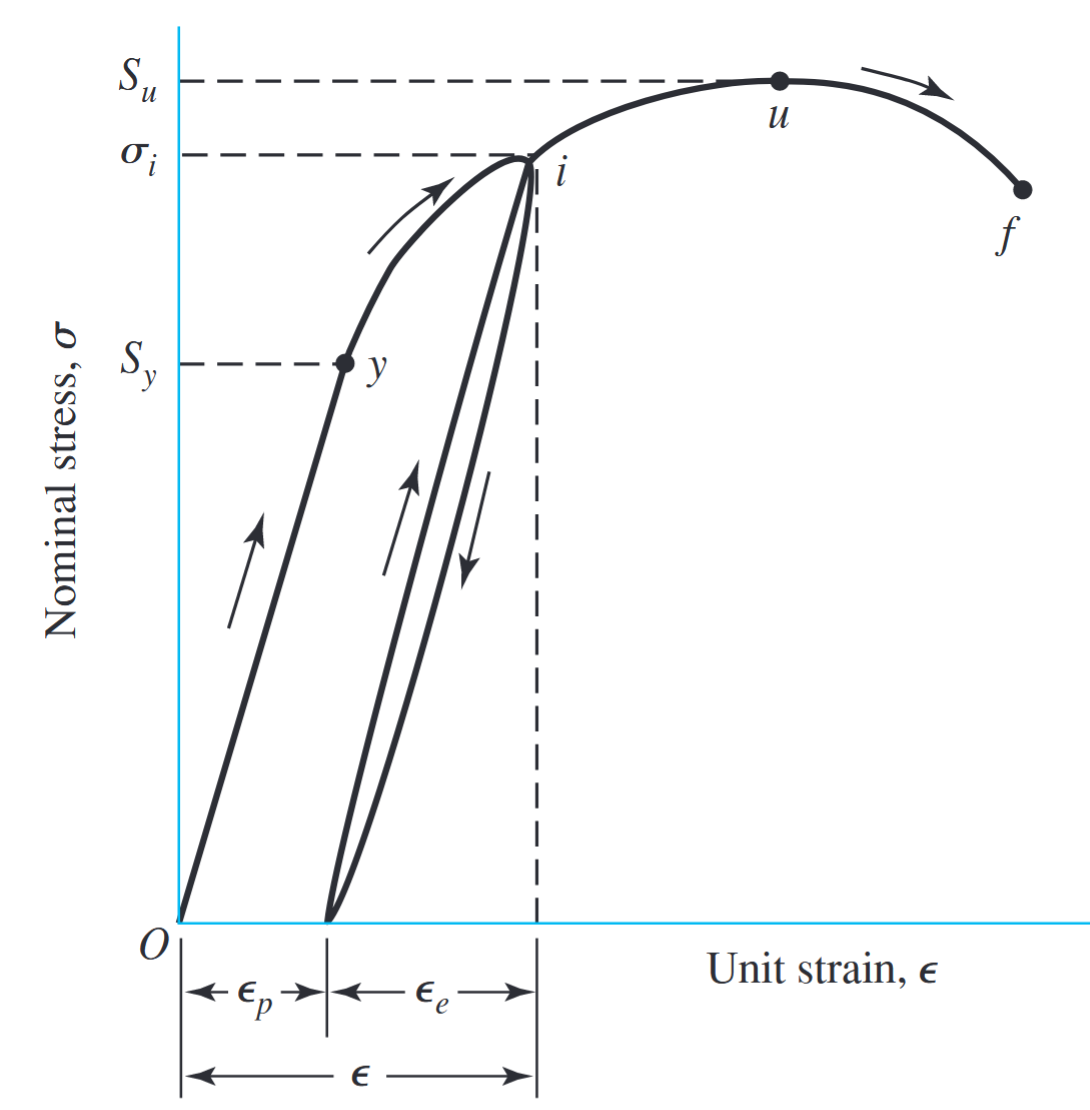
bookhue

דיאגרמת מאמץ-עיבור קלאסית, עם סימוני הקורס. (Budynas et al., 2015).

את מאמץ/חוזק הכניעה נסמן ב-, בעוד את נקודת ה-UTS נסמן ב-. את נקודת הכשל אנו מסמנים ב-.
בנוסף, כאשר אנו דנים בקריטריוני כשל, למשל עבור קריטריון טרסקה, אנו יודעים שמאמץ הכניעה בגזירה טהורה () הוא למעשה מחצית מאמץ הכניעה:

כאשר הכוונה ב- הנוסף הוא לגזירה - shear. לעומת זאת, לפי קריטריון פון מיזס, נקבל כי:

מומלץ לקרוא ב(Budynas et al., 2015) פרקים 5-4, 5-5 על פיתוח גדלים אלו.

נעבור בקצרה גם על ריכוז מאמצים, ועל תאוריית כשל קולון-מור:

ריכוז מאמצים

בפיתוח משוואות המאמצים למתיחה, לחיצה, כפיפה או פיתול, הנחנו שהגאומטריה של הגוף אחידה. אבל זה לא פשוט לעצב מכונה בלי לאפשר שינויים מסוימים בשטח חתך של הגופים השונים בו. לבורג יש ראש בצד אחד והברגה בצד שני, מה שנחשב שינוי פתאומי בשטח חתך. חלקים שונים כוללים חורים, בליטות וחריצים בצורות שונות. כל אי-רציפות בחלק מכני משנה את פילוג המאמצים בסביבת האי-רציפות, כך שמשוואות המאמצים הבסיסיות כבר לא מתארים את מצב המאמצים בחלק. אי-רציפויות אלו נקראים מגברי מאמצים, והאזורים בהם הם מתרחשים נקראים אזורי ריכוז מאמצים.

מקדם ריכוז מאמצים תאורטי או גאומטרי או הוא היחס בין המאמץ המקסימלי האמיתי באי-רציפות למאמץ הנומינלי:

כאשר הוא עבור מאמצים נורמליים ו- הוא עבור מאמצי גזירה. המאמץ הנומינלי או הוא המאמץ המחושב ע”י שימוש במשוואות המאמצים הבסיסיות וסך שטח החתך.
מקדם ריכוז המאמצים תלוי רק בגאומטריה של החלק. כלומר, לחומר בשימוש אין השפעה על הערך של . זה למה הוא נקרא מקדם ריכוז מאמצים תאורטי.
הניתוח של גאומטריות שונות למציאת מקדמי ריכוז מאמצים היא בעיה קשה, ולרוב לא ניתן למצוא פתרון אנליטי אליהן. רובם נמצאים ע”י ניסויים או ע”י שיטת אלמנטים סופיים.

הדוגמה הבאה מציגה לוח דק תחת מתיחה, עם חור עגול במרכזו:
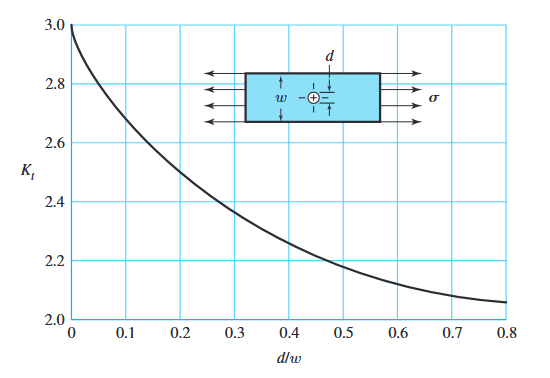
bookhue

לוח דק במתיחה עם חור עגול באמצעו. סך כוח המתיחה הוא , כאשר הוא עובי הלוח. המאמץ הנומינלי הוא:

(Budynas et al., 2015).

בעומס סטטי, אנו מתחשבים במקדמי ריכוז המאמצים באופן הבא. בחומרים משיכים (, כאשר הוא העיבור בו הדגם נכנע), אנו לא לוקחים בחשבון את מקדם ריכוז המאמצים כדי לחשב את המאמץ הקריטי לכניעה, כי העיבור הפלסטי באזור של הריכוז מאמצים הוא מקומי ואף מונע את הכשל בשל תופעת הקשיית מעוותים. בחומרים פריכים (), הריכוז מאמצים נלקח בחשבון על המאמץ הנומינלי לפני שמשווים אותו לחוזק החומר.

בעומס דינמי, השפעת ריכוז המאמצים היא משמעותית עבור גם חומרים משיכים וגם חומרים פריכים, ותמיד צריך להילקח בחשבון.

דוגמה:

לוח בעובי נתון באופן הבא:
![[2027DE8C-D757-4253-A842-FF74545915C8-removebg-preview.png|bookhue|500]]
הלוח מועמס בכוח קבוע של . הוא עשוי מחומר שעבר טיפול תרמי וחוסם בשביל לחזק אותו, אבל כתוצאה מכך איבד את רוב הגמישות שלו. רצוי לקדוח חור דרך מרכזו של הפאה באורך כדי לאפשר לכבל לעבור דרכו. חור בקוטר מספיק בשביל שהכבל יעבור, אבל ישנו גם מקדח בקוטר אם נדרש. איפה יש יותר סיכויים שסדק יופיע - בחור הגדול, הקטן, או בכלל בפילט (fillet)?

פתרון:
כיוון שהחומר פריך, השפעת ריכוז המאמצים סביב אי-הרציפויות חייבת להילקח בחשבון. במקרה של חור בקוטר המאמץ הנומינלי הוא:

מקדם ריכוז המאמצים התאורטי, מטבלת מקדמי ריכוז מאמצים, עם , הוא . לכן המאמץ המקסימלי הוא:

באותו אופן, עבור החור בקוטר , נקבל ו- , ולכן:

עבור הפילט, מתקיים:

מאותה הטבלה, נשים לב שבמקרה שלנו ו- , ולכן . נקבל ש:

הסדק כנראה יתרחש עם החור בקוטר , לאחר מכן בחור בקוטר , ולבסוף בפילט.

תאוריית קולון-מור לחומרים משיכים

לא לכל החומרים יש חוזק לחיצה השווה לחוזק המתיחה שלהם. למשל, המאמץ כניעה של סגסוגות מגנזיום בלחיצה יכול להיות מחצית מהמאמץ כניעה שלו במתיחה. החוזק של ברזל אפור יצוק בלחיצה נע בין פי 3 ל-4 יותר גדול מהחוזק שלו במתיחה. בחלק זה נדון בתאוריית קולון-מור לחומרים משיכים (DCM - Ductile Coulomb-Mohr) שיכולה לחזות כשלים עבור חומרים שחוזקם במתיחה ולחיצה לא שווים.

לא נעמיק בפיתוח של תאוריה זו, מספיק לדעת שלפיה, אם המאמצים הראשיים הם :

כאשר:

  • המאמצים ו- הם המאמצים הראשיים, הכי גדול ו- הכי קטן.
  • הביטויים ו- הם החוזק של הדגם במתיחה ולחיצה בהתאמה.
  • הביטוי הוא מקדם הביטחון.

עבור מצב מאמצים מישורי, בו המאמצים הראשיים הם ו- , התנאים לכשל הם:

  • אם , אז זה אומר ש- ו- , ואז המשוואה לעיל הופכת ל:
  • אם , אז זה אומר ש- ו- , ואז המשוואה הופכת ל:
    $$
    \dfrac{\sigma_{A}}{S_{t}}-\dfrac{\sigma_{B}}{S_{c}}\geq 1
  • אם , אז זה אומר ש- ו- , ואז המשוואה הופכת ל:
    $$
    \sigma_{B}\leq -S_{c}

נוכל לצייר גרף שמתאר את תנאים אלו:
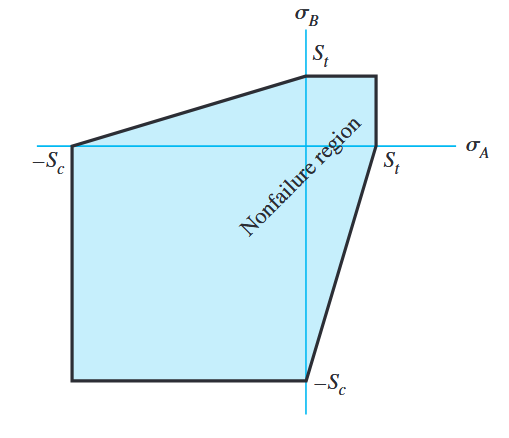
bookhue

גרף לתאוריית קולון-מור למצב מאמצים מישורי. (Budynas et al., 2015).

תיקונים לתאוריית מור עבור חומרים פריכים

עבור חומרים פריכים, קיימים שני שינויים של תאוריית מור לחומרים פריכים: תאוריית קולון-מור לחומרים פריכים (BCM - Brittle Coulomb-Mohr) ותאוריית מור המתוקנת (MM - Modified Mohr). המשוואות לתאוריות אלו יינתנו למצב מאמצים מישורי.
נסתפק בקורס זה בתיאור הגרפי שלהם:
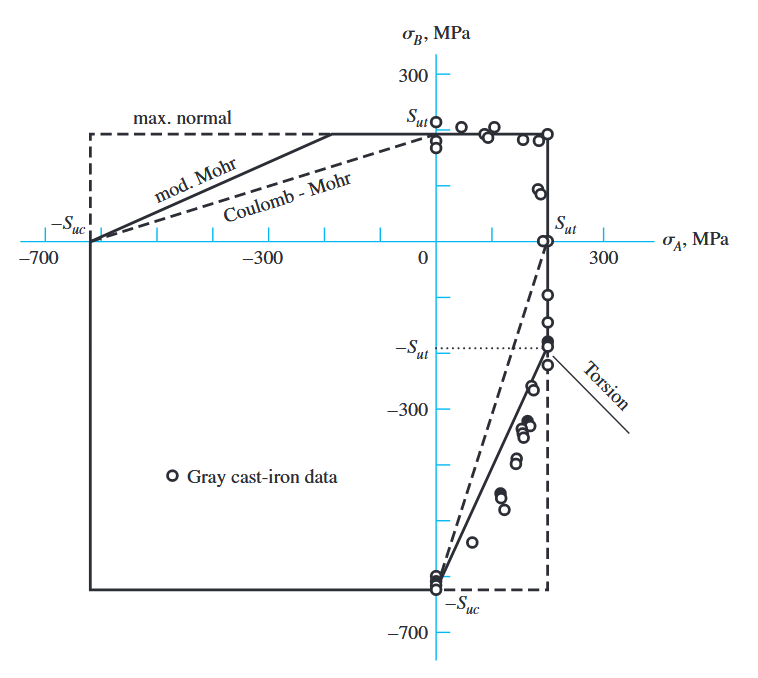
bookhue

תיאור דו-צירי של כשל של ברזל יצוק אפור בהשוואה לקריטריונים השונים לכשל. (Budynas et al., 2015).

תרגילים

תרגיל 1

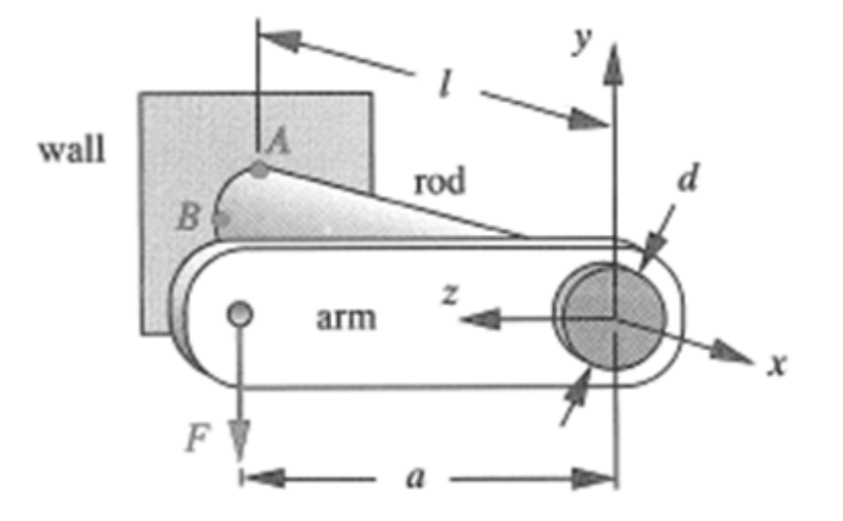
bookhue

סכמת הבעיה

הקורה שבאיור עשויה פלדה בעלת חוזק כניעה . לקורה מחוברת זרוע ובקצה מופעל כוח אנכי בשיעור .
נתונים נוספים:

בפתרון יש להניח שהזרוע קשיחה לחלוטין.

סעיף א’

שרטט מהלך כוחות ומומנטים.

פתרון:

(משמאל לימין, מלמעלה למטה) דג”ח על כלל המערכת, חתך שלילי על קורה , חתך שלילי על קורה מזווית שונה.

מהדג”חים והחתכים לעיל אנו יכולים להסיק כי:

מהלכי כוחות גזירה, מומנטי כפיפה ומומנטי פיתול

סעיף ב’

מהו החתך הקריטי ומהי הנקודה הקריטית?

פתרון:
החתך הקריטי הוא ב- - שם נמצא המומנט כפיפה הכי גדול (הפיתול והגזירה אחידים לאורך החתך).

סעיף ג’

חשב מאמצים ראשיים בנקודה הקריטית.

פתרון:
לפי מאמץ נורמלי בכפיפה אנו יודעים ש:

כאשר הכוונה ב- היא ל-bending. במקרה שלנו, או . בנוסף, עבור שטח חתך עגול מלא, מMDN1_A18 טבלת תכונות גאומטריות, . לכן המאמץ המקסימלי, שיתקבל עבור :

אנו גם יודעים שמאמץ הגזירה בפיתול הוא:

שוב, מהטבלאות אנו יודעים שעבור החתך הנתון מתקיים ולכן:

בנוסף, המאמץ גזירה עקב כפיפה, לפי טבלה 3-2:

נשים לב כמובן שכל אחד מהמאמצים שחישבנו נכונים רק עבור נקודה אחת או כמה נקודות על החתך :

המאמצים הפועלים בנקודות הקיצון השונות בחתך.

נשים לב שנקודות הן זהות, חוץ מהסימנים שלהם. לכן נסתפק בלנתח את בלבד. בנוסף, קל לראות ש- יותר מסוכנת מ-, ולכן מבין שתיהם נבדוק רק את .

מבין שתי הנקודות, נחליט מי מהן הקריטית יותר לפי קריטריוני כשל. כך או כך, שתיהן יהיו אחת מהנקודות החשודות לכשל כי כפי שהסברנו הן יותר מסוכנות מ-, וב- המאמץ הוא לחיצה, לעומת בו המאמץ הוא מתיחה, שאנו מחשיבים יותר מסוכן (רוב החומרים רגישים יותר למתיחה מאשר לחיצה).

סעיף ד’

מצא מקדם ביטחון ע”פ שלושת קריטריוני הכשל.

פתרון:

הערה:

כל אחת מהנוסחאות עבור הקריטריונים פושטה למקרה המישורי, שהוא הרלוונטי למקרה שלנו, ולכן הנוסחאות נראות יותר פשוטות ממה שאנו זוכרים ממוצקים 2. בנוסף, הנחנו שהמאמצים הראשיים הם .

נסיק כי:

  • ע”פ כל שלושת הקריטריונים נקודה יותר מסוכנת כי היא במתיחה
    (למרות שמבחינת הקריטריונים היא זהה ל-).
  • קריטריון טרסקה הוא הקריטריון המחמיר יותר.

תרגיל 2

תמך בצורת נתמך ומועמס בכוח כמוראה בציור. פלטה (בשחור) מפעילה כוח גזירה של על חתך בלבד. התמך עשוי פלדת נתך בעלת מאמץ כניעה . חשב את מקדם הביטחון של התכן לכניעה לפי כל אחד מקריטריוני הכשל בחתכים וב-.
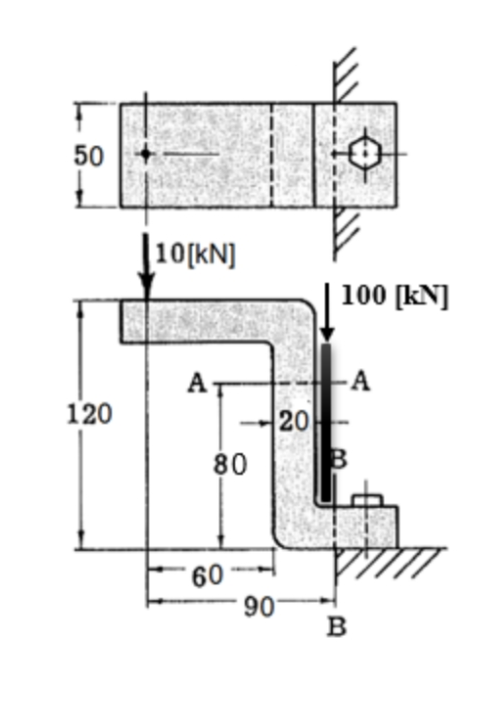
bookhue

סכמת הבעיה. המידות במ”מ.

פתרון:
נמצא את העומסים הפועלים בחתך :

שטח חתך וחתך שלילי ב-

מהדג”ח ומשיווי משקל:

לכן, לפי מאמץ נורמלי בכפיפה משופעת, בסימוני הקורס, המאמץ הנורמלי בכיוון הוא:

מMDN1_A18 טבלת תכונות גאומטריות אנו יודעים ש- , ולכן:

ניתן לראות שנקבל מאמץ מקסימלי עבור (הערך הכי קטן של ), ולכן:

נציב נתונים ונקבל:

לכן טנזור המאמץ בנקודה זו:

מאחר וטנזור המאמץ יחסית פשוט, המאמץ השקול לפי כל אחד מהקריטריונים הוא פשוט , כך שלפי כולם, מקדם הביטחון הוא:

נמצא את העומסים הפועלים בחתך :

שטח חתך וחתך חיובי ב-

מהדג”ח ושיווי משקל נמצא כי:

אבל, אנו צריכים להיכנס לרזולוציה יותר גבוה - אכפת לנו איזה כוחות גזירה. נשים לב ש- הוא כוח גזירה טהור באופן כזה שהוא לא משפיע על המאמץ גזירה עקב כפיפה, לעומת שהוא כוח גזירה היוצר כפיפה בחתך, ולכן כן נתחשב בו בנוסחה למאמץ גזירה עקב כפיפה.
המאמץ הצירי עקב כפיפה:

הביטויים הקיצוניים ל- הם ולכן:

המאמץ גזירה עקב כפיפה בציר הניטרלי (ניעזר בטבלה 3-2 לחתך מלבני):

המאמץ גזירה עקב גזירה טהורה, הפועלת בכל החתך:

לכן טנזור המאמץ ב- :

כך שהמאמצים הראשיים הם:

לפי כל אחד מהקריטריונים:

לכן מקדם הביטחון המחמיר ביותר יהיה לפי טרסקה:

ב- :

ולכן טנזור המאמצים הראשיים:

כאשר נמצא את המאמץ האקוויוולנטי לפי כל הקריטריונים, נראה כי טרסקה הכי מסוכן:

כך שהמקדם ביטחון הוא: