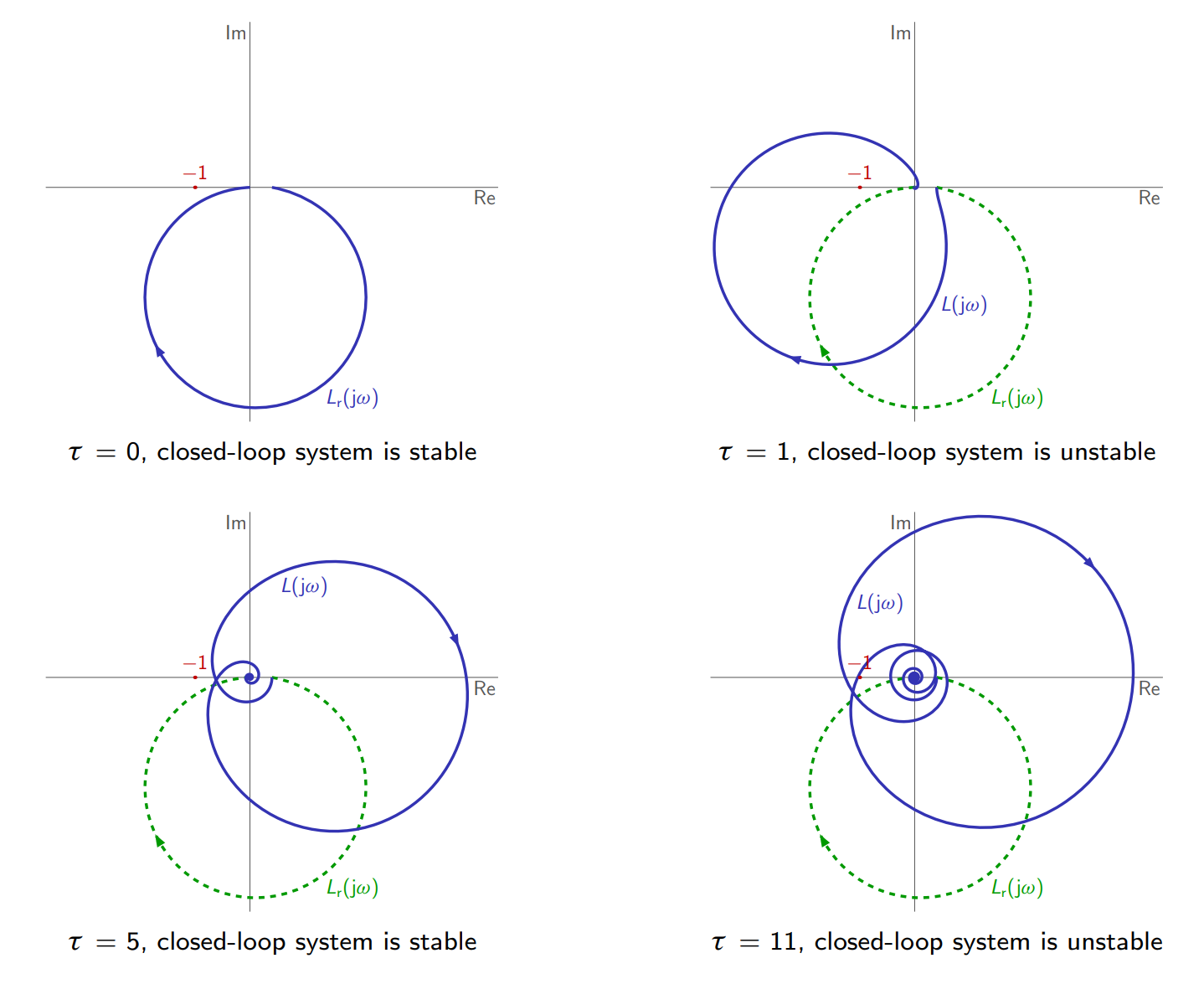
עודפי יציבות
עודפי הגבר ופאזה
בהנחה ומערכת בחוג סגור יציבה:
הגדרה: עודף הגבר ופאזה
עודף הגבר
הוא המקדם המינימלי עבורו ההגבר בחוג סגור יהפוך את החוג הסגור ללא-יציב.
עודף פאזההוא הגודל המינימלי עבורו הפאזה בחוג סגור תהפוך את החוג הסגור ללא-יציב.
בשני המקרים, התוצאה של השינוי בהגבר ובפאזה יגרום לעקום נייקוויסט לחתוך את הנקודה הקריטית.
מה קורה כאשר רק ההגבר משתנה?
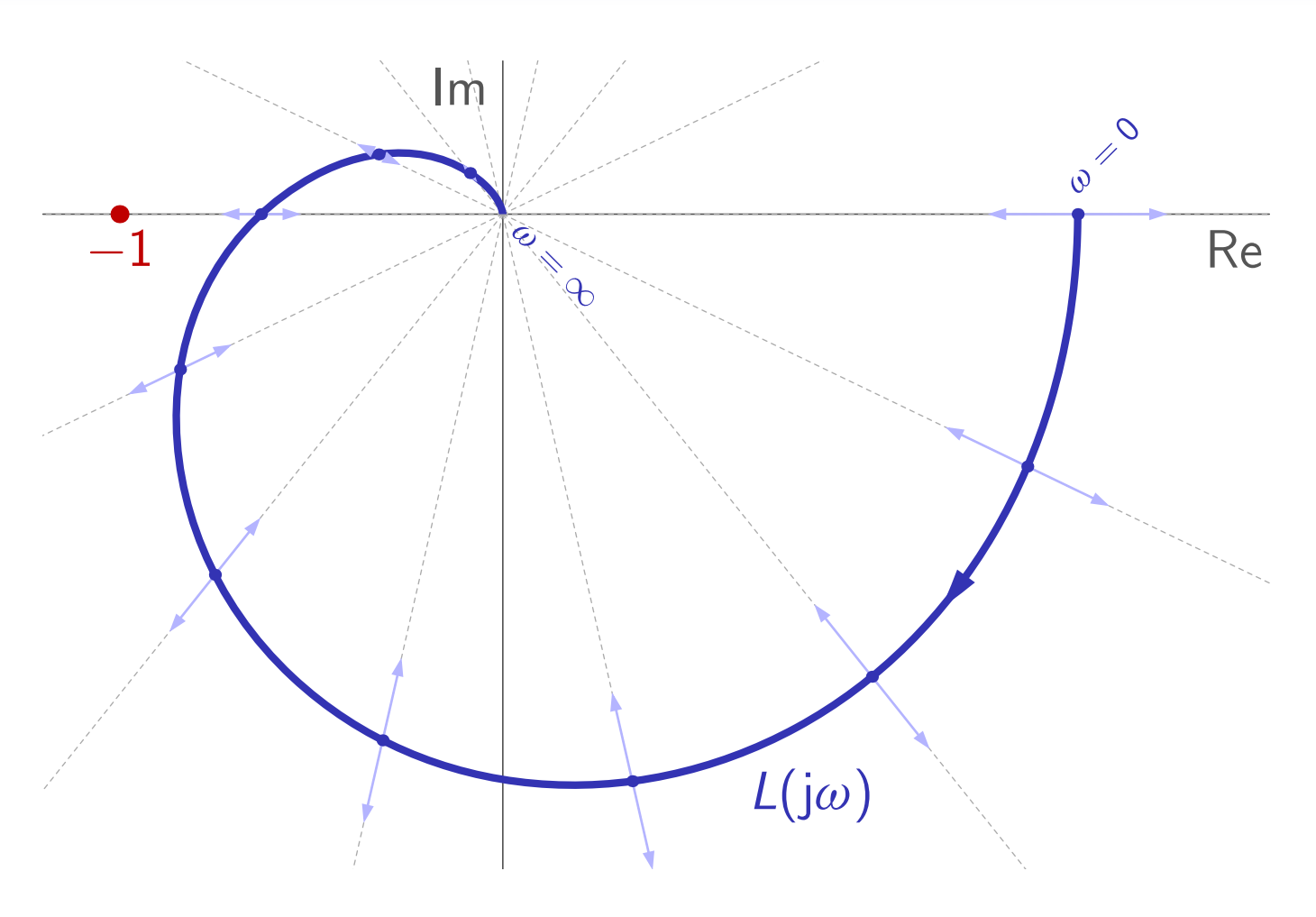
כאשר ההגבר בחוג גדל, העקום הפולארי מתנפח. כאשר ההגבר בחוג קטן, העקום הפולארי מתכווץ.
מבחינת
לתדרים בהם המעבר מתרחש קוראים תדרי מעברי פאזה
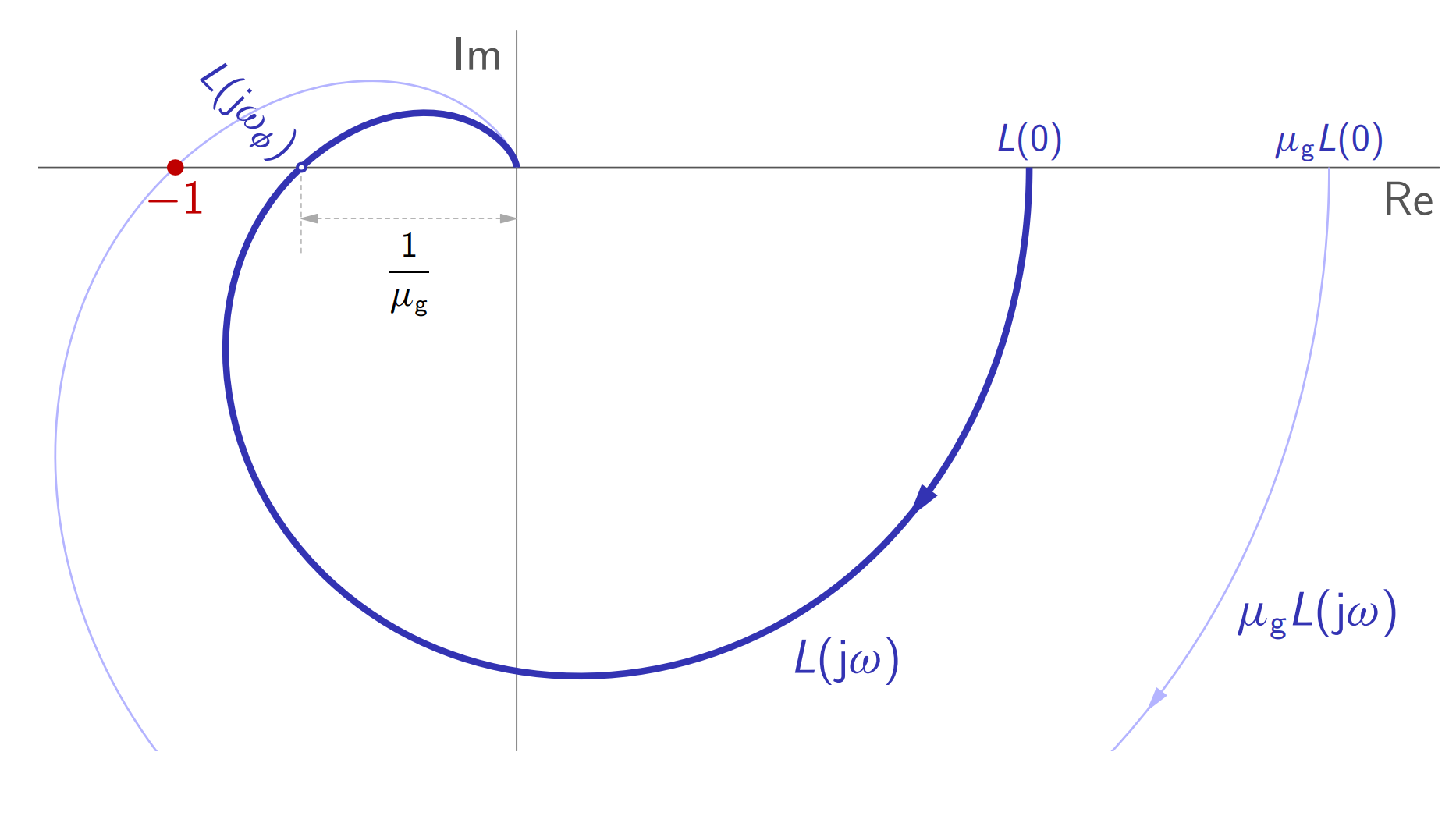
התנפחות עקום נייקוויסט עד לחיתוך עם הנקודה הקריטית.
מה קורה כאשר רק הפאזה משתנה?
כאשר הפאזה גדלה, נקודות על הגרף הפולארי מסתובבות נגד כיוון השעון. כאשר הפאזה קטנה, נקודות על הגרף הפולארי מסתובבות עם כיוון השעון.
מבחינת
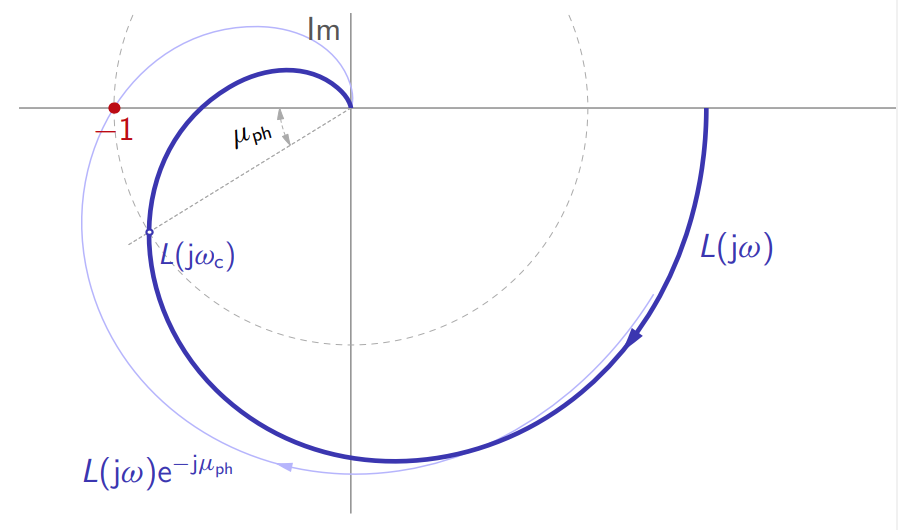
סיבוב עקום נייקוויסט עד לחיתוך עם הנקודה הקריטית.
נזכור שלתדירות בחיתוך עם נקודה זו אנו קוראים תדירות מעבר.
עודפי הגבר ופאזה בדיאגרמת בודה
כדי לחשב את
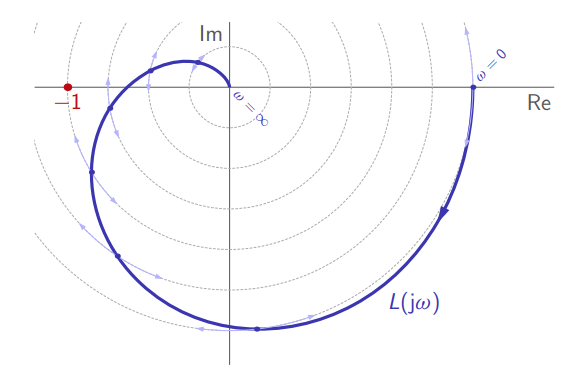
- עודף ההגבר
מחושב מדיאגרמת ההגבר ב- . אם המערכת בחוג סגור יציבה, אז שווה לערך המוחלט של ההגבר של ב- . - עודף הפאזה
מחושב מדיאגרמת הפאזה ב- . אם המערכת בחוג סגור יציבה, אז שווה למרחק בין ולנקודה הכי קרובה .
למשל, עבור
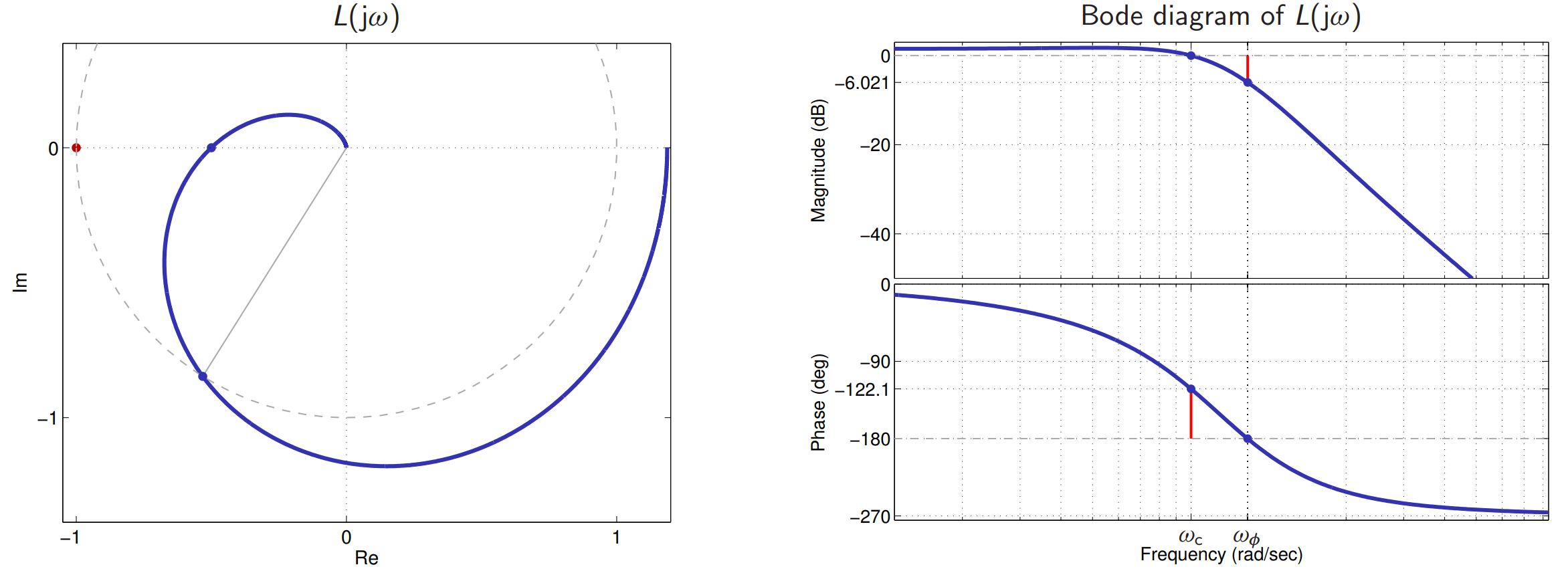
מציאת עודף הגבר ועודף פאזה בדיאגרמות בודה ונייקוויסט.
נסכם:
הוא המרחק מהנקודה הקריטית לאורך הציר הממשי. הוא המרחק (הזוויתי) מהנקודה הקריטית.
לפיכך, כאשר אנו דורשים שעקום נייקוויסט יהיה “רחוק מהנקודה הקריטית”, אנו למעשה מקיימים את הדרישה שעודפי היציבות יהיו יחסית גדולים.
כלל אצבע כללי הוא לשמור על עודפי הגבר ופאזה בסדרי גודל:
השהייה
נזכור ממערכות לינאריות שמערכת השהייה היא מהצורה:
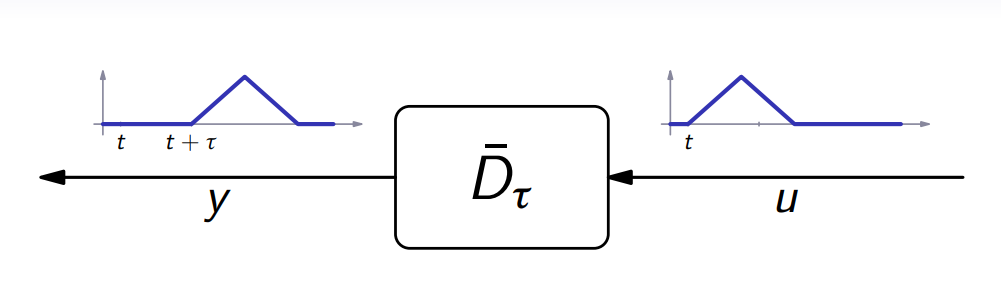
הקשר המתמטי:
מערכת זו:
- לינארית, כי:
- לא קבועה בזמן, כי:
- יציבה BIBO, כי:
לפי התמרת לפלס, פונקציית התמסורת של ההשהיה היא:
פונקציית תמסורת זו אי-רציונלית, ולכן אנו אומרים ש-
מבחינת גרף בודה, היא תיראה מהצורה:
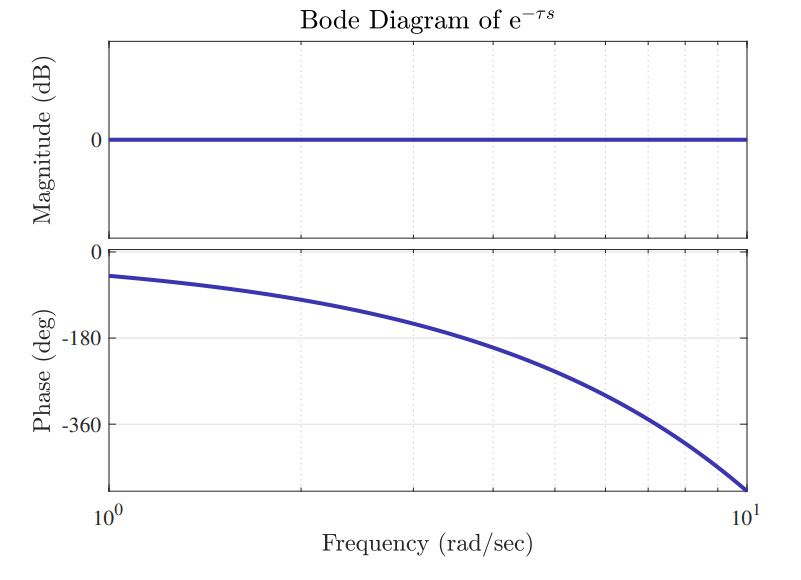
גרף בודה של
.
נשים לב של-
מערכות בזמן מת
להלן מערכת בחוג סגור עם השהייה:
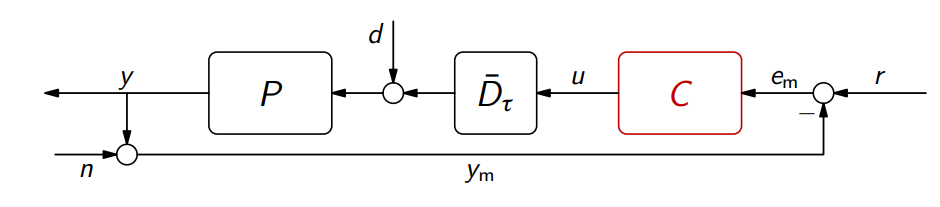
למערכות כאלו אנו קוראים מערכות בזמן מת.
בהנחה ו-
לפולינום אופייני זה יש אינסוף שורשים (נקרא גם קוואזי-פולינומי).
דוגמה:
אם
ו- , אז: לפולינום זה יש שורשים ב:
לכל
.
נשווה בין המקרה ללא השהייה והמקרה עם השהייה. בכללי, נקבל אין סוף שורשים:
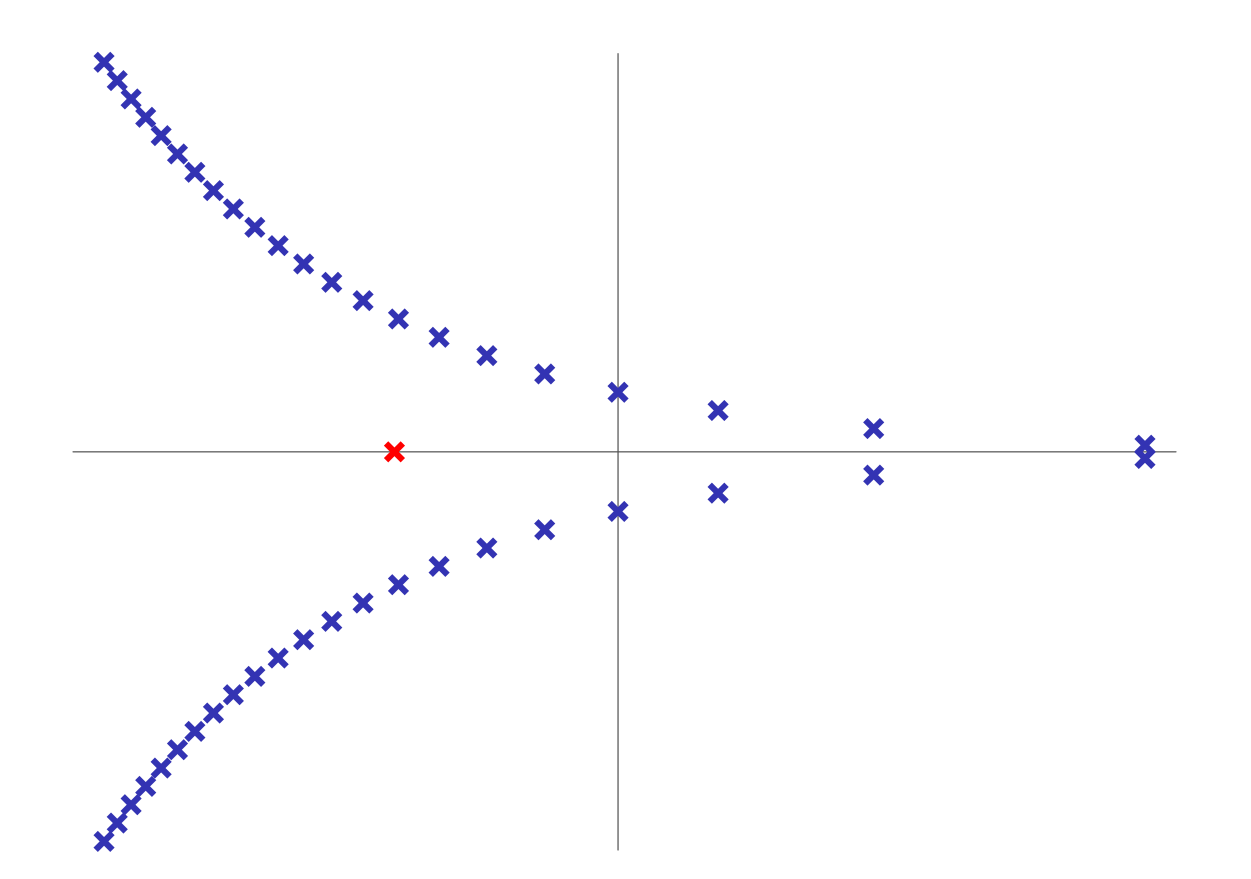
מיקומי שורשים של פולינום עם השהייה (
) ובלי השהייה ( ).
ניתן לראות מהגרף שההוספה של השהייה מסבכת משמעותית את ניתוח היציבות של המערכת.
השפעת השהייה על פונקציית החוג הפתוח
יהי
במקרה זה:
לכן:
במילים אחרות, השהיה במקרה זה:
- לא משנה את ההגבר של
. - מוסיפה פיגור בפאזה הפרופורציונית ל-
.
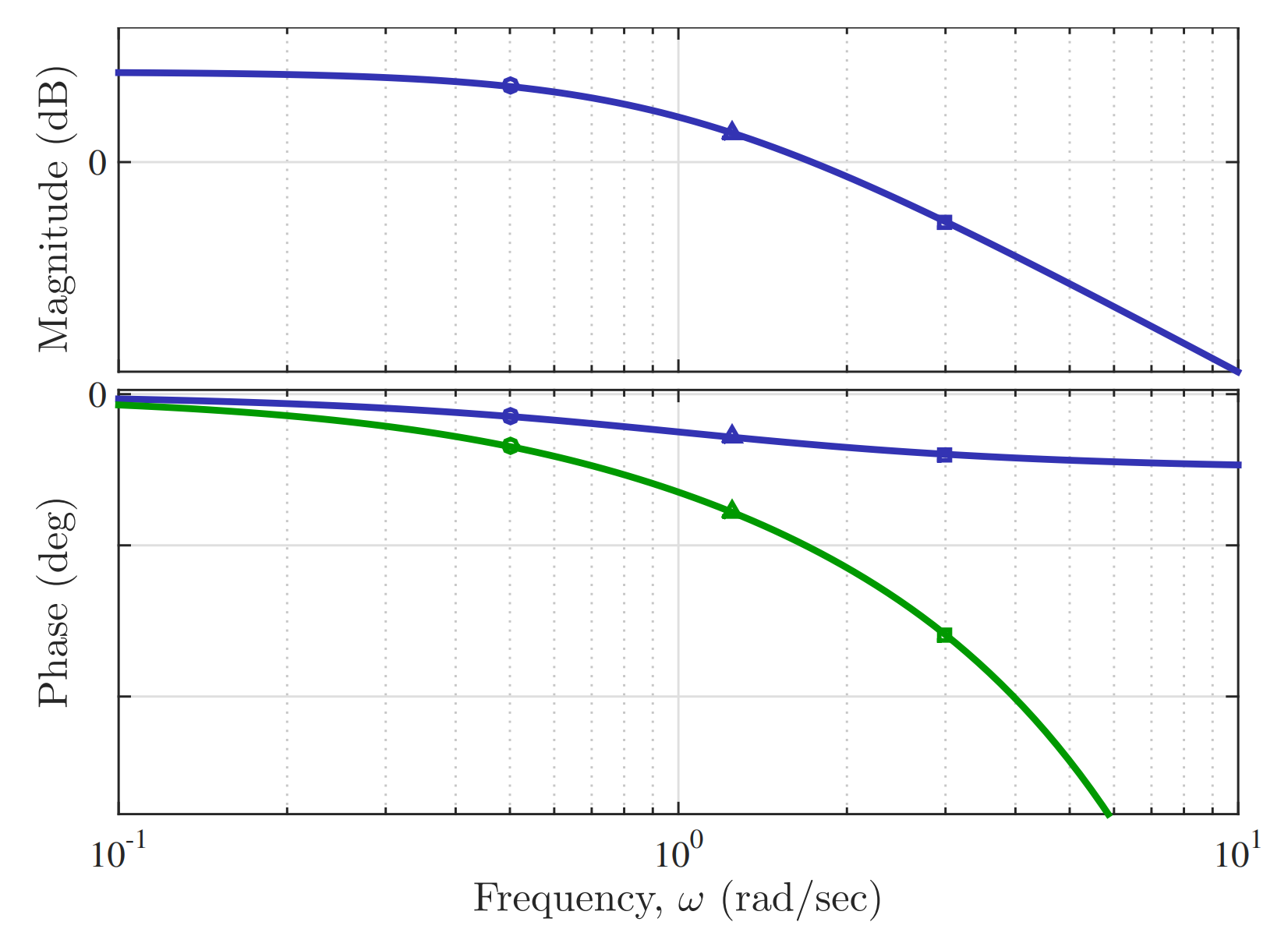
השפעת השהייה על דיאגרמת בודה של פונקציית החוג הפתוח.
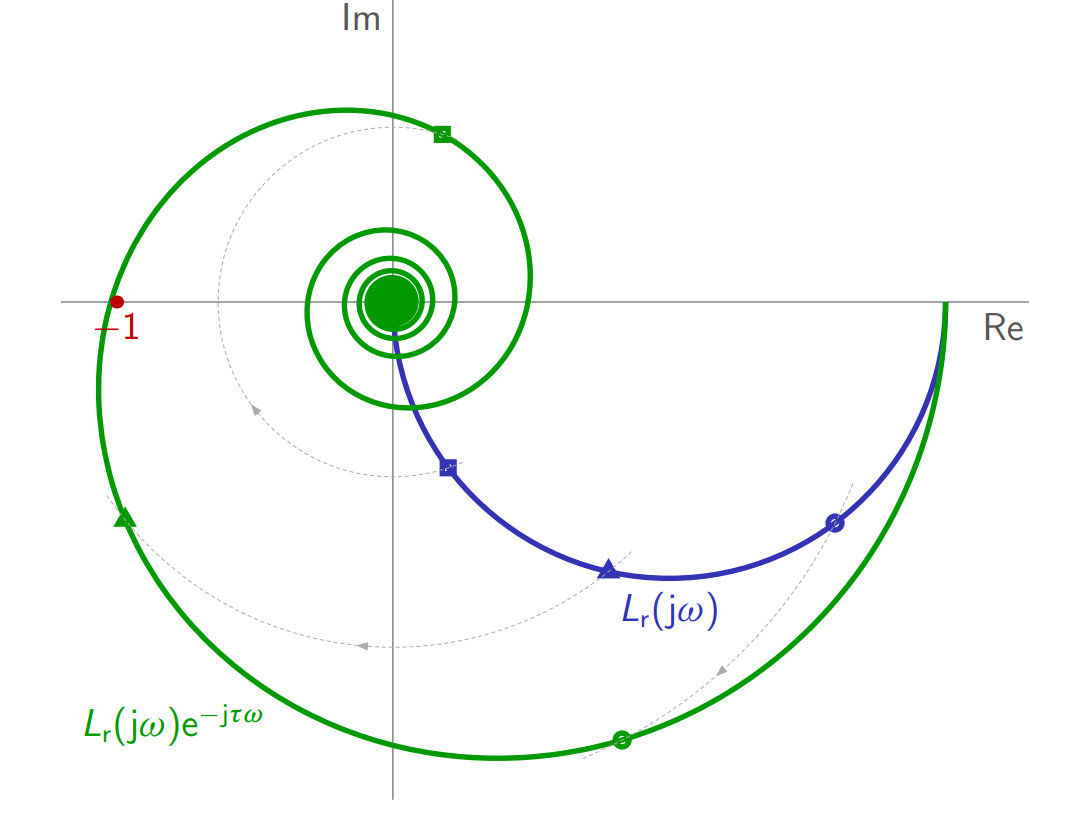
השפעת השהייה על דיאגרמה פולארית של פונקציית החוג הפתוח.
קריטריון נייקוויסט למערכות בזמן מת
ההוספה של השהיה לא משנה משמעותית את קריטריון נייקוויסט עצמו, אלא רק את הגרף הפולארי של המערכת אותה אנו חוקרים. אנו יכולים לומר זאת כי:
- גם
וגם עדיין מרומורפיים (גזירים למקוטעין רק במובן של פונקציות מרוכבות), אז עיקרון קושי עדיין תופס. - אם
, אז ל- יש מספר סופי של קטבים ב- , כך שכולם נמצאים בקונטור נייקווסיט.
דוגמה:
יהי
. אז:
עודף זמן מת
ראינו שבגלל צורה ההשפעה של השהיה על מערכת, נוכל להיעזר ה-
כך ש:
כלומר, לשתי פונקציות התמסורת אותו עודף פאזה
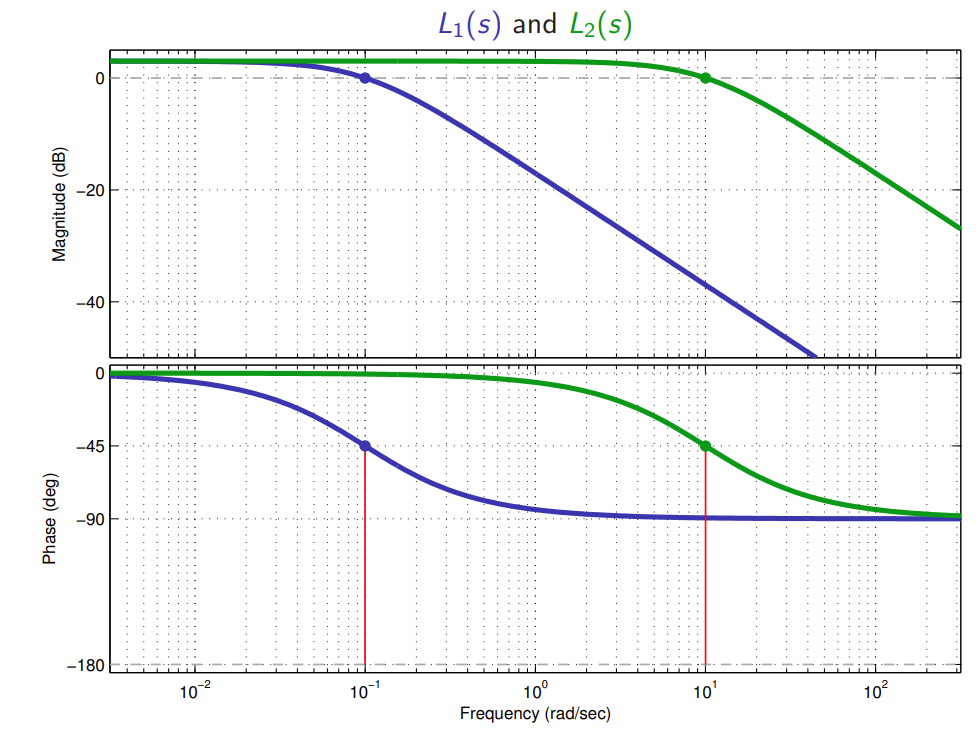
דיאגרמת בודה של
ו- .
הגרפים הפולאריים של שתי פונקציות אלו מתלכדים:
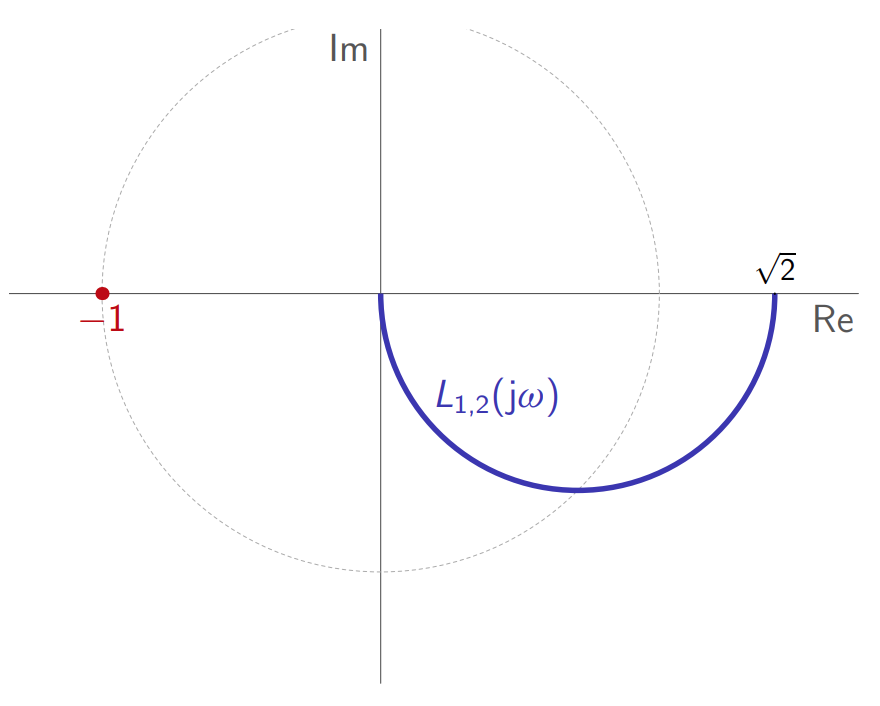
גרפים פולאריים של
ו- .
אבל, כאשר נוסיף השהייה ב-
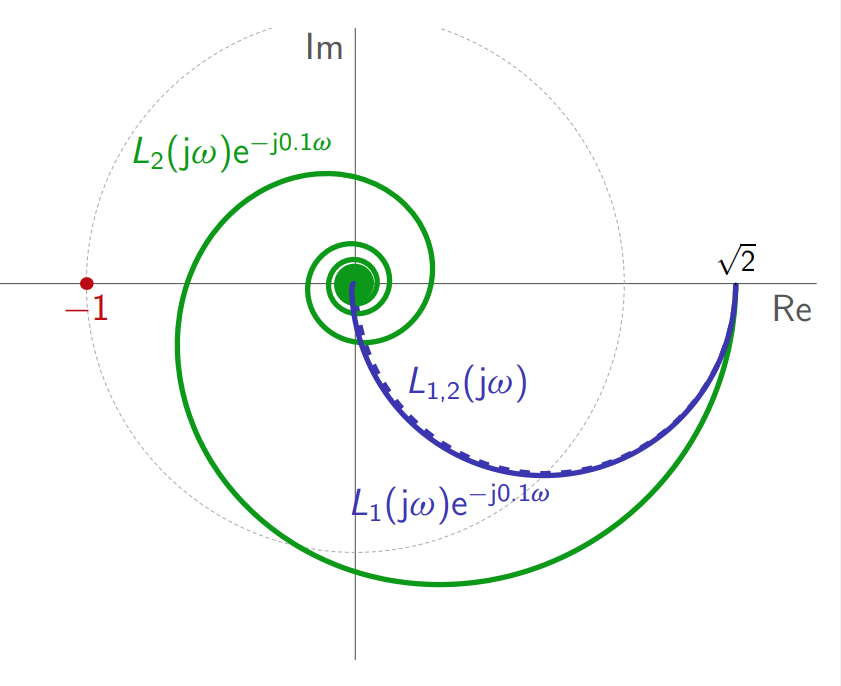
גרפים פולאריים של
ו- .
לכן, ל-
עודף זמן מת
הגדרה: עודף זמן מת
עודף זמן מת
הוא ההשהיה המינימלית שתגרום לחוג הסגור להפוך להיות לא יציב.
חישוב עודף זמן מת:
נניח כי:
- המערכת בחוג סגור יציבה.
- ל-
יש רק תדירות מעבר אחת. - מתקיים
.
אם השהיה, נגיד
המערכת נהיית לא יציבה עבור
כאשר
שוויון זה מעיד על כך שככל שתדירות המעבר