HTF1_001 מבוא

מה ואיך

מתרמודינמיקה אנו יודעים שאנרגיה יכולה לעבור ע”י אינטראקציות בין המערכת וסביבתה. לאינטראקציות אלו קוראים עבודה וחום. לעומת תרמודינמיקה, העוסקת במצבי קיצון (תחילת וסוף התהליך), בקורס זה נעסוק במהלך האינטראקציות, בפרט במנגנוני המעברי חום וקצבי מעברי חום.

הגדרה: מעבר חום

מעבר חום או הוא אנרגיה תרמית בתנועה כתוצאה מהפרש טמפרטורות.

כאשר יש הפרש טמפרטורות בין גופים/מערכות, מעבר חום חייב להתרחש.
כפי שניתן לראות באיור הבא, אנו מתייחסים לשלושה סוגים של תהליכי מעברי חום כמנגנונים:

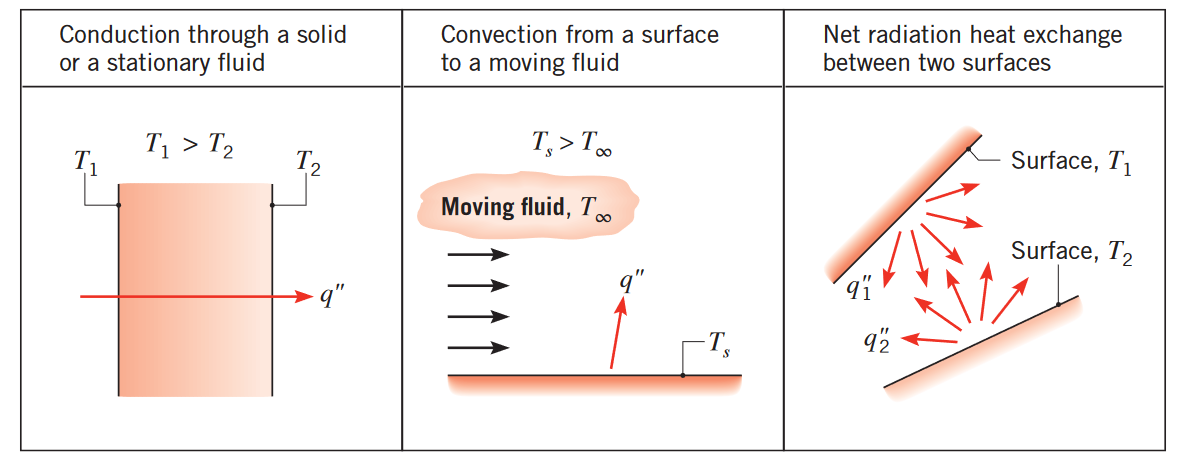
מגנוני הולכה, הסעה וקרינה. (Bergman & Lavine, 2017).

כאשר קיים גרדיאנט טמפרטורה בתווך קבוע, שעשוי להיות מוצק או זורם, אנו משתמשים במונח הולכה כדי להתייחס למעבר חום שמתרחש לאורך התווך.
מנגד, המונח הסעה מתייחס למעבר חום שמתרחש בין משטח וזורם כאשר הם נמצאים בטמפרטורות שונות. המנגנון השלישי של מעבר חום נקרא קרינה תרמית. כלל המשטחים בעלי טמפרטורה פולטים אנרגיה ע”י גלים אלקטרומגנטיים. לכן, בהיעדר תווך, ישנו מעבר חום ע”י קרינה בין שני משטחים בטמפרטורות שונות.

מקורות פיזיקליים ומשוואות הקצב

הולכה

ניתן לחשוב על הולכה כמעבר אנרגיה מהחלקיקים היותר אנרגטיים לפחות אנרגטיים כתוצאה מאינטראקציות בין החלקיקים.
כדי להסביר את המכניזם הפיזיקלי העומד מאחורי הולכה, נביט בגז חופשי:

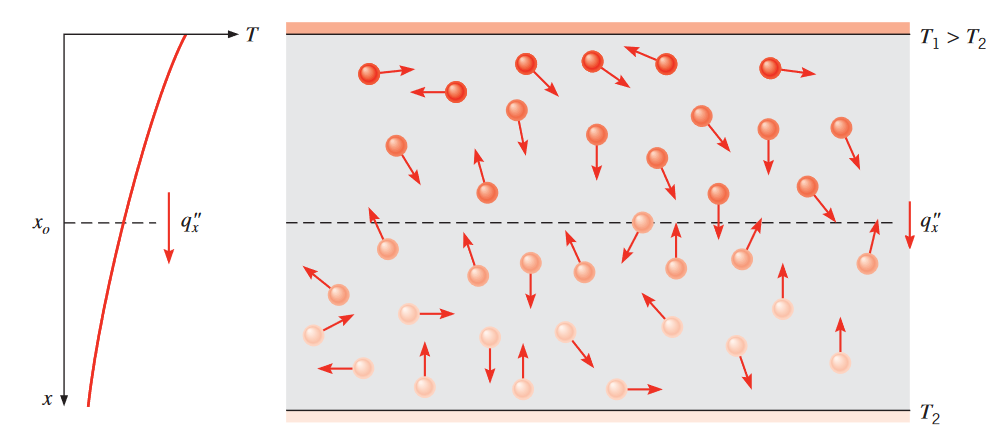
הקשר בין הולכה לדיפוזיה של אנרגיה כתוצאה מפעילות מולקולרית. (Bergman & Lavine, 2017).

נניח שבגז קיים גרדיאנט טמפרטורות, ונניח שאין תנועה מקרוסקופית (כאשר נעשה zoom-out, לא קיימת תנועה משמעותית של הגז). נוכל לקשר בין הטמפרטורה בכל נקודה עם האנרגיה של המולקולות הקרובים לנקודה. האנרגיה הזאת קשורה לתנועה הרנדומלית של החלקיקים, סיבובם סביב עצמם, והרטט שלהם.
טמפרטורות יותר גבוהות מעידות על אנרגיות מולקולרית גבוהות יותר. כאשר מולקולות שכנות מתנגשות, מתרחש מעבר של אנרגיה מהמולקולה האנרגטית יותר למולקולה הפחות אנרגטית. דרך המישור השרירותי ב- המופיע באיור כל הזמן עוברים מולקולות מעליו ומתחתיו כתוצאה מהתנועה הרנדומלית שלהן. אבל, המולקולות למעלה בעלות טמפרטורה גבוה יותר מהמולקולות התחתונות, כך שקיים סך מעבר אנרגיה בכיוון החיובי של . התנגשויות בין המולקולות מגבירות את המעבר אנרגיה. נהוג גם לדבר על סך המעבר אנרגיה כתוצאה מתנועה רנדומלית כדיפוזיה של אנרגיה.

נהוג למדוד את תהליכי המעברי חום ע”י משוואות קצב מתאימות. בעזרת משוואות אלו ניתן לחשב את כמות האנרגיה שמועברת עבור יחידת זמן.

משפט:

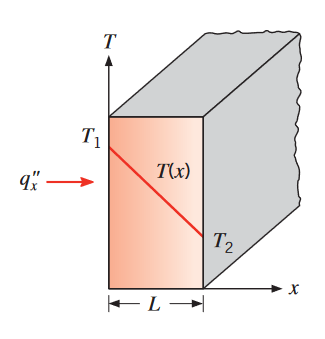
בהולכה, משוואת הקצב נקראת חוק פורייה. עבור מוט חד-ממדי, בעל פיזור טמפרטורה , משוואת הקצב היא:

כאשר:

• הביטוי נקרא שטף החום - קצב המעבר חום בכיוון ליחידת שטח, במאונך לכיוון מעבר החום.
• הביטוי הוא גרדיאנט הטמפרטורה בכיוון .
• הפרמטר נקרא המוליכות התרמית של החומר, והוא נמדד אמפירית.
  

מעבר חום חד ממדי ע”י הולכה (דיפוזיה של אנרגיה). (Bergman & Lavine, 2017).

במקרה התלת ממדי, חוק פורייה הוא מהצורה:

נשים לב שמשוואה זו נותנת את שטף החום. קצב המעבר חום בהולכה, , דרך משטח עם שטח הוא המכפלה של השטף והשטח:

דוגמה:

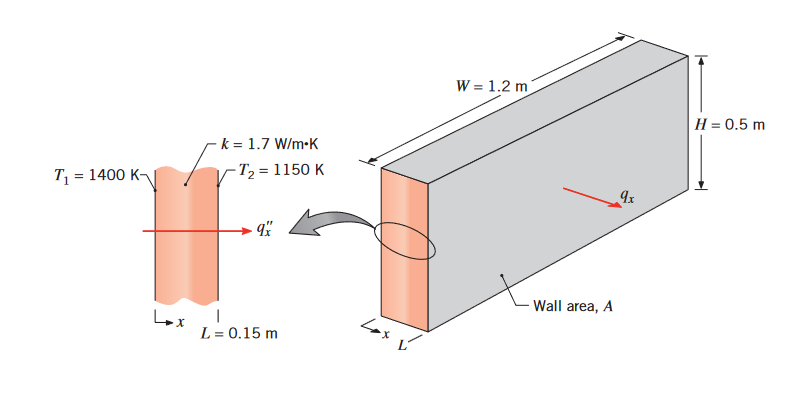
הקיר של תנור תעשייתי בנוי מקיר בטון בעובי , ועם מוליכות תרמית של . ממדידות במצב מתמיד מצאו כי הטמפרטורות הן ו- במשטחים הפנימיים והחיצוניים, בהתאמה. מהו קצב איבוד החום דרך הקיר, שבמדדים על הצד?

סכמת הבעיה. (Bergman & Lavine, 2017).

פתרון:
הנחות:

• מצב מתמיד.
• הולכה תרמית חד-מדדית דרך הקיר.
• הולכה תרמית קבועה.

מאחר ומעבר החום דרך הקיר הוא בהולכה, נוכל למצוא את שטף החום בעזרת חוק פורייה:

שטף החום הוא קצב מעבר החום דרך יחידית שטח, והוא אחיד לאורך משטח הקיר. לכן, קצב האיבוד חום דרך הקיר בעל שטח הוא:

ולכן:

הערה: סדר עם כל ה- -ים

בקורס נשתמש בסימונים כל הזמן וכל אחד מהם אומר משהו שונה, אבל יש היגיון מאחורי הסימונים האלו. בערך.

• הסימון הוא פשוט אינטראקציית חום כמו שאנחנו מכירים.
• הסימון הוא הספק, והוא ביחידות של .
• הסימונים הם כולם “נגזרות” של הספק לפי אורך. למשל, הוא הספק ליחידת אורך, והוא ביחידות של . הוא שטף החום ליחידת שטח והוא ביחידות של . הוא קצב ייצור חום נפחי, והוא ביחידות של .

הסעה

מנגנון ההסעה מובנה משני מכניזמים. מעבר למעבר אנרגיה כתוצאה מתזוזה רנדומלית של מולקולות (דיפוזיה), אנרגיה גם מועברת באופן מקרוסקופי, בעזרת תנועה של הזורם.

אנו בעיקר מעוניינים בהסעה בין זורם בתנועה ומשטח עם הפרשי טמפרטורות ביניהם. נביט למשל בזרימת זורם על משטח חם:

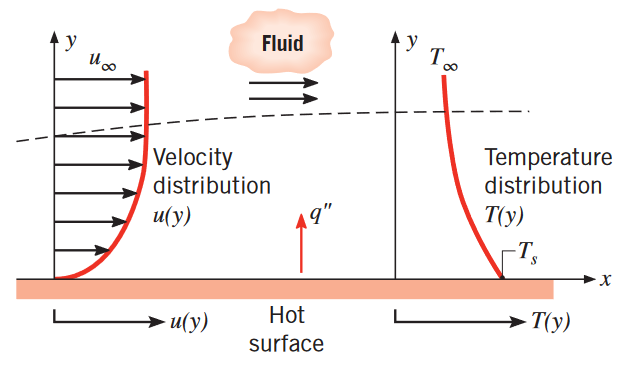
התפתחות שכבת גבול על משטח חם. (Bergman & Lavine, 2017).

מזרימה אנו יודעים שכך נראה פרופיל הזרימה של זורם על משטח - הוא בעל מהירות המשטח קרוב מאוד לקיר, ובעל מהירות סופית רחוק מהקיר. באותו אופן, ניתן להראות שליד הקיר לזורם טמפרטורה של הקיר, וטמפרטורה רחוק ממנו. לאזור בו שינוי זה מתרחש אנו קוראים שכבת גבול תרמית.

מאחר וליד הקיר תנועת הזורם ביחס למשטח היא אפסית, רוב מעבר החום מתרחש ע”י תנועה רנדומלית של המולקולות - דיפוזיה. התרומה של מעבר החום ע”י תנועה של הזורם מתרחשת יותר רחוק מהקיר, כאשר מהירות הזורם גדלה.

נהוג לסווג הסעה לפי גורם הזרימה. נאמר שההסעה מאולצת כאשר הזרם נוצר ע”י גורמים חיצוניים כמו מאוורר, משאבה, רוח וכו’ (ראו איור למטה, (a). הסעה טבעית לעומת זאת היא כאשר הזרם נגרם ע”י כוחות ציפה, שנגרמים כתוצאה מהפרשי צפיפויות, שנגרמים כתוצאה מהפרשי טמפרטורות בזורם.

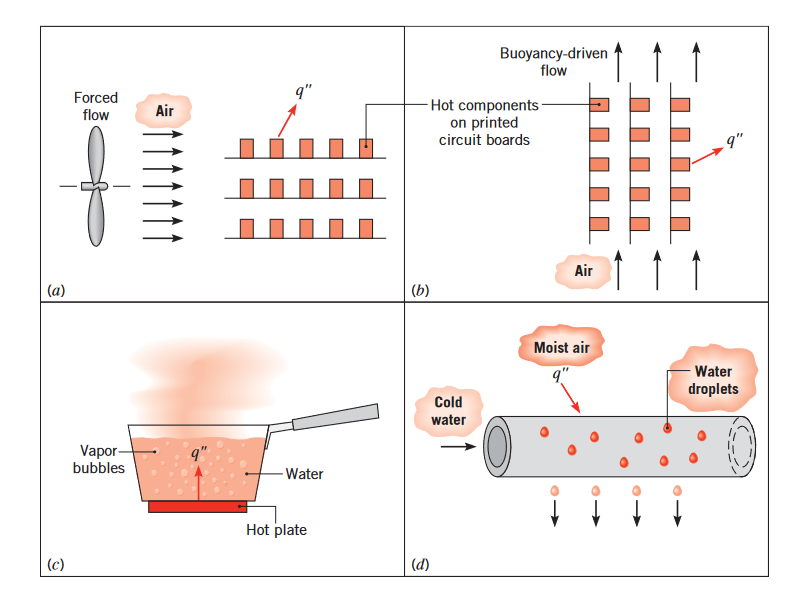
מעבר חום בהסעה. (a) הסעה מאולצת. (b) הסעה טבעית. (c) רתיחה. (d) התעבות. (Bergman & Lavine, 2017).

כמובן שרוב התהליכים הם למעשה שילוב של השניים. למשל אם בדוגמה עבור המאוורר באיור למעלה (a) האוויר ליד הרכיבים החשמליים מתחמם מספיק, הוא עלול לגרום לכוחות ציפה בכיוון המאונך לזרם הנגרם ע”י המאוורר, ובכך ליצור עוד זרם, הפעם בכיוון האנכי.

תיארנו את ההסעה כמעבר חום בזורם כשילוב של הולכה ותנועת זורם. בדרך כלל, האנרגיה שמועברת היא אנרגיה תרמית פנימית - אנרגיה של הזורם. אבל, בחלק מתהליכי הסעה, ישנו גם מעבר חום כמוס. מעבר חום זה הוא המעבר חום המתרחש כאשר ישנו שינויי פאזה בחומר. מקרים פרטיים מיוחדים הם רתיחה והתעבות.
למשל, הסעה מתרחשת כתוצאה מהבועות אדים הנוצרים בתחתית סיר מים רותחים (איור למעלה, (c)), או ע”י התעבות של אדי מים על השכבת החיצונית של צינור מים קר (איור למעלה, (d)).

משפט:

משוואת הקצב להסעה נקראת חוק הקירור של ניוטון, והיא קובעת כי:

כאשר:

• הביטוי הוא שטף החום כתוצאה מהסעה.
• הערכים ו- הם הטמפרטורות על המשטח והזורם, בהתאמה.
• הפרמטר תלוי בשכבת גבול (בעיקר בגאומטריה שלו), אופן הזרם, ומספר תכונות תרמודינמיות נוספות.
  כמוסכמה, המעבר חום חיובי אם הוא אל המשטח.

קרינה

קרינה תרמית היא אנרגיה שנפלטת ע”י כל חומר בטמפרטורה שהיא לא אפס. אנו בעיקר נעסוק בקרינה הנפלטת ממוצקים, אבל כמובן שהיא נפלטת גם מנוזלים וגזים. האנרגיה של הקרינה מונעת ע”י גלים אלקטרומגנטיים. בעוד המעבר של האנרגיה של הולכה או הסעה מצריך את הקיום של תווך חומרי מסוים, קרינה לא. למעשה, מעבר חום בקרינה מתבצע בצורה הכי יעילה בוואקום.

מקור הקרינה שנפלטת ממשטח הוא מהאנרגיה התרמית של המשטח, והקצב בו האנרגיה נפלטת ליחידת שטח () נקרא הספק הפליטה, .

משפט:

הקשר בין הספק הפליטה לטמפרטורת המשטח נקרא חוק סטפן-בולצמן, והוא קובע כי:

כאשר:

• הביטוי הוא הספק הפליטה.
• המקדם נקרא קבוע סטפן-בולצמן וערכו הוא:

• הפרמטר הוא תכונה של החומר הנקראת אמיסיביות, וערכה נע בין ל-.
• הביטוי הוא הטמפרטורה המוחלטת של המשטח (כלומר, הטמפרטורה שלו בקלוין ().

ישנו חסם עליון להספק הפליטה, והוא כאשר :

משטח בעל הספק פליטה זה נקרא גוף שחור.

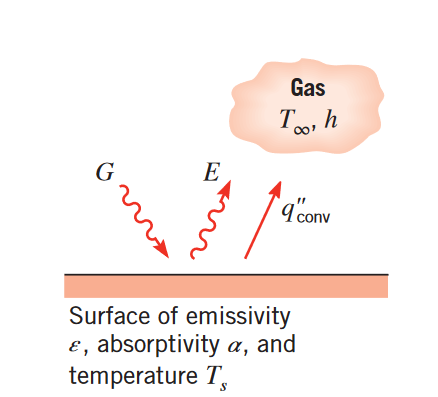
מעבר חום בקרינה ממשטח. (Bergman & Lavine, 2017).

קרינה עשויה להתרחש גם על משטח - למשל מהשמש או כל משטח אחר אליו המשטח המסוים חשוף אליו. אנו מגדירים את הקצב בו קרינה נקלטת ליחידת שטח כהקרנה .
חלק, או כל, מההקרנה על משטח עלולה להיספג ע”י המשטח, ובכך להעצים את האנרגיה התרמית של המשטח. הקצב בו אנרגיית הקרינה נספגת ליחידת שטח ניתנת להערכה מידע על תכונת המשטח הנקראת ספיגות:

כאשר . אם , והמשטח אטום, חלק מההקרנה מוחזרת. אם המשטח שקוף למחצה, חלק מההקרנה עלולה לעבור דרך המשטח.

הקשר לתרמודינמיקה

אנו יודעים מתרמודינמיקה שלמעברי חום תפקיד חשוב בחוק הראשון והחוק השני של התרמודינמיקה. בעוד בעזרת התרמודינמיקה אנו יכולים למצוא את כמות האנרגיה הדרושה עבור מערכת לעבור ממצב אחד למצב אחר, לא נוכל בעזרתו להבין את המכניזמים שמספקים את המעבר חום, או אפילו את חישוב קצב המעבר חום.
בקטע זה נקשר בין הכלים של מעבר חום לתרמודינמיקה.

הקשר לחוק הראשון של התרמודינמיקה

החוק הראשון של התרמודינמיקה קובע שסך האנרגיה של מערכת נשמרת, כאשר סך האנרגיה מורכב מאנרגיה מכנית ואנרגיה פנימית:

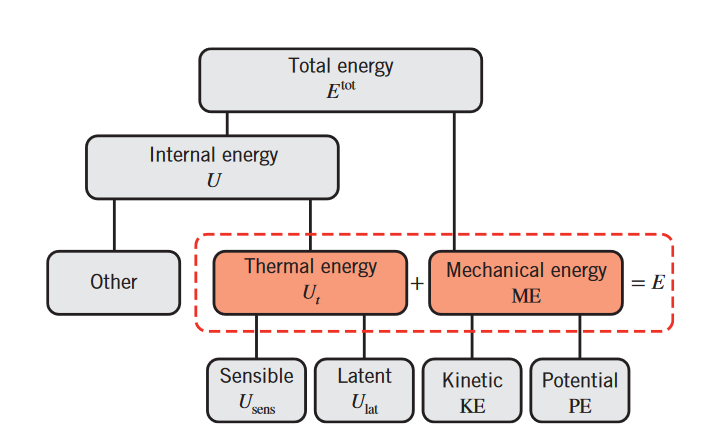
המרכיבים של סך האנרגיה. הסכום של האנרגיה התרמית והאנרגיה המכנית, , הוא עיקר העניין במעבר חום. (Bergman & Lavine, 2017).

האנרגיה המכנית מורכבת מאנרגיה קינטית ופוטנציאלית שאנחנו מכירים מפיזיקה. האנרגיה התרמית, שהיא חלק מהאנרגיה הפנימית , מורכבת מאנרגיה כמוסה (latent) ואנרגיה מוחשת (sensible) .
האנרגיה הכמוסה היא האנרגיה הקשורה לשינויים בפאזות של החומר, והאנרגיה המוחשת היא החלק שקשור בעיקר לשינויים בטמפרטורה (למרות שהיא יכולה להיות תלויה גם בלחץ).
למשל, אם מסה מסוימת עוברת מפאזה מוצקה לנוזלית, האנרגיה הכמוסה עולה. אם הטמפרטורה של המסה פשוט עולה, האנרגיה המוחשת שלה עולה.

עבור מערכת סגורה:

כאשר:

• הביטוי הוא השינוי בסך האנרגיה במערכת ( עבור stored).
• הביטוי הוא סך המעבר חום אל המערכת.
• הביטוי הוא סך העבודה שהתבצעה ע”י המערכת.
  

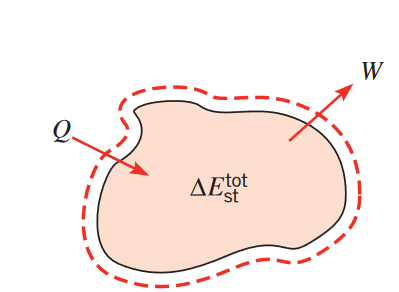
  שימור סך האנרגיה של מערכת סגורה בפרק זמן מסוים. (Bergman & Lavine, 2017).

את החוק הראשון נוכל ליישם עבור נפח בקרה (או מערכת פתוחה) - תחום במרחב המוגבל ע”י משטח הבקרה דרכו מסה יכולה לזרום. מסה הנכנסת ועוזבת את הנפח בקרה נושאת אנרגיה איתה. תהליך זה, הנקרא אדוקציה, מוסיף עוד ביטוי לחוק הראשון המתאר את האנרגיה שעלולה לעבור דרך גבולות הנפח בקרה. לכן, בדומה מאוד לפיתוח חוק ראשון בנפח בקרה, נפרק את השינוי באנרגיה לחלקים:

הציונים התחתונים ו- מתייחסים לאנרגיה הנכנסת ויוצאת, בהתאמה. סך האנרגיה המכנית והתרמית שנוצרת בנפח בקרה מיוצגת ע”י . נוכל לגזור כדי לקבל את הקשר:

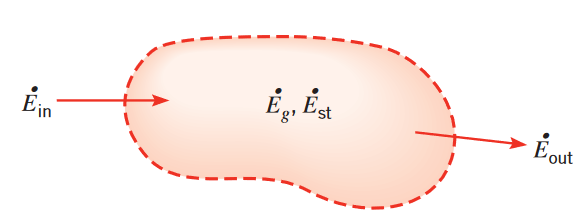
שימור אנרגיה תרמית ומכנית בנפח בקרה ברגע זמן מסוים. (Bergman & Lavine, 2017).

תרגילים

שאלה 1

תיבה העשויה פלדה במשקל מקבלת חום מהסביבה בשיעור של ולאחד מכן מבודדת היטב. התיבה נמצאת בטמפרטורה של . החום הסגולי של פלדה הינו קבוע וערכו . חשבו את הטמפרטורה של התיבה לאחר שהגיע לשיווי משקל.

פתרון:

לפי חוק ראשון:

נציב נתונים ונקבל:

שאלה 2

לשבב סיליקון מרובע () בעובי המונח בתוך מצע מבודד, כך שרק הדופן העליונה מקוררת ע”י זורם, מותקנים רכיבים חשמליים הממוקמים על הדופן התחתונה. הרכיבים מייצרים הספק חימום.

סכמת הבעיה

סעיף א’

מהו הפרש הטמפרטורות הנוצר בין הדופן העליונה והדופן התחתונה במצב מתמיד (מוליכות תרמית של סיליקון הינה ).

פתרון:
לפי חוק פורייה:

מאחר והשטף חום הוא :

נחשב את הפרש הטמפרטורות הדרוש:

נציב נתונים ונסיק כי:

סעיף ב’

טמפרטורת הזורם היא , וקיימת מגבלה על טמפרטורת הדופן העליונה להיות לכל היותר. יש לחשב את ההספק המקסימלי הניתן לסילוק משבב זה, כאשר:

1. הזורם הינו אוויר ומקדם מעבר החום בהסעה מאולצת הינו ?
2. הזורם הינו מים ומקדם מעבר החום ברתיחה הינו .

פתרון:

1. לפי חוק הקירור של ניוטון: נקבל שטף חום מקסימלי, ולכן הספק מקסימלי כאשר ההפרש בין ל- יהיה הכי גדול - כלומר כאשר :
2. באותו אופן, רק הפעם מקדם מעבר החום שונה:

שאלה 3

בעזרת משב רוח חם ניתן להסיר שכבת אדים אשר מצטברים על חלון זכוכית. הטמפרטורות על פני החלון הן ו- והמוליכות התרמית של הזכוכית הינה . טמפרטורת האוויר החם היא ומקדמי מעבר החום בהסעה בתוך החדר אל החלון הינו ובחוץ הינו . מצא את שטף החום דרך החלון, את עובי החלון, ואת טמפרטורות האוויר הרחק מהחלון בחוץ.

סכמת הבעיה.

לפי חוק הקירור של ניוטון:

בנוסף, מחוק פורייה:

במקרה פשוט זה פילוג הטמפרטורות הוא לינארי, כך שלמעשה:

יש לנו שלושה משוואות ושלושה נעלמים - . נציב נתונים ונקבל: