אור - קרינה אלקטרומגנטית
גל
גל הוא הפרעה (שינוי), לרוב מחזורית, המתפשטת במרחב. למשל, גל מים הוא הפרעה בגובה המים. לגל ארבעה מאפיינים עיקריים:
- אורך גל (
) - המרחק בין שתי נקודות מינימום/מקסימום של הגל. נמדד ביחידות אורך. - משרעת (אמפליטודה) (
) - גודל ההפרעה (מידת הסטייה) ביחס לקו הבסיס. - תדירות (
) - מספר התנודות שהגל מבצע ביחידת זמן. כלומר, מספר הפעמים שהגל מגיע למקסימום ביחידת זמן מוגדרת. נמדד ביחידות הרץ ( ). - מהירות הגל (
) - מוגדרת שמהירות התקדמות של נקודה מסוימת על הגל, וניתן לחשב אותה כך:
גל אלקטרומגנטי
גל אלקטרו מגנטי הוא גל המורכב משני גלים: גל חשמלי וגל מגנטי, הניצבים זה לזה. מהי המשמעות של גל חשמלי וגל מגנטי לא הכרחית לכאן. לפעמים גם נקרא לגל אלקטרומגנטית קרינה אלקטרומגנטית.
.jpg)
כל גל אלקטרומגנטי נע בריק במהירות האור:
ספקטרום הוא טווח של ערכים, ללא פערים או “חורים” למיניהם. הספקטרום האלקטרומגנטי הוא ספקטרום של האורכי גל השונים של הגלים האלקטרומגנטיים. “האור הנראה”, כלומר, האור שהעין האנושית מסוגלת לראות, מחולקת לצבעים - אדום,כחול,ירוק,צהוב… כל הצבעים האלו הם בעצם גלים אלקטרומגנטיים בעלי אורכי גל שונים.
למעשה, אור הוא גל אלקטרומגנטי, והאור הנראה הוא חלק מאוד קטן מהספקטרום האלקטרומגנטי.
.jpg)
תופעות שלא תאמו לפיזיקה הקלאסית
ספקטרום פליטה של גוף חם
כל גוף פולט קרינה. מטמפרטורה של

ככל שהטמפרטורה עולה, אורך הגל של הקרינה מוסט לכיוון אורכי גל קצרים יותר, כלומר, לכיוון תדירויות גבוהות יותר:
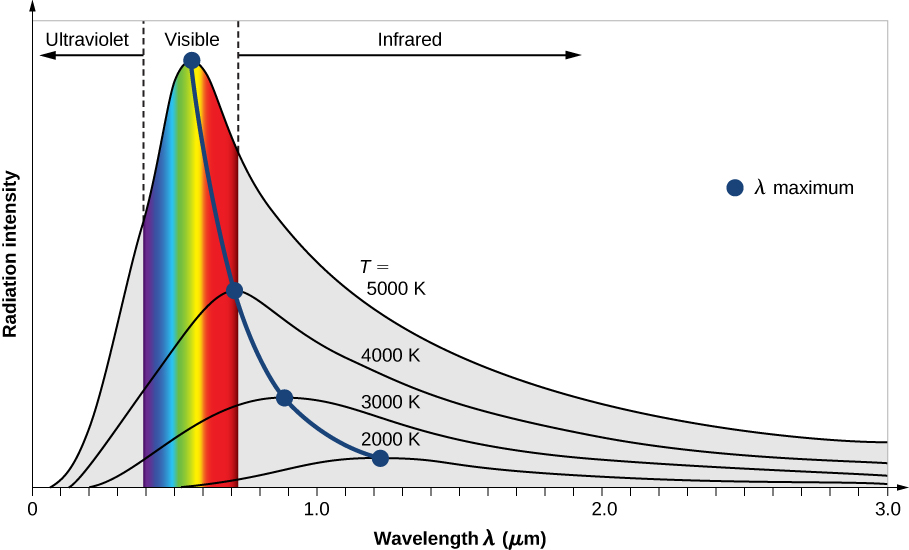
למשל, עבור
לכן עבור עצם עם טמפרטורה של

ישנה בעיה עם הגרף שהוצג. לפי הפיזיקה הקלאסית, פותחה נוסחה שאומרת כי ככל שאורך הגל,
.jpg)
ישנו עוד תרחיש שהפיזיקה הקלאסית לא יודעת להסביר:
האפקט הפוטואלקטרי
כאשר מקרינים משטח מתכתי באור, נפלטים מפני השטח שלו אלקטרונים.
.jpg)
מספר ניסויים שונים העידו על הממצאים הבאים:
- פליטת אלקטרונים מתחילה רק החל מתדירות סף מסוימת של האור (מסומן
). - האנרגיה הקינטית (או המהירות) של האלקטרון הנפלט פרופורציונלית לתדירות האור.
- מספר האלקטרונים הנפלטים פרופורציוני לעוצמת האור.
.jpg)
כלומר, גם אם נקרין על השטח המתכתי קרינה עם עוצמה ממש גבוהה, אך תדירות
ממצאים אלו נגדו לפיזיקה הקלאסית, שלפיה, האנרגיה הקינטית של האלקטרונים צריכה להיות תלויה בעוצמת האור.
ספקטרום אטומי
כאשר מביטים בספקטרום של האור הנפלט מהשמש (בעזרת מנסרת, המפזרת את האור לכלל מרכיביו), רואים ספקטרום רציף שכולל כל אורך גל. אך אם נבחן יותר בקפידות את ספקטרום זה, נגלה למעשה שהוא לא רציף, אלא בעל מספר “חורים”:
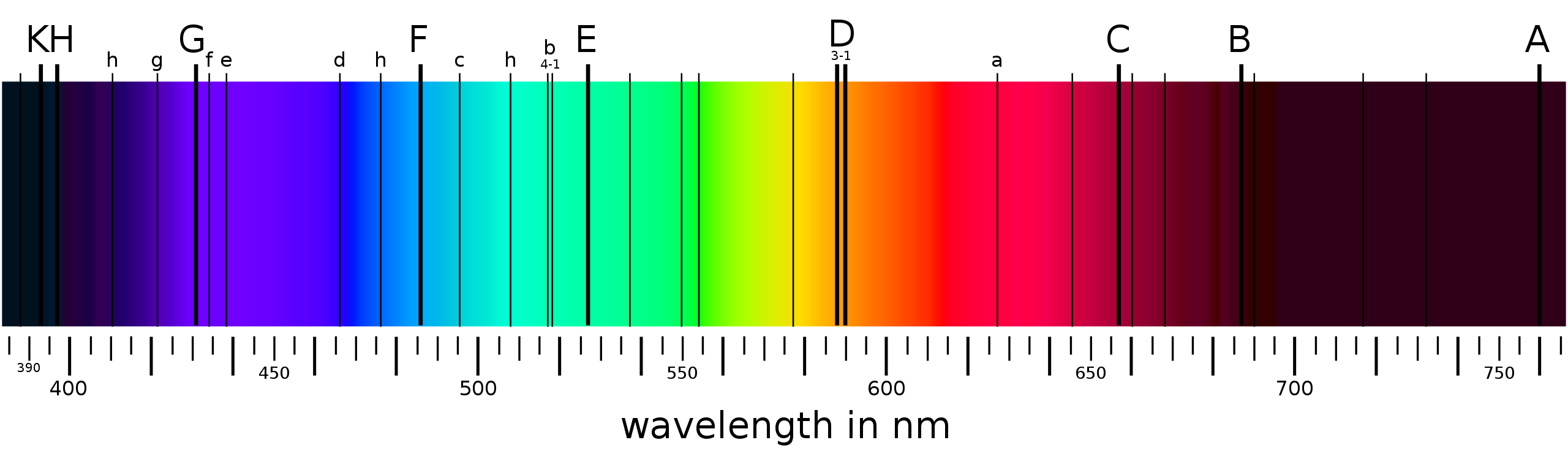
בנוסף, נסתכל על המערכת הבאה:
תחת חימום, גז הליום פולט קרינה. אם נביט על הספקטרום שלו, נגלה את ההפך:
.jpg)
קיבלנו רק סדרה מצומצמת ובדידה של פסים צרים שבינהם חלל שחור. כלומר, רק אורכי גל ספציפיים. עבור הליום, ישנם 5 קווים בספקטרום שהעין האנושית מסוגלת לראות. לכל יסוד יש קווים שונים, כך שהספקטרום האטומי שלו מהווה טביעת אצבע ייחודית שלו. בעזרת קווים אלו חוקרים יכולים לזהות יסודות רק מלפענח את שבירת הקרינה הנפלטת מהם על הספקטרום.
הספקטרום האטומי של מימן:
.jpg)
המודלים של הפיזיקה הקלאסית ושל האטום לא ידעו להסביר את תופעה זו.
התאוריה הקוונטית
בשנת 1900, כדי להסביר את העובדה שעוצמת הקרינה של גופים חמים לא גדלה ככל שתדירות הקרינה קטנה, הציע מקס פלאנק (1858-1947) רעיון מהפכני: אנרגיה היא לא ערך רציף. כאן, החצץ המבדיל בין פיזיקה קלאסית לפיזיקה קוונטית. הפיזיקה הקלאסית לא מגבילה את כמות האנרגיה שמערכת מסוימת יכולה להכיל, לעומת התאוריה הקוונטית, מגבילה אותו למספר מסוים של ערכים מסוימים. ההפרש בין שני ערכים מותרים של אנרגיה נקרא קוונט של אנרגיה. כאשר אנרגיה עולה מערך אחד לאחר, היא למעשה “קופצת” מערך אחד לאחר.
פלאנק הגיעה למסקנה שלקבוצת אטומים שנעים ביחד באותה תדירות על השטח פנים של גוף חם, יש האנרגיה הבאה:
כאשר
ניתן להכליל עוד יותר את המסקנה של פלאנק:
האנרגיה של קוונט של קרינה אלקטרומגנטית היא פרופורציונלית לתדירות שלה - ככל שהתדירות גבוהה יותר, כך ערך האנרגיה גדול יותר. הכללה זאת נקראת גם משוואת פלאנק:
בעזרת הרעיון שאנרגיה מקוונטת, פלנאק יכל לבנות משוואה חדשה שבעצם הצליחה לתאר באופן מדויק את הגרף של עוצמת הקרינה של גוף חם.
תאוריה זו גם ידעה להסביר את האפקט הפוטואלקטרי. ב-1905, אלברט אינשטיין הראה שאור לא מתנהג בהכרח כמו גל, אלא יש לו גם מאפיינים כמו של חלקיק. הוא טען שחלקיקים חסרי מסה של אור, הנקראים פוטונים, יש אנרגיה שנקבעת לפי משוואת פלאנק -
במודל חלקיקי של האור, אם פוטון פוגע באלקטרון, האלקטרון “קולט” את אנרגיית הפוטון. אם
דוגמאות:
- אנרגיית הסף של נחושת היא
. אם נקרין עליה אור בתדירות , אז: כלומר,
ולכן נפלט אלקטרון, בעל אנרגיה קינטית:
מודל האטום של בוהר
כדי להסביר את תופעת הספקטרום האטומי, בוהר בנה מודל עבור האטום מימן. הוא קבע כי:
- האלקטרונים נעים בתנועה מתמדת סביב הגרעין.
- לאלקטרון יש סדרה של מסלולים מעגלים מותרים, כאשר לכל מסלול רמת אנרגיה מסוימת.
- אלקטרון לא יכל להיות “בין” מסלולים - מותר לו להיות רק במסלול
-י כלשהו. במעברים בהם אלקטרון עובר ממסלול אחד לשני. האלקטרון קולט או פולט אנרגיה בגודל קבוע. המעבר הוא מיידי - הרי אסור לאלקטרון להיות בין שני מסלולים. כלומר האלקטרון “נעלם” ו”מופיע” מיד במסלול אחר.
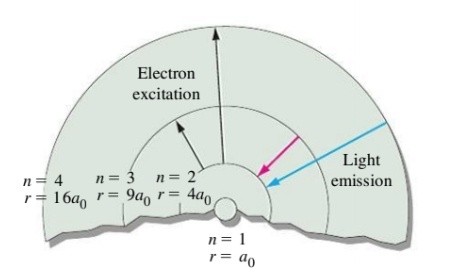
כדי לעבור ממסלול נמוך למסלול גבוה יותר (למשל מ-ל- ), האלקטרון צריך לקלוט אנרגיה. קליטה זו לרוב נעשית ע”י פוטון, המכיל את האנרגיה המדויקת הדרושה למעבר. כיוון שפוטון הוא מקוונט, אזי הוא צריך תדירות מדויקת בשביל המעבר.
באותו אופן, כאשר אלקטרון “יורד” למסלול נמוך יותר, הוא פולט פוטון בעל אנרגיה בהתאמה למעבר אותו הוא מבצע. כלומר, פולט פוטון בעל תדירות מדויקת.
המרחק של האלקטרון והגרעין גם כן תלוי ב-:
כאשר
נהוג להגדיר את האנרגיה של אלקטרון חופשי, כלומר לא “שייך” לאף גרעין, כאפס:
כאשר אלקטרון נמשך לגרעין אטום, ומשוייך לאחד ממסלוליו, אנרגיית האלקטרון הופכת לשלילית בעל ערך:
כאשר
כלומר, לכל מסלול יש רמת אנרגיה מדויקת. נוכל להציג את רמות האנרגיה אלו על גרף:
.jpg)
כברירת מחדל, האלקטרון יהיה במסלול
נבדיל בין שני מקרים:
- האלקטרון “בולע” אנרגיה - פוטון. לכן הוא עולה לרמת אנרגיה גובהה יותר בכך שהוא “בולע” פוטון עם תדירות מסוימת.
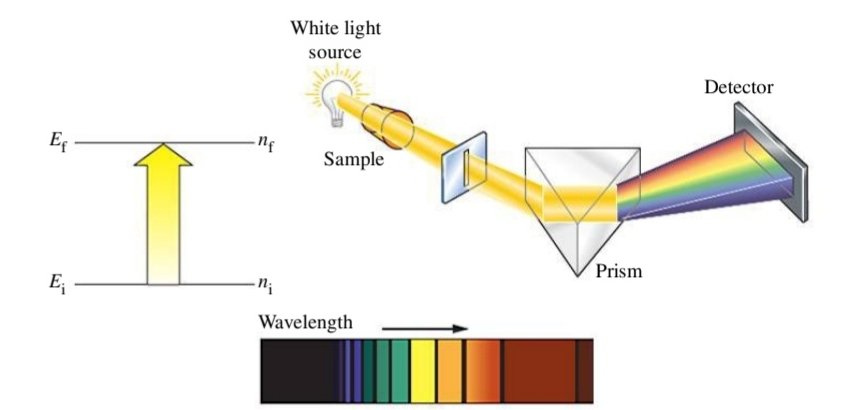
ניתן לראות כי אכן החומר “בולע” אור בעל רמות אנרגיה/תדירויות ספציפיות. - האלקטרון פולט אנרגיה - פוטון. כלומר, הוא יורד לרמת אנרגיה יותר נמוכה וכך פולט פוטון עם תדירות מסוימת.
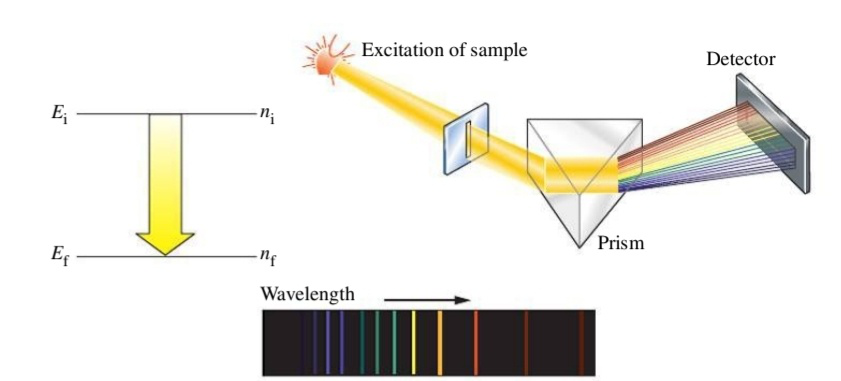
ניתן אכן לראות כי האלקטרון פלט קרינה בעלת תדירויות מסוימות (
נשים לב כי אורכי הגל הולכים ומצטמצמים. זה נובע מכך שרמות האנרגיה הולכות ומצטמצמות כפי שניתן לראות בגרף המראה את רמות האנרגיה השונות של מימן.
יינון אלקטרון
ניתן לחשוב על אלקטרון “חופשי” כאלקטרון בעל מסלול עם מרחק אינסופי מהגרעין. כלומר
כלומר, אם פוטון בעל אנרגייה
מודל בוהר מצליח להסביר את הספקטרום האטומי של אטומים אחרים בעלי אלקטרון יחיד, כמו
עבור אטומים אלו, האנרגיה של מסלולים שונים ניתנת ע”י:
כאשר
כשלי המודל
המודל האטומי של בוהר לא נכון. ישנם מספר כשלים, כמו למשל שהוא לא יודע להסביר את הספקטרום האטומי של אטומים בעלי יותר מאלקטרון אחד. בנוסף, המסלולים המתוארים במודלו של בוהר לא קיימים.
עם זאת, המודל היווה מקפצה מהתורה הקלאסית לתורה הקוונטית, ואין להזניח את חשיבותה.