| סטודנט א’ | |
|---|---|
| שם | עידו פנג בנטוב |
| ת”ז | 322869140 |
| דואר אלקטרוני | ido.fang@campus.technion.ac.il |
שאלה 1
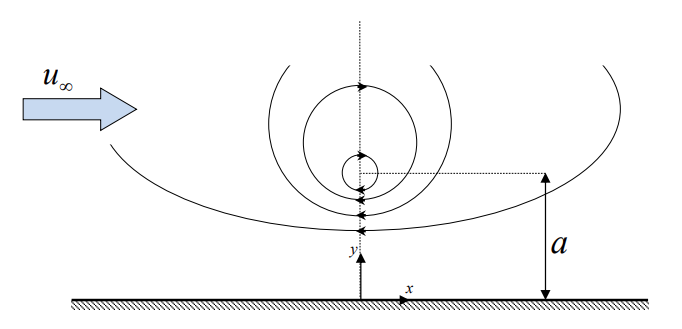
סכימת הערבול הזרימה המציפה
נשים לב כי החלפת משתנים הפוכה מפולאריות לקרטזיות היא:
סעיף א’
נוכל לתאר את פונקציית הפוטנציאל של שדה הזרימה המתואר כסופרפוזיציה של זרימות אלמנטריות. פוטנציאל של ערבול הממוקם ב-
פונקציית הפוטנציאל של זרימה מציפה:
הבעיה בשתי הזרימות הפוטנציאליות האלה הן שסכומן לא יקיים את תנאי האי-חדירה על הקיר. לפיכך, נשקף את הערבול מצידו השני של הקיר, בעוצמה הפוכה (נגד כיוון השעון), במרחק שווה (במיקום
נסכום:
נוודא שאכן תנאי האי-חדירה מתקיים:
ואכן, כאשר
כך שהתנאי אי-חדירה מתקיים.
עבור רכיב המהירות בכיוון
כאשר
בפתרון הרשמי מניחים ש-
סעיף ב’
נתון ששדה הזרימה אי-רוטוציוני, כך שנוכל להשתמש בברנולי בין כל שתי נקודות בשדה זרימה. נבחר נקודה כללית על הקיר, ונקודה רחוקה מהקיר:
רחוק מהקיר, כאשר
סעיף ג’
נבצע אינטגרציה לאורך
עבור האינטגרל השמאלי אנו ידועים איך לפתור מאינטגרלים מידיים. האינטגרל הימני דורש שיטות שלא למדנו:
לסיכום:
שאלה 2
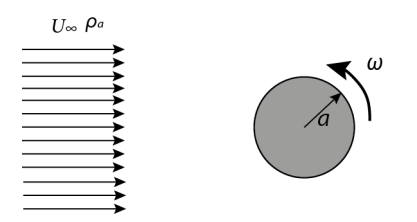
העפיפון ושדה הזרימה הנתונים
סעיף א’
בחירת מערכת הצירים
אנו יודעים שכדי לתאר את הבעיה הנתונה, נוכל לבצע סופרפוזיציה של זרימה מציפה, זוגן, וערבול:
מהחלפת משתנים
נמצא את המהירות הרדיאלית:
מתנאי אי-חדירה, אנו יודעים ש-
כלומר, כדי שתנאי אי-חדירה יתקיים, צריך להתקיים
נמצא את המהירות המשיקית:
נשים לב ש-
ולכן:
סעיף ב’
סכימת המצב המתואר
ניתן לראות מהאיור שמהירות הזרימה מעל הגליל תהיה גבוהה יותר מתחת לגליל. לפי ברנולי, אנו יודעים שכאשר המהירות גבוהה, הלחץ נמוך, כך שמתחת לגליל ישנו לחץ גבוה יותר מהחלק העליון של הגליל.
לפיכך, העפיפון ינוע כלפי מעלה.
סעיף ג’
כוח העילוי על הגליל:
מסעיף קודם, נסיק ששדה הזרימה הוא:
רחוק מהגליל (כאשר
על הגליל (כאשר
כיוון שהזרימה פוטנציאלית, נוכל לבצע ברנולי בכל המרחב, בפרט הרחק מהגליל, ועל הגליל:
נרצה למצוא את הכוח בכיוון
לחץ המופעל בנקודה כללית על שפת הגליל.
אכפת לנו רק מסך הכוח בכיוון
הפונקציה
שוב מופיע לנו קבוע כפול
מזהויות טריגונומטריות אנו יודעים ש-
במקרה בו
כוח הכבידה:
מהנתונים, נוכל להסיק שכוח הכבידה על כדור הוא פשוט:
השוואת הכוחות:
כדי שהעפיפון יישאר בגובה קבוע, נדרוש ששני הכוחות שווים אחד לשני:
שאלה 3
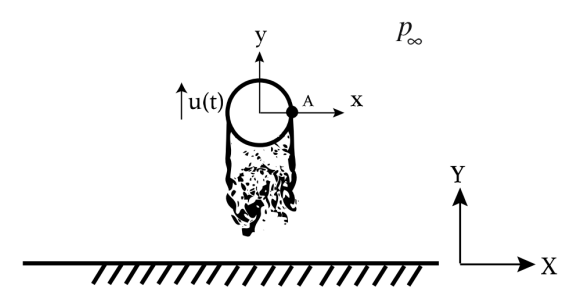
סכימת הגליל
סעיף א’
כדי לפתור את הבעיה בעזרת זרימה פוטנציאלית, צמיגות הזורם צריכה להיות זניחה (
סעיף ב’
באופן דומה ל[[#שאלה 2#סעיף א’|סעיף א’ בשאלה קודמת]], פונקציית הפוטנציאל תהיה סופרפוזיציה של זרימה מציפה וזוגן:
ההבדל מסעיף א’ בשאלה הקודמת הוא שכעת אין ערבול, וגם שהזרימה המציפה היא הפעם בכיוון
סעיף ג’
נפעל באותו אופן לפיתוח משוואת ברנולי שאנו מכירים, רק עם כמה טוויסטים. נתחיל ממשוואות אויילר:
נוכל להשתמש בזהות הבאה:
ואז נקבל:
בזרימה פוטנציאלית,
במערכת צירים צמודת הגליל, שהיא מערכת לא אינרציאלית, כוח הגוף שפועל על הגליל הוא מינוס התאוצה של המערכת צירים (הגליל). כלומר,
לכן:
מעצם הגדרת פונקציית הפוטנציאל, מתקיים
נכפיל את שני הצדדים ב-
כמו בפיתוח למשוואת ברנולי, נוכל לבצע “אינטגרציה” לפי מיקום
סעיף ד’
משוואת ברנולי שמצאנו ב[[#שאלה 3#סעיף ג’|סעיף ג’]] תקפה לכל שדה הזרימה ברגע
חישוב
מפתרון [[#שאלה 3#סעיף ב’|סעיף ב’]]:
לכן:
חישוב
מפתרון סעיף ב’:
ולכן:
נעלה בריבוע (נכפיל סקלרית בעצמו):
לכן:
נציב בפתרון בברנולי מ[[#שאלה 3#סעיף ג’|סעיף ג’]]. מצד אחד, אנחנו יודעים שעל הגליל:
מצד שני, ב-
נשווה:
באופן יותר מדויק:
בנקודה
סעיף ה’
נוכל לפרק את כוח העילוי על הגליל לשתיים - חלקו העליון וחלקו התחתון. כמו ב[[#שאלה 2#סעיף ג’|סעיף ג’ בשאלה קודמת]], נצטרך להטיל את הלחץ לכיוון
חלק מהאיברים נוכל לחבר לאינטגרל יחיד:
הפונקציה
נוציא קבועים:
ערכו של כל אינטגרל:
נציב בחזרה:
הערה:
כאן מתחיל ההבדל שלי מהפתרון הרשמי. משום מה אם המקדם של
הוא , ולא , מקבלים את הפתרון הרשמי. אבל אני יכול לומר די בוודאות ש- .
כיוון שאנו מזניחים כבידה, הכוח היחיד שפועל על הגליל הוא
ולכן:
זוהי מד”ר פרידה:
נציב תנאי התחלה
נציב בחזרה:
הפתרון תקף כל עוד
שאלה 4
סעיף א’
קו העקימון אינו
סעיף ב’
נפעל באותו אופן כמו בתרגול.
נרצה להשתמש במשוואת מקדם העילוי:
כאשר את
לכן, נחשב את הנגזרות של
באינטגרלים, אנו בהחלפת משתנים, ע”י ההתמרה:
נציב בנגזרות:
נרצה לדעת מהם גבולות התחומים במונחים של
נציב באינטגרלים:
נחשב על הדרך גם את
נוכל כעת למצוא את מקדם העילוי:
מהגדרת מקדם העילוי:
נדרוש
סעיף ג’
בסעיף קודם, מצאנו כי:
נציב
סעיף ד’
נציב פשוט בנוסחה למקדם המומנט ברבע מיתר:
ולכן:
סעיף ה’
נדרוש שסכום המומנט שנוצר ע”י כוח העילוי במרחק
נציב את הערכים שקיבלנו בסעיפים קודמים:
מרחק