| סטודנט א’ | |
|---|---|
| שם | עידו פנג בנטוב |
| ת”ז | 322869140 |
| דואר אלקטרוני | ido.fang@campus.technion.ac.il |
שאלה 1
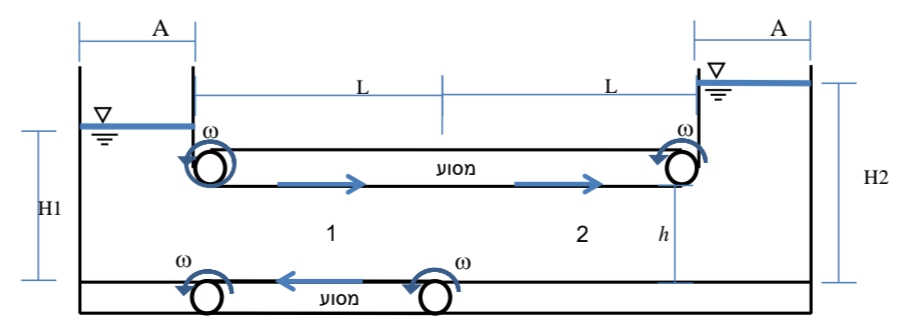
סכימת התעלה
סעיף א’
נבחר מערכת צירים קבועה בתחתית המסועה, בתחילתה:
בחירת מערכת צירים בתחתית המסועה
מהנתונים נניח את ההנחות הבאות:
- כיוון ש-
, נוכל להניח כי הגיאומטריה תמירה - השפעות הכבידה בתעלה זניחות (כי הגיאומטריה תמירה)
- הבעיה דו-ממדית
- מהירות שינוי גובה המיכלים קטנה משמעותית ממהירות הזורם בתעלה, כך שניתן לומר כי המצב מתמיד -
- הזרימה מפותחת -
.
סימון הביטול ל-
נניח גם את תנאי האי-חדירה ואי-החלקה (הזרימה צמיגה), כך ש:
ולכן:
- אין מהירות בכיוון האנכי -
.
לפי משוואות נאוויה-סטוקס הדו-ממדיות, בכיוון
בנוסף, אין כוחות גוף בכיוון
לפי משוואות נאוויה-סטוקס הדו-ממדיות, בכיוון
נישאר עם:
עבור שאר תנאי השפה, נתון כי אנו יכולים להניח פילוג לחץ הידרוסטטי במכלים. אבל, נשים לב כי
במקרים שלנו, עבור ההתחלה והסוף ישנם שני קבועים שונים:
ולכן בתחתית התעלה:
תנאי ההתחלה שלנו:
- במחצית הראשונה של התעלה:
- במחצית השנייה של התעלה:
סעיף ב’
את המהירויות בקצוות קל לשרטט מאחר והם פשוט תנאי השפה (מסעיף קודם).
מבחינת שאר הגבהים, נוכל להסיק מסופרפוזיציה של זרימת קואט וזרימת פואזיי (פרבולי):
פרופילי המהירות בשני האזורים
סעיף ג’
מסעיף א’, קיבלנו את המד”ח:
מאחר ו-
מהעברת אגפים:
את
אם נביט במשוואה
נמשיך באינטגרציה על
נגדיר את הלחץ בין שני האזורים כ-
- עבור אזור
עבור אזור
ולכן, באזור
נציב גם את התנאי שפה על המהירויות:
לכן, באזור
נציב את
נותר למצוא מהו
בחזרה ב-
נקבל ש:
ובאותו אופן עבור אזור
סעיף ד’
אנו נגיע למצב מתמיד כאשר הספיקה דרך אחד מהאזורים הוא
בהתחלה בכל מיכל הגובה הוא
משתי משוואות אלו נקבל:
שאלה 2
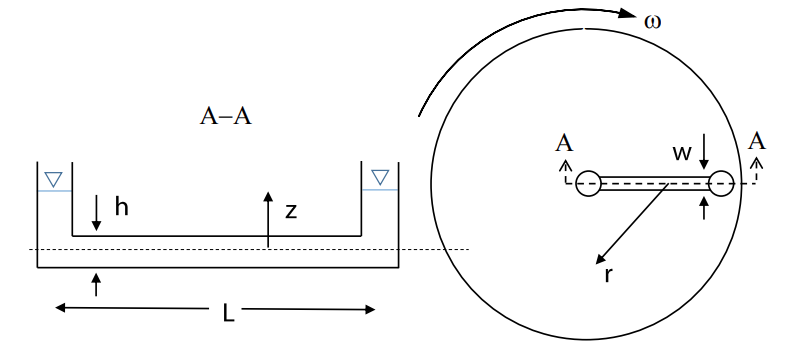
סעיף א’
נבחר את מערכת הצירים:
נניח את ההנחות הבאות:
- האינרציה זניחה
- גאומטריה תמירה (
- כבידה זניחה (עדיין יש כוחות גוף, הכבידה זניחה ביחס אליהם)
- בעיה דו ממדית
- הזרימה מפותחת -
לפי משוואת הרצף במקרה הדו-ממדי (עם
נסיק כי:
נוסיף ונאמר שמתקיים אי-חדירה, כך ש-
- מתקיים
ממשוואות נאוויה-סטוקס בכיוון
נישאר עם:
כוחות הגוף הם הכוחות הצנטריפוגליים (מערכת צירים לא אינרציאלית) -
כדי לקבל את המשוואה המנורמלת, ננרמל לפי גדלים אופייניים:
נציב במשוואה שקיבלנו:
אנו נרמלנו את הגדלים במשוואה, כך ש-
כדי לקבל את הגדלים האופייניים, נדרוש שכל המקדמים של הגדלים החסרי-ממד באותו סדר הגודל (כמו שהוסבר ב[[FLD1_006 צמיגות#שאלה 3#סעיף א’|שאלה בתרגול]]):
נקבל את הגדלים האופייניים:
נציב אותם בחזרה במשוואה ונקבל כי:
ממשוואות נאוויה-סטוקס בכיוון
ולכן, המשוואה הלא מנורמלת:
סעיף ב’
כדי שהאינרציה תהיה זניחה, נדרוש שמספר ריינולדס המוקטן יקיים
נציב את המהירות האופיינית מסעיף קודם (שמתקבל אם האינרציה זניחה):
סעיף ג’
מהמשוואה המנורמלת מ[[#שאלה 2#סעיף א’|סעיף א’]], נסיק כי המשוואה הלא מנורמלת היא:
כאשר הגדלים
אנו גם יודעים ש-
לפיכך, מאחר והם שווים, נסיק כי השוויון לעיל שווה לקבוע:
לפיכך:
נניח הידרוסטטיקה בשני המיכלים, כאשר גובה המיכל במרכז הוא
ולכן:
נחזור למשוואה:
נציב את
נעביר אגפים ונחלק ב-
נסמן את אגף ימין ב-
נניח תנאי-אי החלקה, כך שבעצם תנאי השפה שלנו הם:
ולכן:
נציב בחזרה את
כאשר גובה המים זהה, יתקיים:
אם מערכת הצירים שלנו הייתה ממוקמת באמצע הגובה של הצינור, היינו מקבלים את הפתרון הרשמי:
סעיף ד’
פרופילי המהירות בחתכים שונים
הראנו כבר שהזרימה מפותחת, כך שפרופיל המהירות זהה בכל החתכים.
סעיף ה’
נגיע למצב מתמיד כאשר הספיקה בתעלה תתאפס. כלומר, כאשר:
כאשר לא משנה באיזה חתך נבחר לחשב את
לכן הפרש הגבהים יהיה:
שאלה 3
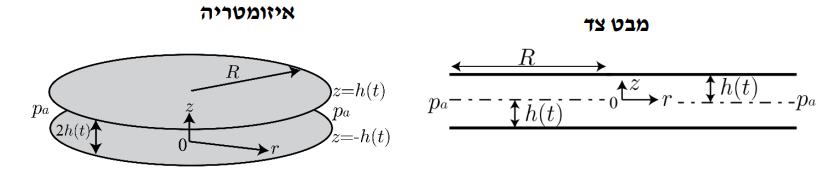
סכימת הפלטות
סעיף א’
נניח את ההנחות הבאות:
- כוחות גוף מוזנחים -
- הבעיה אקסיסימטרית -
- הלחץ תלוי רק בכיוון
- המהירות בציר
לפי משוואת הרצף:
ננרמל לפי:
נציב ונקבל:
הגדלים המנורמלים בסדר גודל
נציב נתונים התחלתיים ונקבל:
סעיף ב’
האינרציה זניחה אם
נציב נתונים ונמצא כי אכן:
\dfrac{ \partial }{ \partial t } \int _{V}\rho , \mathrm{d}V+\int _{\partial V} \rho \mathbf{q}\cdot \hat{\mathbf{n}} , \mathrm{d}A =0
\begin{gathered}
\dfrac{ \partial }{ \partial t } \int _{V} , \mathrm{d}V +\int _{\partial V}\mathbf{q}\cdot\hat{\mathbf{n}} , \mathrm{d}A=0 \[1ex]
\dfrac{ \partial V }{ \partial t } +\int _{\partial V}\mathbf{q}\cdot\hat{\mathbf{n}} , \mathrm{d}A =0 \[1ex]
\dfrac{ \partial V }{ \partial t } +\int {A}u{r} , \mathrm{d}A =0
\end{gathered}
\begin{aligned}
& V(t)=2\pi r^{2}h(t) \[1ex]
& \implies \dfrac{\mathrm{d}V}{\mathrm{d}t}= 2\pi r^{2}\dot{h}(t)
\end{aligned}
A=4\pi rh(t)
\begin{gathered}
2\pi r^{2}\dot{h}(t)+4\pi rh(t)\bar{u}{r}=0 \[1ex]
\boxed {
{\bar{u}}{r}=-\dfrac{r\dot{h}(t)}{2h(t)}
}
\end{gathered}
\begin{gathered}
\bar{u}{r}=\dfrac{1}{2h}\int{-h}^{h} u_{r} , \mathrm{d}z \[1ex]
\end{gathered}
\begin{gathered}
-\dfrac{r\dot{h}}{2h}=\dfrac{1}{2h}\int_{-h}^{h} u_{r} , \mathrm{d}z \[1ex]
-r\dot{h}=\int_{-h}^{h} u_{r} , \mathrm{d}z \[1ex]
\dot{h}=-\int_{h}^{h} \dfrac{u_{r}}{r} , \mathrm{d}z
\end{gathered}
f=\dfrac{u_{r}}{r}
\dot{h}=-\int_{-h}^{h}f , \mathrm{d}z
f=f(z,t)
\begin{aligned}
& \cancelto{ (5) }{ \rho\left( \dfrac{ \partial u_{r} }{ \partial t } +u_{r}\dfrac{ \partial u_{r} }{ \partial r }+u_{z}\dfrac{ \partial u_{r} }{ \partial z } +\dfrac{1}{r}\left( u_{\theta}\dfrac{ \partial u_{r} }{ \partial \theta } -{u_{\theta}}^{2} \right)\right) } \[1ex]
& =-\dfrac{ \partial p }{ \partial r }+\cancelto{ (1) }{ \rho g_{r} } +\mu\left( \dfrac{ \partial }{ \partial r } \left( \dfrac{1}{r}\dfrac{ \partial (ru_{r}) }{ \partial r } \right)+\dfrac{1}{r^{2}}\cancelto{ (2) }{ \dfrac{ \partial ^{2}u_{r} }{ \partial \theta ^{2} } } +\dfrac{ \partial ^{2}u_{r} }{ \partial z^{2} } -\dfrac{2}{r^{2}}\cancelto{ (2) }{ \dfrac{ \partial u_{\theta} }{ \partial \theta } } \right)
\end{aligned}
0=-\dfrac{ \partial p }{ \partial r } +\mu\left( \dfrac{ \partial }{ \partial r } \left( \dfrac{1}{r} \dfrac{\partial(ru_{r})}{\partial r} \right)+\dfrac{ \partial ^{2}u_{r} }{ \partial z^{2} } \right)
\dfrac{1}{r} \dfrac{ \partial }{ \partial r }(ru_{r}) =-\dfrac{ \partial u_{z} }{ \partial z }
\begin{gathered}
0=-\dfrac{ \partial p }{ \partial r } +\mu \dfrac{ \partial ^{2}u_{r} }{ \partial z^{2} } \[1ex]
\boxed {
\dfrac{ \partial p }{ \partial r } =\mu \dfrac{ \partial ^{2}u_{r} }{ \partial z^{2} }
}
\end{gathered}
0=-\cancelto{ (3) }{ \dfrac{ \partial p }{ \partial z } } +\mu\left( \dfrac{1}{r}\dfrac{ \partial }{ \partial r } \left( r \cancelto{ (4) }{ \dfrac{ \partial u_{z} }{ \partial r } } \right)+\dfrac{ \partial ^{2}u_{z} }{ \partial z^{2} } \right)
\boxed {
0=\mu \dfrac{ \partial ^{2} u_{z} }{ \partial z^{2} }
}
\boxed {
p(R)=p_{a}
}
\boxed {
u_{r}(h)=u_{r}(-h)=0
}
\dfrac{ \partial p }{ \partial r } =\mu \dfrac{ \partial ^{2}u_{r} }{ \partial z^{2} }
\begin{gathered}
\dfrac{ \partial p }{ \partial r } =\mu \dfrac{ \partial ^{2} }{ \partial z^{2} }(rf) \[1ex]
\dfrac{1}{r} \dfrac{ \partial p }{ \partial r } =\mu \dfrac{ \partial ^{2}f }{ \partial z^{2} }
\end{gathered}
\dfrac{1}{r}\dfrac{ \partial p }{ \partial r } =\mu \dfrac{ \partial ^{2}f }{ \partial z^{2} } =C(t) \tag{HW4.2}
\mu \dfrac{ \partial ^{2}f }{ \partial z^{2} } =C(t)
f=\dfrac{1}{2\mu}C(t)z^{2}+Az+B
\begin{aligned}
& f(h)=0: & & \dfrac{1}{2\mu}C(t)h^{2}+Ah+B=0 \[1ex]
& & & \implies B=-\dfrac{1}{2\mu}C(t)h^{2}-Ah \[3ex]
& f(-h)=0: & & \dfrac{1}{2\mu}C(t)h^{2}-Ah+B=0 \[1ex]
& & & Ah=\dfrac{1}{2\mu}C(t)h^{2}+B \[1ex]
& & & Ah=-Ah \[1ex]
& & & \implies A=0
\end{aligned}
\begin{aligned}
f & =\dfrac{1}{2\mu}C(t)z^{2}-\dfrac{1}{2\mu}C(t)h^{2} \[1ex]
& =\dfrac{1}{2\mu}C(t)(z^{2}-h^{2})
\end{aligned}
\dot{h}=-\int_{-h}^{h} f , \mathrm{d}z
\begin{gathered}
\dot{h}=-\int_{-h}^{h} \dfrac{1}{2\mu}C(t)(z^{2}-h^{2} ) , \mathrm{d}z \[1ex]
\dot{h}=-\dfrac{1}{2\mu}C(t)\left( \dfrac{2}{3}h^{3}-2h^{3}\right) \[1ex]
\dot{h}=\dfrac{2}{3\mu}C(t)h^{3} \[1ex]
C(t)=\dfrac{3\mu \dot{h}}{2h^{3}}
\end{gathered}
\dfrac{1}{r}\dfrac{ \partial p }{ \partial r } =C(t)
\begin{gathered}
\dfrac{1}{r} \dfrac{ \partial p }{ \partial r } =\dfrac{3\mu \dot{h}}{2h^{3}} \[1ex]
\dfrac{ \partial p }{ \partial r } =\dfrac{3\mu \dot{h}}{2h^{3}}r
\end{gathered}
p=\dfrac{3\mu \dot{h}}{4h^{3}}r^{2}+D
\begin{aligned}
& p(R)=p_{a}: & & \dfrac{3\mu \dot{h}}{4h^{3}}R^{2}+D=p_{a} \[1ex]
& & & D=p_{a}-\dfrac{3\mu \dot{h}}{4h^{3}}R^{2}
\end{aligned}
\begin{gathered}
p=\dfrac{3\mu \dot{h}}{4h^{3}}r^{2}+p_{a}-\dfrac{3\mu \dot{h}}{4h^{3}}R^{2} \[1ex]
\boxed{p=\dfrac{3\mu \dot{h}}{4h^{3}}(r^{2}-R^{2})+p_{a} }
\end{gathered}
\begin{aligned}
& \sum \mathbf{F}\cdot \hat{\mathbf{x}}=0: & & mg+2b\int_{0}^{L} \tau , \mathrm{d}x +b\int_{0}^{L} p_{0} , \mathrm{d}y-b\int_{0}^{L} p_{L} , \mathrm{d}y=0
\end{aligned}
mg+2\int_{0}^{L}\tau,\mathrm{d}x +\int_{0}^{L} {p}{0}-p{L} , \mathrm{d}y =0
L^{2}g\rho_{p}+2\int_{0}^{L} \tau , \mathrm{d}x +L({p}{0}-p{L})=0
L^{2}g\rho_{p}+2F_{sl}+L({p}{0}-p{L})=0 \tag{HW4.3}
\begin{gathered}
\cancelto{ (6) }{ \dfrac{ \partial u }{ \partial x } } +\dfrac{ \partial v }{ \partial y } =0 \[1ex]
v=\text{const}
\end{gathered}
v(0)=v(h)=0
\begin{aligned}
& \dfrac{ \partial p }{ \partial x } =\rho g+\mu \dfrac{ \partial ^{2}u }{ \partial y^{2} } \[1ex]
& \dfrac{ \partial p }{ \partial y } = 0
\end{aligned}
\dfrac{ \partial p }{ \partial x } =\rho g+\mu \dfrac{ \partial ^{2}u }{ \partial y^{2} } =\text{const}
p=Ax+b
\begin{aligned}
& p(0)={p}{0}: & & {p}{0}=b \[3ex]
& p(L)=p_{L}: & & p_{L}=AL+b \[1ex]
& & & p_{L}=AL+{p}{0} \[1ex]
& & & \implies A=\dfrac{p{L}-{p}_{0}}{L}
\end{aligned}
\dfrac{ \partial p }{ \partial x } =\dfrac{p_{L}-{p}_{0}}{L}
\begin{gathered}
\dfrac{p_{L}-{p}{0}}{L}=\rho g+\mu \dfrac{ \partial ^{2}u }{ \partial y^{2} } \[1ex]
\dfrac{ \partial ^{2}u }{ \partial y^{2} } =\underbrace{ \dfrac{p{L}-{p}{0}}{\mu L}-\dfrac{\rho g}{\mu} }{ K }
\end{gathered}
u=\dfrac{1}{2}Ky^{2}+{c}{1}y+{c}{2}
\begin{aligned}
& u(0)=0: & & {c}{2}=0 \[3ex]
& u(h)=U: & & \dfrac{1}{2}Kh^{2}+{c}{1}h+{c}{2}=U \[1ex]
& & & \dfrac{1}{2}Kh^{2}+{c}{1}h=U \[1ex]
& & & \implies {c}_{1}=\dfrac{U}{h}-\dfrac{1}{2}Kh
\end{aligned}
u=\dfrac{1}{2}K(y^{2}-hy)+\dfrac{U}{h}y
\tau_{xy}=\mu\left( \cancelto{ (7) }{ \dfrac{ \partial v }{ \partial x } } +\dfrac{ \partial u }{ \partial y } \right)
\tau_{xy}=\mu\left[ \dfrac{1}{2}K(2y-h) +\dfrac{U}{h}\right]
\tau_{xy}(h)=\mu\left( \dfrac{1}{2}Kh+\dfrac{U}{h} \right)
\begin{aligned}
F_{sl} & =-\int_{0}^{L}\tau_{xy}(h) , \mathrm{d}x \[1ex]
& =-L\mu\left( \dfrac{1}{2}Kh+\dfrac{U}{h} \right)
\end{aligned}
\begin{gather}
L\cancel{ ^{2} }g\rho_{p}-2\cancel{ L }\mu\left( \dfrac{1}{2}Kh+\dfrac{U}{h} \right)+\cancel{ L }({p}{0}-p{L})=0 \[1ex]
Lg\rho_{p}-\mu Kh-\dfrac{2\mu U}{h}+{p}{0}-p{L}=0 \[1ex]
p_{L}-{p}{0}=g\rho{p}L-\mu Kh-\dfrac{2\mu}{h}U
\end{gather}
\begin{gather}
K =\dfrac{p_{L}-{p}{0}}{\mu L}-\dfrac{\rho g}{\mu} \[1ex]
K=\dfrac{g\rho{p}}{\mu}-\dfrac{Kh}{L}-\dfrac{2}{Lh}U-\dfrac{\rho g}{\mu} \[1ex]
K =\dfrac{g}{\mu}(\rho_{p}-\rho)-\dfrac{h}{L}K-\dfrac{2}{Lh}U \[1ex]
K\left( 1+\dfrac{h}{L} \right)=\dfrac{g}{\mu}(\rho_{p}-\rho)-\dfrac{2}{Lh}U \[1ex]
\dfrac{K}{L}=\dfrac{g}{(L+h)\mu}(\rho_{p}-\rho)-\dfrac{2}{Lh(L+h)}U \[1ex]
K=\dfrac{gL(\rho_{p}-\rho)}{(L+h)\mu}-\dfrac{2U}{h(L+h)} \tag{HW4.4}
\end{gather}
\dfrac{ \partial }{ \partial t } \int _{V}\rho , \mathrm{d}V+\int _{\partial V}\rho \mathbf{q}\cdot\hat{\mathbf{n}} , \mathrm{d}A=0
\dfrac{ \partial }{ \partial t } \int {A}\rho , \mathrm{d}A+\int{\partial A}\rho \mathbf{q}\cdot\hat{\mathbf{n}} , \mathrm{d}\ell=0
\begin{gathered}
\dfrac{ \partial }{ \partial t } \int _{A} , \mathrm{d}A+\int _{\partial A}\mathbf{q}\cdot\hat{\mathbf{n}} , \mathrm{d}\ell=0 \[1ex]
\dfrac{ \partial A }{ \partial t } +\int _{\partial A}\mathbf{q}\cdot\hat{\mathbf{n}} , \mathrm{d}\ell=0
\end{gathered}
\begin{aligned}
& A=L(H(t)+L+2h)-L^{2} \[1ex]
& \implies \dfrac{ \partial A }{ \partial t } =L\dot{H}(t)
\end{aligned}
\dfrac{ \partial A }{ \partial t } =-LU
\begin{gathered}
-LU+2\int_{0}^{h} (u-U)\hat{\mathbf{x}}\cdot(-\hat{\mathbf{x}}) , \mathrm{d}y=0 \[1ex]
-LU+2Uh-2\int_{0}^{h} u , \mathrm{d}y =0 \[1ex]
U(2h-L)-2\int_{0}^{h} \dfrac{1}{2}K(y^{2}-hy)+\dfrac{U}{h}y , \mathrm{d}y =0 \[1ex]
U(2h-L)-K\left( \dfrac{1}{3}h^{3}-\dfrac{1}{2}h^{3} \right)-Uh=0 \[1ex]
U(2h-L)+\dfrac{1}{6}Kh^{3}-Uh=0 \[1ex]
U(L-h)=\dfrac{1}{6}Kh^{3}
\end{gathered}
\begin{gathered}
U(L-h)=\dfrac{h^{3}}{6}\left[ \dfrac{gL(\rho_{p}-\rho)}{(L+h)\mu}-\dfrac{2U}{h(L+h)} \right] \[1ex]
U(L^{2}-h^{2})=\dfrac{gLh^{3}(\rho_{p}-\rho)}{6\mu}-\dfrac{h^{2}U}{3} \[1ex]
U\left[ L^{2}-h^{2}+\dfrac{1}{3}h^{2} \right]=\dfrac{gLh^{3}(\rho_{p}-\rho)}{6\mu}
\end{gathered}
\begin{gathered}
UL^{2}=\dfrac{gLh^{3}(\rho_{p}-\rho)}{6\mu} \[1ex]
\boxed{U=\dfrac{gh^{3}(\rho_{p}-\rho)}{6\mu L} }
\end{gathered}