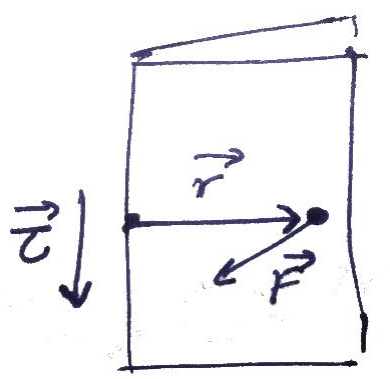
תנע זוויתי
ציטוט מגידי:
“תאמינו לי אני מסריח”.
אם לגוף יש מסה
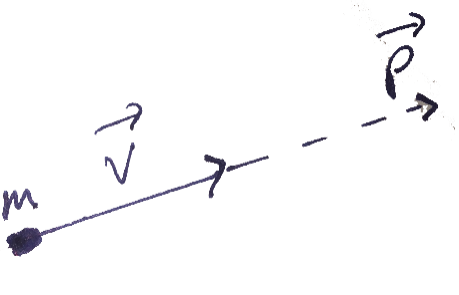
נשים לב שהמהירות של גוף אינה תלויה בבחירת ראשית הצירים במערכת ייחוס בה אנו עובדים. כלומר, עבור מערכת ייחוס נתונה, בחירה שונה של ראשית הצירים לא תשנה את המהירות שאנו מודדים. זה נכון משום שמהירות היא קצב שינוי ההעתק, וההעתק אינו תלוי בבחירת הראשית. מכאן שהתנע של גוף לא תלוי בבחירת ראשית הצירים של מערכת הייחוס בה אנו עובדים.
תנע זוויתי, לעומת זאת, תלוי בבחירת ראשית הצירים. נגדיר את ראשית הצירים,
הגדרה:
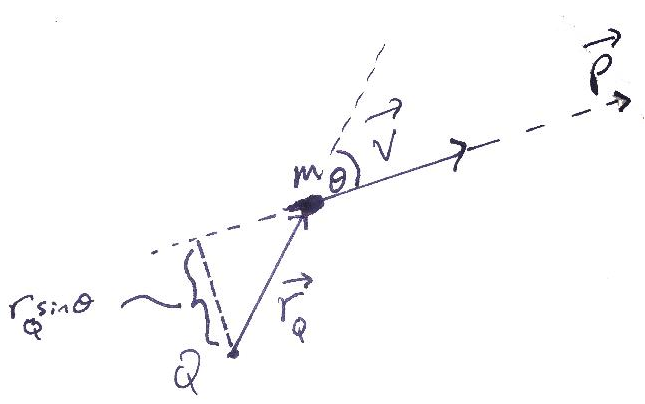
התנע הזוויתי ביחס לראשית הצירים שבחרנו מוגדר להיות הוקטור:
מה זה הפעולה
? מכפלה וקטורית יא מקדים פיזיקה. שמוק.
נשים לב שהתנע הזוויתי תלוי בבחירת ראשית הצירים. אלו נבחר את ראשית הצירים להיות בנקודה
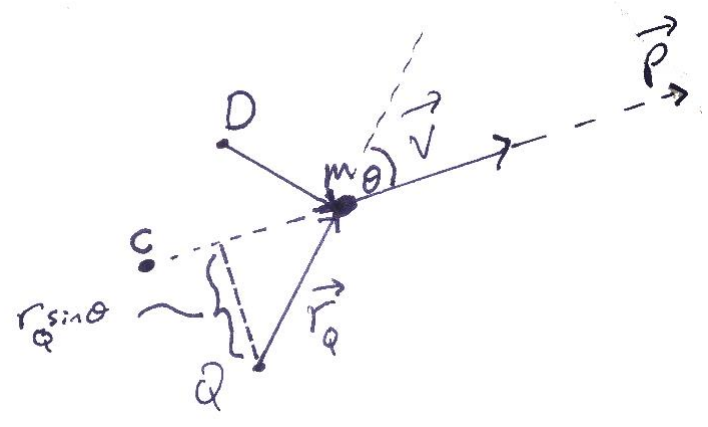
התנע הזוויתי יהיה
דוגמה:
נדון בתנועת כדור הארץ סביב השמש.
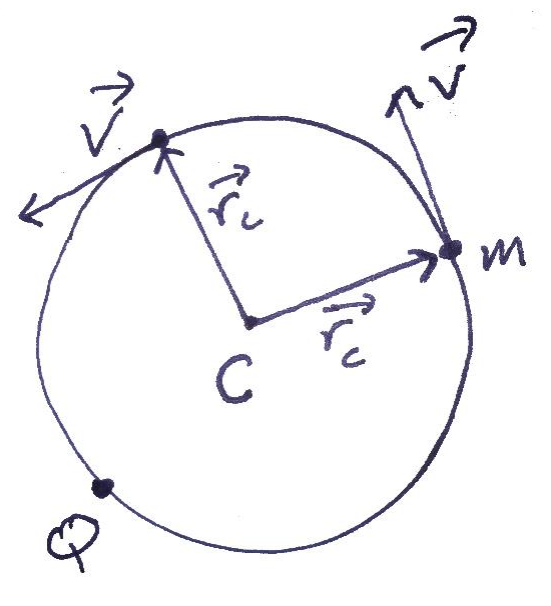
נניח שכדור הארץ נע במסלול מעגלי במהירות קבועה. בדוגמא זו גודל המהירות של כדור הארץ לא משתנה אך כיוון המהירות כן משתנה. מה התנע הזוויתי של כדור הארץ המסתובב סביב השמש ביחס לנקודה?
גודל התנע הזוויתי הוא:נשים לב שגודל התנע הזוויתי שווה בכל נקודה לאורך המסלול. זה נכון משום שהזווית בין וקטור המקום והמהירות הוא תמיד
. בנוסף, כיוון התנע זוויתי גם הוא קבוע ומצביע מחוץ ללוח. זוהי דוגמה בה המהירות משתנה כל הזמן, אך התנע הזוויתי אינו משתנה. נניח שהיינו בוחרים נקודת ראשית אחרת, בנקודה
באיור. האם התנע הזוויתי היה נשמר גם במקרה זה? במקרה זה התנע הזוויתי אינו נשמר. לדוגמא, יהיה רגע בו הגוף ינוע דרך הנקודה והתנע הזוויתי יתאפס (כי וקטור המקום ). בדוגמה זו התנע הזוויתי שמור רק ביחס לנקודה .
מומנט
בואו נתייחס באופן כללי לשאלה מתי התנע הזוויתי משתנה. שימו לב שבינתיים אנו מדברים רק על גוף נקודתי יחיד. התנע הזוויתי ביחס לנקודה
נזהה שהאיבר הראשון בצד ימין של המשוואה הוא:
משום שמכפלה וקטורית של וקטור עם עצמו מתאפסת. בנוסף, מחוק שני של ניוטון, הנגזרת של התנע הוא הכוח הכולל הפועל על הגוף:
מכאן נקבל ש:
כאשר:
הגדרה:
נגדיר את מומנט הסיבוב המופעל על ידי כוח
להיות: ניתן לכתוב משוואה זו בעזרת מומנט הסיבוב הכולל כ:
דוגמה:
נדמיין שאנו פותחים דלת. כאשר אנו מושכים את הדלת בידית אנו מפעילים כוח בכיוון ניצב לדלת. מכאן שהמומנט ביחס לציר הסביב של הדלת הוא:
וכיוונו במקביל לציר הסיבוב.
נדמיין שאנו מנסים לפתוח את הדלת על ידי הפעלת כוח ישירות על ציר הסיבוב. במקרה זה הדלת לא תפתח. מכיוון שהכוח מופעל על נקודת הייחוס שבחרנו, המומנט במקרה זה הוא. אנו יודעים מנסיון שככל שהידית רחוקה יותר מציר הסיבוב, קל יותר לפתוח את הדלת עבור שימוש בכוח נתון. במקרה זה גודל וקטור המקום גדל וכך גם המומנט. כלומר, זה אינו מספיק לדעת באיזה כוח מנסים לגרום לגוף להסתובב, צריך גם לדעת באיזה מרחק מציר הסיבוב אנו מפעילים כוח זה. מניסוי מחשבתי זה אנו רואים שהמומנט מרחיב את מושג הכוח כדי לתאר עד כמה הכוח גורם לגוף להסתובב סביב ציר סיבוב. במונחים של מומנט, ניתן לומר שככל שהמומנט גדול יותר, כך התנע הזוויתי של הגוף ישתנה בקצב גדול יותר.
מהביטוי שמצאנו אנו רואים שהתנע הזוויתי משתנה אם פועל מומנט כולל על הגוף. אם אין מומנט כולל, התנע הזוויתי נשמר. כלומר, ללא מומנט, התנע הזוויתי קבוע:
בדוגמה של כדור הארץ, הכוח תמיד מקביל לוקטור המקום (כוח הגרביטציה הוא כוח מרכזי ולכן פועל כלפי מרכז המעגל). במצב זה המכפלה הוקטורית בין וקטור המקום והכוח מתאפס (כי הסינוס במכפלה הוקטורית מתאפס). מכאן שבדוגמה זו אין מומנט הפועל על המערכת והתנע הזוויתי נשמר ביחס לנקודה
מומנט אינרציה
תנע זוויתי במסלול מעגלי
בתנועה מעגלית, המהירות הקווית של הגוף ניצבת לרדיוס שלו.

מכאן שגודל התנע הזוויתי ביחס לראשית הצירים הנמצאת במרכז המעגל היא:
שימו לב שגודל התנע הזוויתי נשאר קבוע לאורך כל תנועת הגוף. באופן כללי, עבור תנועה מעגלית מצאנו ש-
תוצאה זו מראה לראשונה את הקשר בין תנע זוויתי של גוף מסתובב למהירות הזוויתי שלו. בקרוב נדגים את החשיבות של קשר זה.
מה לגבי התנע הזוויתי? אם הגוף נע נגד כיוון השעון אז התנע הזוויתי הוא מחוץ למסך, והיפך, אם הגוף נע עם כיוון השעון. נהוג להגדיר את המהירות הזוויתית כוקטור,
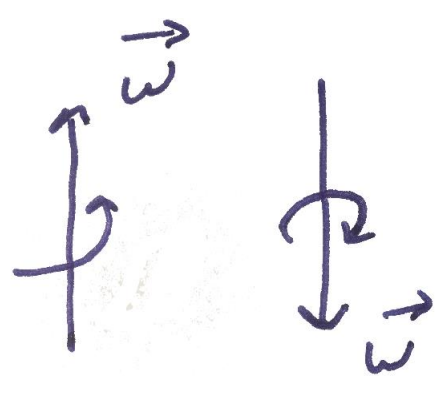
מכאן שהתנע הזוויתי בדוגמה של גוף יחיד מסתובב הוא:
נוסחה:
תנע זוויתי של מספר גופים בתנועה מעגלית
נניח שלושה גופים המחוברים אל ראשית הצירים דרך מוט חסר מסה. הגופים מסתובבים יחד במהירות זוויתית
מכיוון שלכל הגופים יש מהירות שונה אך מהירות זוויתי זהה, נוח לבטא ביטוי זה בעזרת הקשר
נגדיר:
הגדרה:
מומנט האינרציה של מערכת גופים הוא:
בעזרת הגדרה זו נקבל שהתנע הזוויתי הכולל של המערכת הוא:
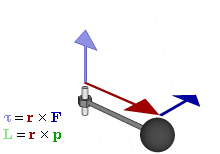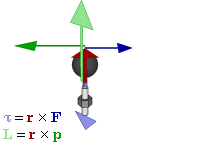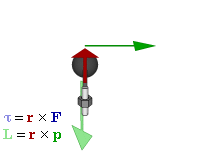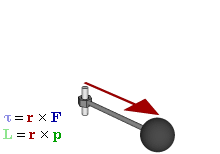
מומנט האינרציה מתאר את התפלגות המסה סביב ציר הסיבוב של גוף מסתובב. כפי שלמדנו, מסה היא תכונה פנימית של חומר שמתארת עד כמה כוח נתון יגרום למסה להאיץ. ככל שהמסה גדולה, כך כוח נתון יגרום למסה להאיץ פחות. נשים לב שגם אם נדע את המסה של גוף, זה לא מספיק לדעת עד כמה מומנט נתון יגרום לו להסתובב. לדוגמה, יהיה לי יותר קל לסובב את המשקולת המופיעה באיור במקרה השמאלי מאשר במקרה הימני.
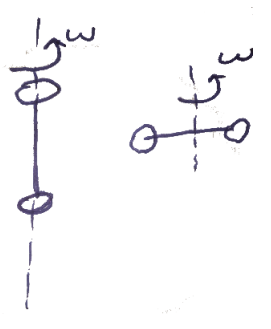
הסיבה היא שהתפלגות המסה סביב ציר הסיבוב השמאלי קטנה מזו של ציר הסיבוב הימני. ככל שהתפלגות המסה יותר קטנה סביב ציר הסיבוב, כך יהיה לי קל לסובב את הגוף. מומנט האינרציה הוא גודל המכמת את התפלגות המסה סביב ציר הסיבוב.
שילוב בין תנועה סיבובית לתנועה קווית
תנועה כללית של גוף כוללת גם תנועה קווית וגם סיבובית. נשים לב שגוף חופשי (
נניח כי הגוף נע ללא כוח חיצוני במישור הסיבוב שלו, מכאן שמהירות מרכז המסה במישור זה קבועה. כפי שרואים באיור למטה, אם הגוף לא יסתובב סביב מרכז המסה שלו (אנו דנים בגופים שטוחים אז מרכז המסה מתאר את ציר הסיבוב של הגוף), מהירות מרכז המסה תשתנה, דבר שאינו אפשרי.
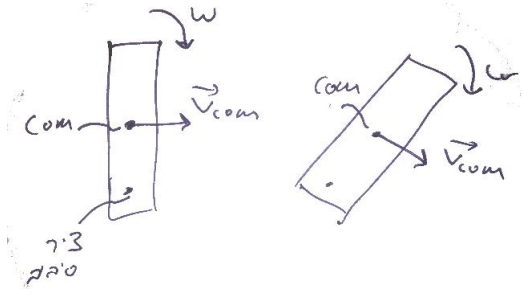
ניתן תמיד לתאר תנועת גוף כסכום של תנועת מרכז המסה והתנועה הסיבובית ביחס למרכז המסה. התנע הזוויתי במקרה כללי זה הוא:
בביטוי זה האיבר הראשון הוא התנע הזוויתי של מרכז המסה, והאיבר השני הוא התנע הזוויתי של הגוף סביב מרכז המסה.
אנרגיה קינטית של גוף הנע בתנועה קווית וסיבובית
ניתן לחשב את הסכום של האנרגיה הקינטית של כל הגופים:
הרבה פעמים יהיה יותר נוח לחשב את האנרגיה הקינטית בצורה השקולה:
האיבר הראשון בביטוי זה הוא האנרגיה הקינטית של מרכז המסה. האיבר השני הוא תרומה לאנרגיה הקינטית מסיבוב הגוף סביב מרכז המסה.