Introduction
From (Kalpakjian & Schmid, 2016):
Making a prototype, the first full-scale model of a product, has traditionally involved flexible manufacturing processes, such as machining operations, using a variety of cutting tools and machines, usually taking several weeks or months.
An important advance is rapid prototyping, also called three-dimensional printing or additive manufacturing, a process by which a solid physical model of a part is made directly from a three dimensional CAD drawing without the use of tools.
First developed in the 1980s, additive manufacturing involves several different processes and mechanisms, including resin curing, robot controlled extrusion deposition, melting and solidification, and sintering.
This section describes additive manufacturing, whereby parts are built in layers. Additive manufacturing inherently involves integrated computer-driven hardware and software. In order to visualize the methodology used, it is helpful to visualize constructing a loaf of bread by stacking and bonding individual slices on top of each other.
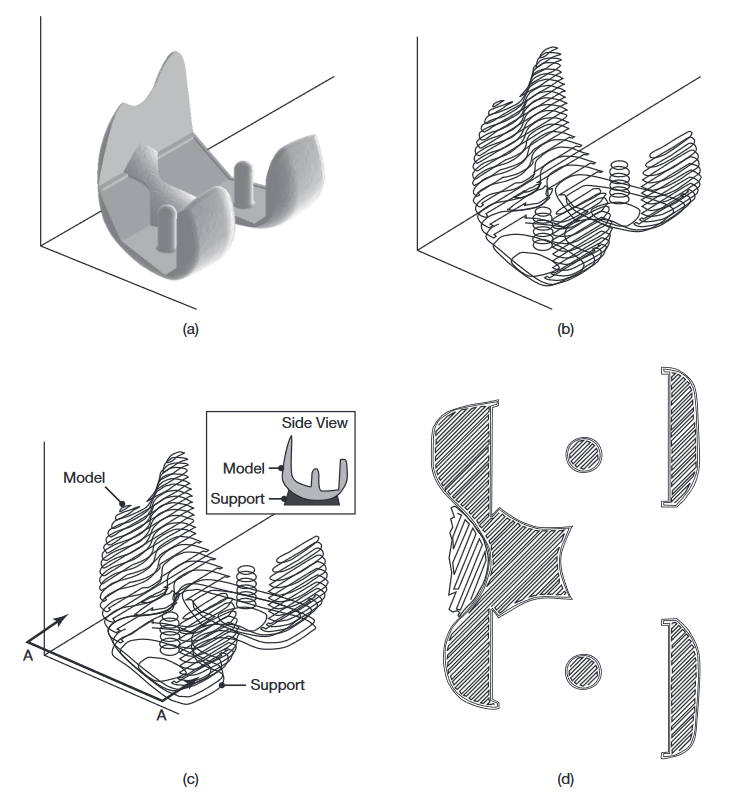
The computational steps involved in producing a stereolithography file. (a) Three-dimensional description of the part. (b) The part is divided into slices (only 1 in 10 is shown). (c) Support material is planned. (d) A set of tool directions is determined for manufacturing each slice. Shown is the extruder path at section A-A from (c), for a fused-deposition modeling operation. (Kalpakjian & Schmid, 2016).
Stereolithography
The stereolithography (STL) or vat photopolymerization process is based on the principle of curing (hardening) a liquid photopolymer into a specific shape. Consider what happens when a laser beam is focused on and translated across the surface of a liquid photopolymer. The laser serves to cure the photopolymer by providing the energy necessary for polymerization.

Schematic illustration of the stereolithography process. Source: 3D Systems.
Powder Bed Processes
Powder bed processes involve a number of processes that utilize powder as the workpiece material, and where the powder is deposited layer-by-layer in a bed or build chamber or cylinder.
Selective laser melting (SLM):
is a process based on selectively sintering of polymeric or metallic powders into an individual object; The basic components in this process are illustrated in the following figure:
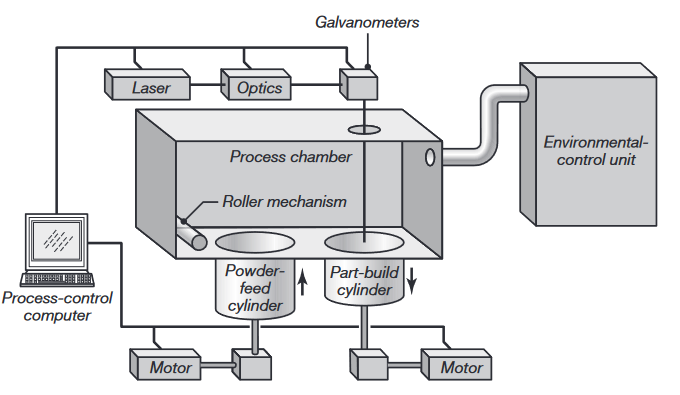
Schematic illustration of the selective-laser-sintering process. Source: C. Deckard and P.F. McClure.
In this process, a thin layer of powder is first deposited in the part-build cylinder. A laser beam, guided by a computer (using instructions generated by the 3D CAD program of the desired part), is then focused on that layer, tracing and melting a particular cross section, which then rapidly resolidifies into a solid mass (after the laser beam is moved to another section). The powder in other areas remains loose, but supports the solid portion. Another layer of powder is then deposited, and this cycle is repeated until the entire three-dimensional part has been produced.
Electron beam melting (EBM):
A process similar to selective laser sintering and electron-beam welding, electron-beam melting uses the energy source associated with an electron beam to melt metal powder (such as titanium, stainless steel, or cobalt-chrome) to make metal prototypes.
Diffusion in Powder Bed Processes
The diffusion processes in Electron Beam Melting (EBM) and Selective Laser Melting (SLM) can be described using equations from thermodynamics and materials science. We will focus on Arrhenius Equation:
Theorem:
The diffusion coefficient
is temperature-dependent and follows the Arrhenius relationship: where
is called the pre-exponential factor (related to the material); is the activation energy for diffusion (also related to the material); is the universal gas constant; and is the absolute temperature (in Kelvin).
This equation shows that diffusion rates increase exponentially with temperature, which is particularly relevant in high-temperature processes like EBM and SLM.
Another important concept is called the characteristic length of diffusion. it is Used to estimate the distance over which diffusion occurs within a certain period of time. It provides insight into how far particles, atoms, or molecules can move through a medium due to diffusion over a given timescale.
Definition:
The characteristic length
of diffusion is typically defined as the distance over which a diffusing species spreads in a material over a certain time . It is derived from the solution to Fick’s Second Law of Diffusion for certain boundary conditions. For a simple diffusion process in one dimension, the characteristic length can be estimated using the following relationship: where
is the Diffusion coefficient (rate of diffusion); and is the time over which diffusion occurs.
Energy Balance Equation for Powder Bed Processes
The energy balance equation is essential in understanding the thermal processes during Electron Beam Melting (EBM) in an ARCAM machine. This equation ensures that the energy supplied by the electron beam is correctly accounted for, influencing the melting, solidification, and cooling phases of the process.
The general form of the energy balance equation in an EBM system can be described as:
-
is the energy input from the electron beam: where
is the beam power (given in ), and is length of time the beam was powered. -
is the energy required to melt the powder from a solid to a liquid phase. It can be calculated as: where
is the mass of the material being melted, and is the Latent heat of fusion of the material, usually given in . -
includes the energy required to heat the material to its melting point. It can be calculated using the specific heat capacity of the material: where
is the temperature change (in Kelvin or Celsius).
Sometimes we also pass the boiling point of the material. In that case, we need to use two different specific heat capacities;for solid, and for liquid. is then given by: where
is the initial temperature; is the melting point temperature; and is the boiling point temperature.
Exercises
Question 1
Austenitic stainless steel 316 made pre-alloyed powder with particles size
If a layer of the material is exposed to a temperature of
The diffusion data of gamma-
The diffusion data of carbon atoms in gamma-
Part a
Estimate the expected minimal and maximal grain size in as-printed material through assumption that each particle size is a single-crystal.
Solution:
To find the grain size, we need to find the distance in which the diffusion occurred. We can do that using characteristic length of diffusion:
Do find
Substituting known parameters :
we get:
Therefore, the boundary of particle moved by
Part b
Estimate the expected size of undesired carbide precipitates which may be formed in the printed material through the process mentioned above.
Solution:
Just like the previous part, the increase in diameter
But now, we substitute the parameters for carbon:
We get that the characteristic length of an undesired carbide precipitate is:
Question 2
Based on energy balance equation, estimate the depth of the heat affected zone under the electron beam through EBM printing of Titanium sample in ARCAM machine wherein the beam scan velocity is
Assume that heat affected zone is in the shape of cylinder with diameter
Parameters:
Solution:
We can find the depth
The unknowns are
The total time can be given by:
And the mass is simply volume times density:
Substituting into the energy balance equation:
Using the given parameters, we get: