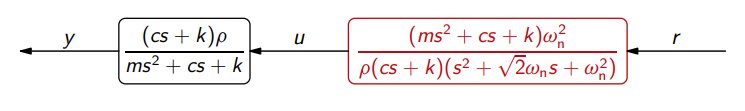מבוא
בהיפוך תהליך ראינו שבקר מושלם המניב
- לא ניתן למימוש במציאות
- עלול להיות מאוד לא יציב בגלל אי-יציבות פנימית.
נעסוק כעת באיך נוכל לדרוש
עבור בקר בחור פתוח מהצורה:
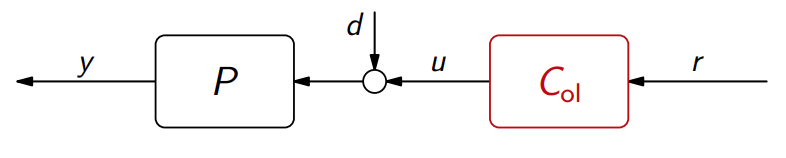
יש לתגובה שני מרכיבים בלתי תלויים:
- תגובה להפרעה
, שלא ניתן לשליטה ע”י הבקר . - תגובה לייחוס
שניתן לשליטה ע”י הבקר .
נעסוק במה שאנו כן יכולים לשלוט, הדינמיקה המבוקרת
והתגובות מצב מתמיד (steady-state) ומעבר (transient) שלו.
תגובה במצב מתמיד
יהי
אז השגיאה שלנו תהיה
כי התגובה במצב מתמיד של אות מדרגה תואם ל-
במילים אחרות, השגיאה שווה לגודל של התגובת תדירות של
נאמר שהשגיאה “קטנה” אם:
במקרים מסוימים יהיה יותר נוח לחשוב על טענה זאת כ
כי
מאחר ו-
שזה לא אותו הדבר כמו לדרוש
הערה:
אם אנו עובדים במערכות עם פרמטרים ממשיים, אז לדרישה
נצטרף להוסיף את הדרישה הצמודה . הסיבה לכך היא שהדרישה הראשונה אמנם מבטיחה לנו שהעוצמה של תהיה שווה לעוצמה של במצב מתמיד, אבל אין שום הבטחה על הפאזה שלה. ע”י הדרישה של הצמוד של , שהוא , בעצם אנו “מסדרים” את כך שגם הפאזה של תהיה שווה לפאזה של במצב מתמיד.
דוגמה:
אם
, כלומר , אז: מה שאומר שאנו צריכים לקבוע את ההגברה הסטטית
הנכון לבקר. למשל במקרה של מערכת מסה-גלגלת עם ריסון וקפיץ:
נבחרכי ההגברה הסטטית של מערכת זו היא
. הבקר הבא
הופך את, כך ש- :
ברור שהתגובת מעבר (transient response) היא לא מה שרצינו, אנחנו בכלל רצינו פונקציית מדרגה, אבל כן ענינו על הדרישה במצב מתמיד, ועוד יש לנו דרגת חופש עם
! אם כעת
, אז אמ”ם: נוכל לענות על דרישות אלו אם לכל
: ונמצא את
ו- ע”י הצבה בדרישות: נוכל לייצג זאת מטריצית:
שניתנת לפתרון לכל
.
במידה ו-, לכל , הבקר ב
הופך אתכך ש- :
ניתוח מודלי
נרצה לאפיין מערכות באופן איכותי ע”י מבט פשוט באפסים/קטבים שלהם. במקרים של מערכות מסדר ראשון או שני אנו מכירים כבר איך עושים זאת עם דיאגרמות בודה, אבל נביט קצת יותר לעומק בקטבים והאפסים ופרמטרים אחרים העלולים לעזור לנו בעזרת מה שנקרא ניתוח מודלי (modal analysis).
ניתוח מערכות מסדר ראשון ושני
במקרה של מערכת מסדר ראשון:
יש לה קוטב אחד ממשי ב:
כאשר
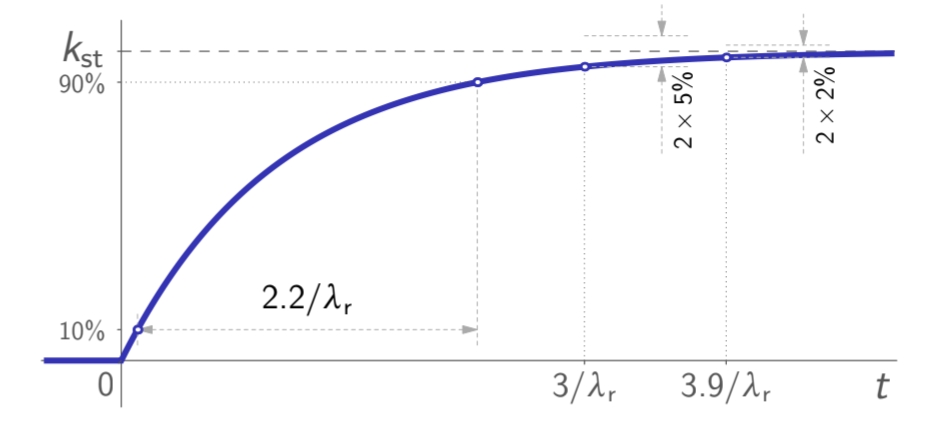
תגובת מדרגה של מערכת מסדר ראשון. (Leonid Mirkin’s Homepage, n.d.).
נשים לב שככל ש-
עבור מערכת מסדר שני תת מרוסנת עם פונקציית תמסורת מהצורה:
עם הקטבים ב
כאשר
כלומר:
- היחס בין החלקים הממשיים והמדומים של הקוטב תלוי רק ב-
. - הערך המוחלט של הקוטב תלוי אך ורק ב-
.
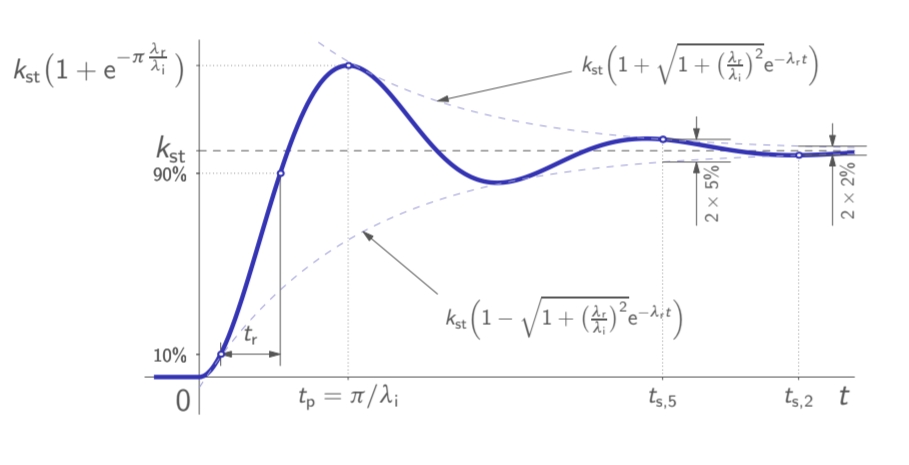
תגובת מדרגה של מערכת מסדר שני תת-מרוסנת. (Leonid Mirkin’s Homepage, n.d.).
נראה כי:
- ככל שהיחס
יותר גדול, כך התגובת יתר (overshoot) יותר נמוכה. - המהירות של התגובה פרופורציונלית לערך המוחלט של הקטבים.
הערה:
נשים לב שממשפט הערך ההתחלתי השיפוע ההתחלתי של מערכת עם הפרש קטבים ואפסים שגדול מ-
הוא תמיד , עבור כניסת מדרגה.
רמות תגובות יתר ותדירות טבעית
מהגרף של תגובת מדרגה של מערכת מסדר שני לעיל אנו רואים שעבור יחס
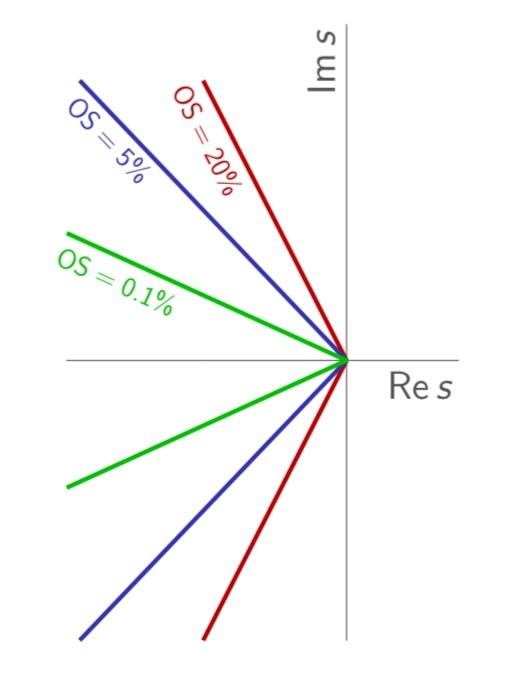
קווים רדיאליים של תגובות יתר קבועות. (Leonid Mirkin’s Homepage, n.d.).
אם נרצה לדרוש תגובה יתר מקסימלית
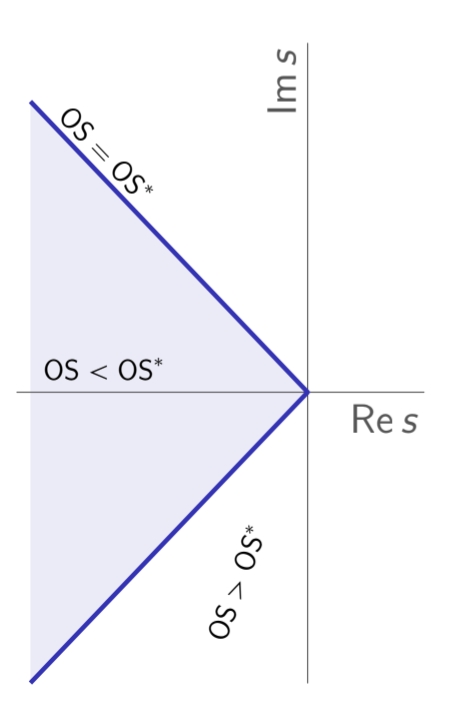
האזור במישור המרוכב עבורו הקטבים יקיימו
. (Leonid Mirkin’s Homepage, n.d.).
הערה:
רמת המקדם ריסון
הם אותם קווים רידאליים.
נשים לב גם שתדירות טבעית
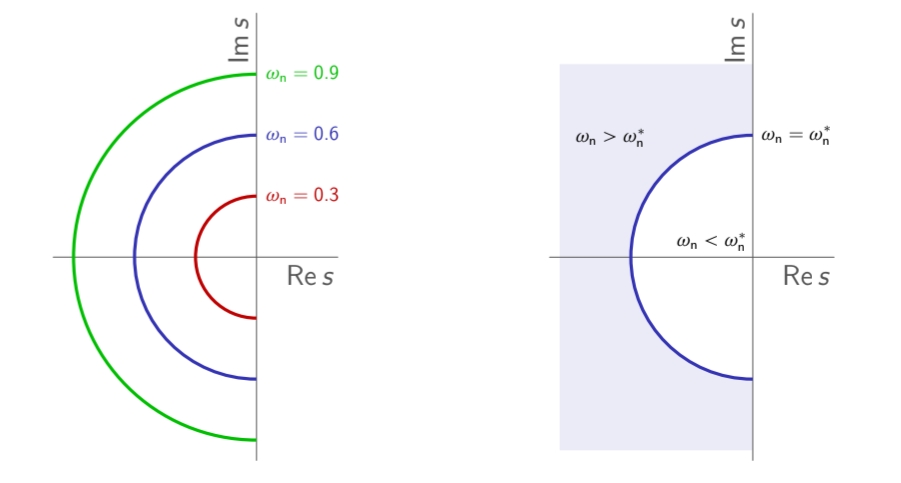
האזור במישור המרוכב עבורו הקטבים יקיימו
. (Leonid Mirkin’s Homepage, n.d.).
כעת, כדי לדרוש תגובה מעבר שהיא גם יחסית מהירה (
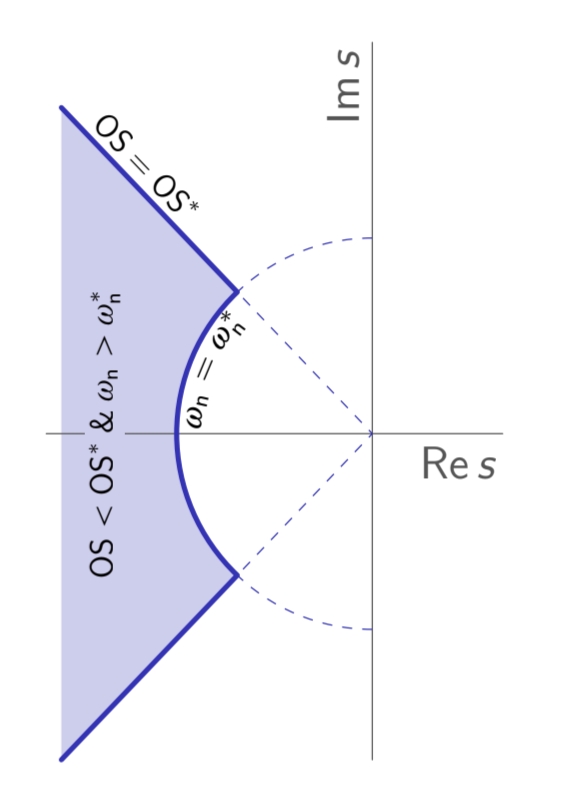
האזור בו כל הקטבים ממקומים כדי ליצור תגובות מדרגה “מהירות מספיק” ו”חלקות מספיק”. (Leonid Mirkin’s Homepage, n.d.).
השפעה של קוטב נוסף ואפס נוסף
יהי
עבור

ניתן לחשוב על התגובה של
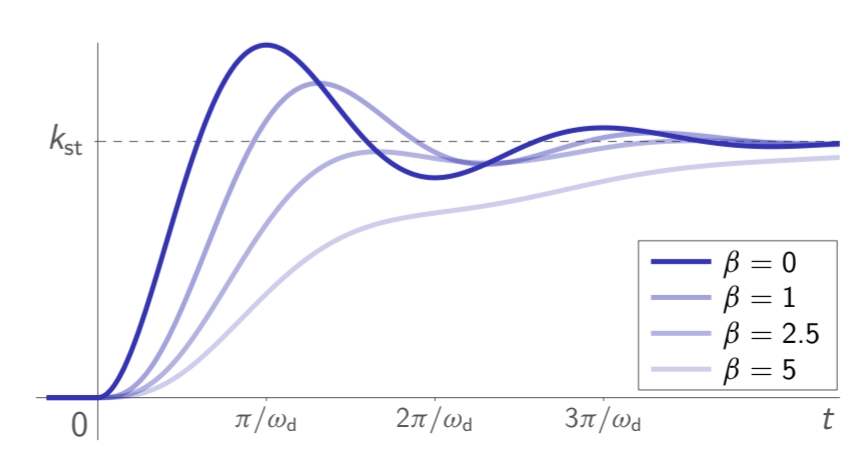
התגובה של
עבור ערכים שונים של , כאשר שקול למערכת מסדר שני. (Leonid Mirkin’s Homepage, n.d.).
נשים לב שככל ש-
- התגובת יתר
קטנה. - הזמן עלייה (raise time) עולה.
נביט כעת בהשפעה של אפס נוסף על המערכת. יהי:
עבור
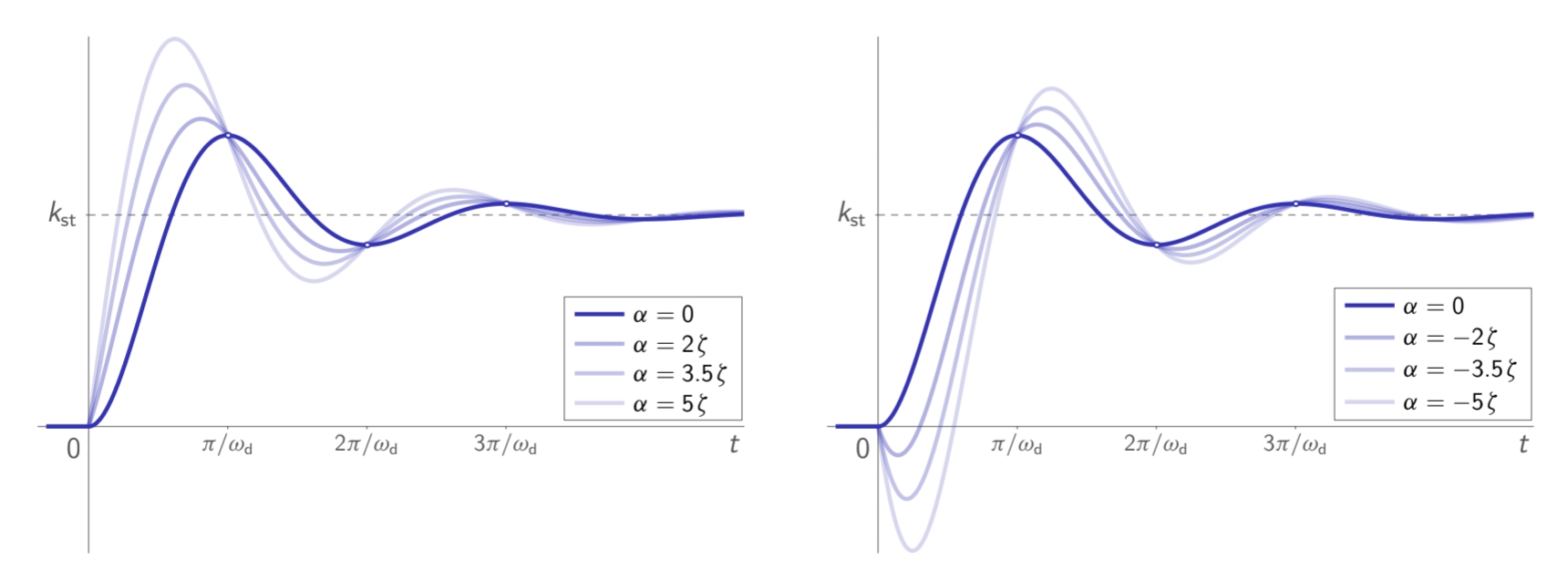
תגובת מדרגה ל-
עבור ערכים שונים של , כאשר המערכת מסדר שני הבסיסית היא תת-מרוסנת. (Leonid Mirkin’s Homepage, n.d.).
ככל ש-
- התגובת יתר
גדלה. - התגובת חסר (undershoot)
גדלה. - הזמן עלייה
קטן. - הזמן רגיעה
גדל.
במידה והמערכת מסדר שני הבסיסית מרוסנת-יתר:
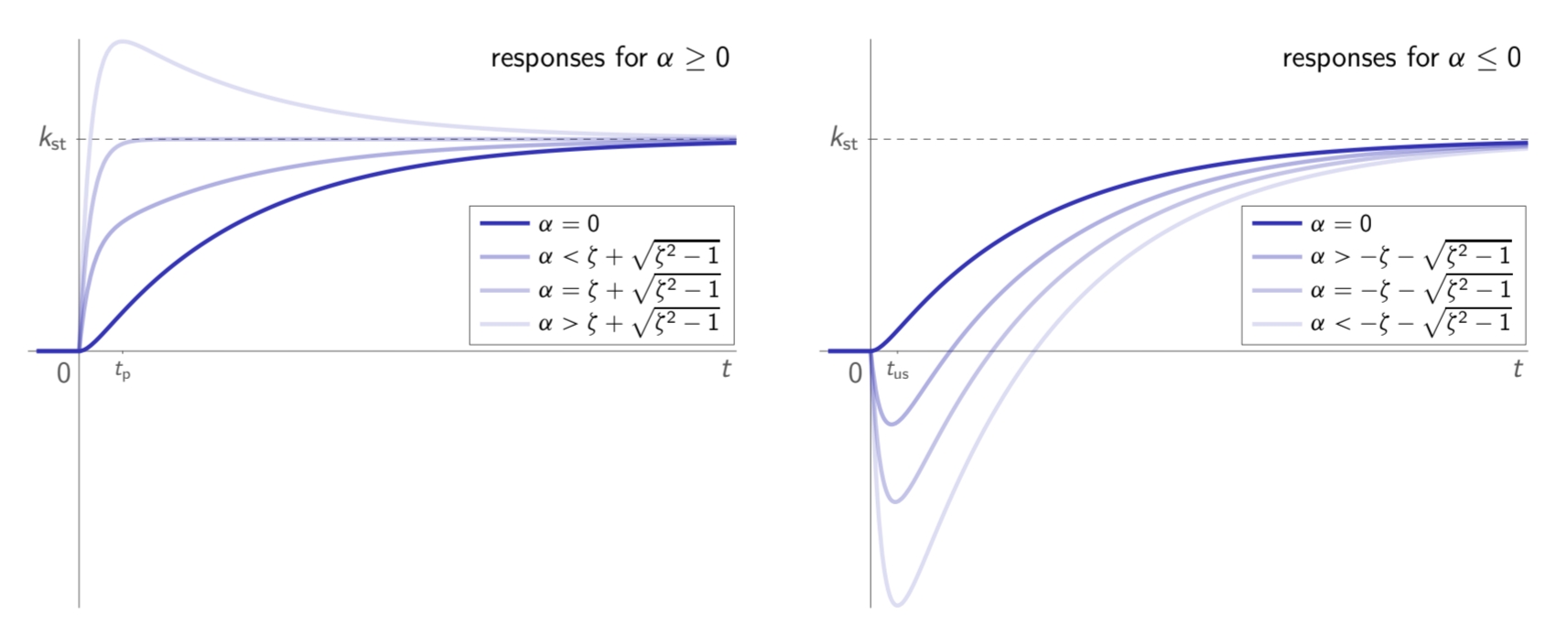
תגובת מדרגה ל-
עבור ערכים שונים של , כאשר המערכת מסדר שני הבסיסית היא מרוסנת-יתר. (Leonid Mirkin’s Homepage, n.d.).
ככל ש-
- התגובת יתר
גדלה, במידה ו- . - התגובת חסר
גדלה, במידה ו- . - הזמן עלייה
קטן.
ראינו כעת שבעוד ניתוח מודלי עובד טוב למערכות מסדר ראשון ושני, הוא כושל במקרים בהם מוסיפים למערכות אלו קטבים ואפסים נוספים. למשל, עלולה להיות לנו תגובת יתר למערכות רק עם אפסים/קטבים ממשיים.
אבל, במקרים מסוימים, נוכל להרחיב את הניתוח המודלי למערכת מסדר גבוה יותר אם הדינמיקה הדומיננטית של המערכת היא מסדר נמוך.
דינמיקה דומיננטית
הגדרה: אפס/קוטב דומיננטי
נאמר שקבוצה של אפסים/קטבים הם דומיננטיים אם אחת מהטענות הבאות תקפות:
- כלל האפסים/קטבים האחרים רחוקים בלפחות פי
מהציר המדומה . - האפסים/קטבים הקרובים “כמעט מבטלים” אחד את השני.
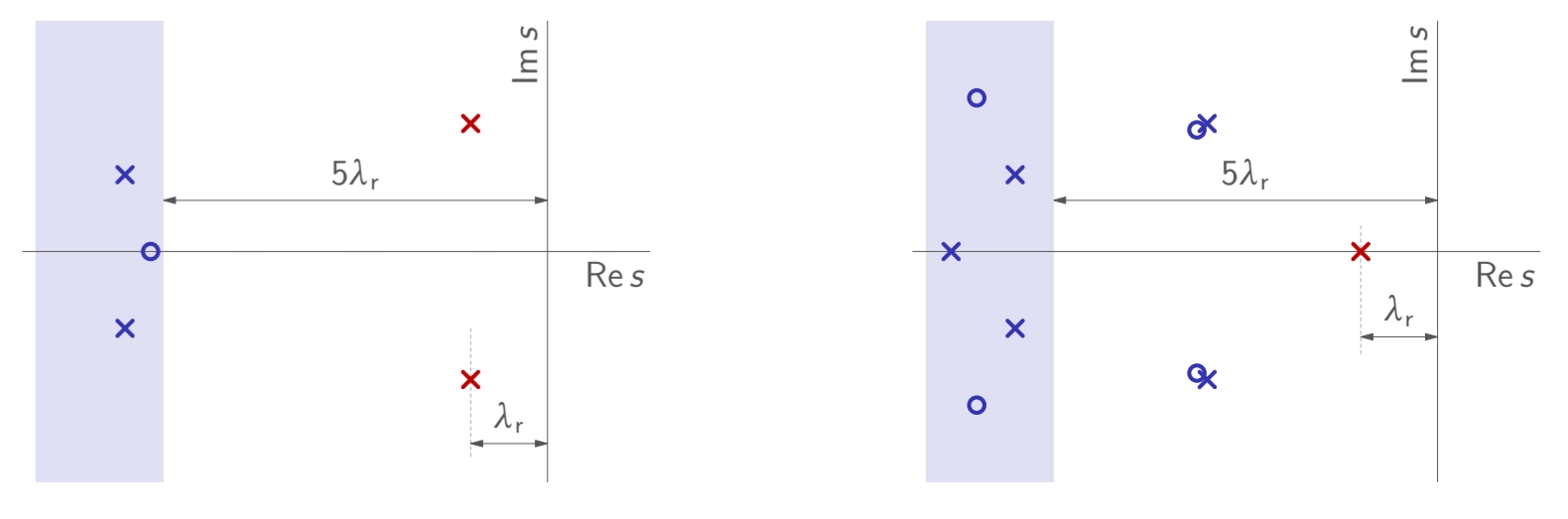
קטבים ואפסים (בכחול) שנחשבים לא דומיננטיים. קוטב מסומן ב-
, אפס מסומן ב- . (Leonid Mirkin’s Homepage, n.d.).
דוגמה:
לכל
, נגדיר: הקטבים הם
ויש אפס יחיד ב- . נשווה למערכת מסדר נמוך:
השוואה של התגובות מדרגה של המערכת ממעלה שלישית
ומערכת ממעלה ראשונה . (Leonid Mirkin’s Homepage, n.d.).
ניתוח תגובת תדירות
עוד דרך לאפיין מערכות היא בעזרת ניתוח תגובת תדירות (frequency-response analysis). נביט למשל בגרף בודה-הגבר (magnitude) של מערכת מסדר ראשון
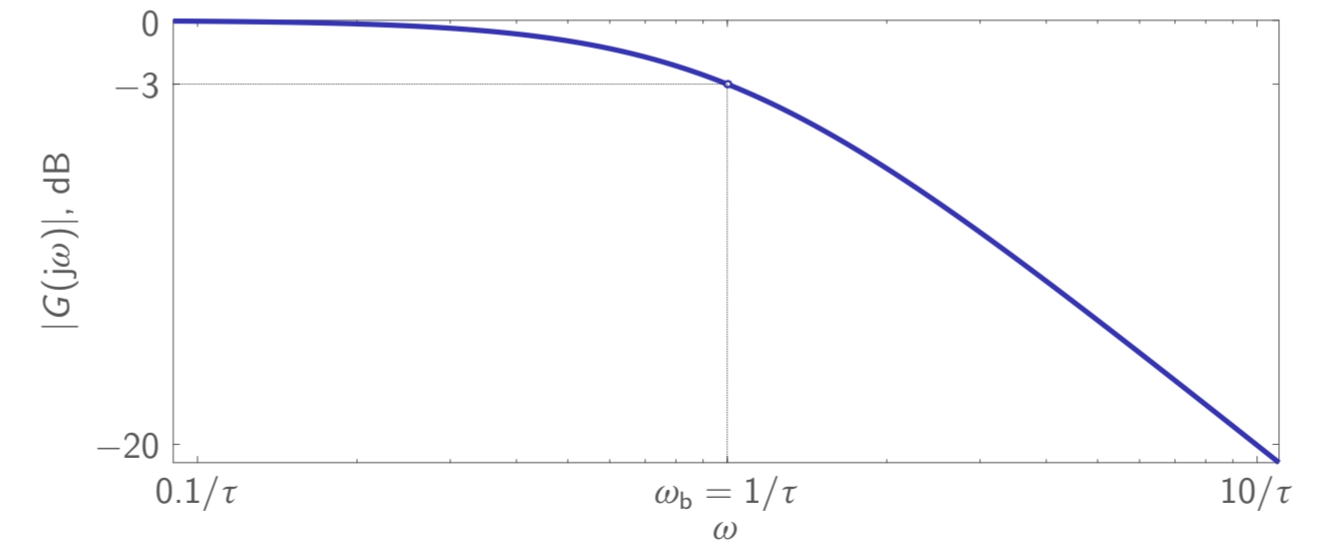
גרף בודה-הגבר (magnitude) של
. (Leonid Mirkin’s Homepage, n.d.).
נשים לב ש:
- ככל ש-
קטן, הרוחב-פס (bandwidth) מתרחב (תזכורת לפילטרים).
אם נביט בתגובת תדירות ומדרגה שלו:
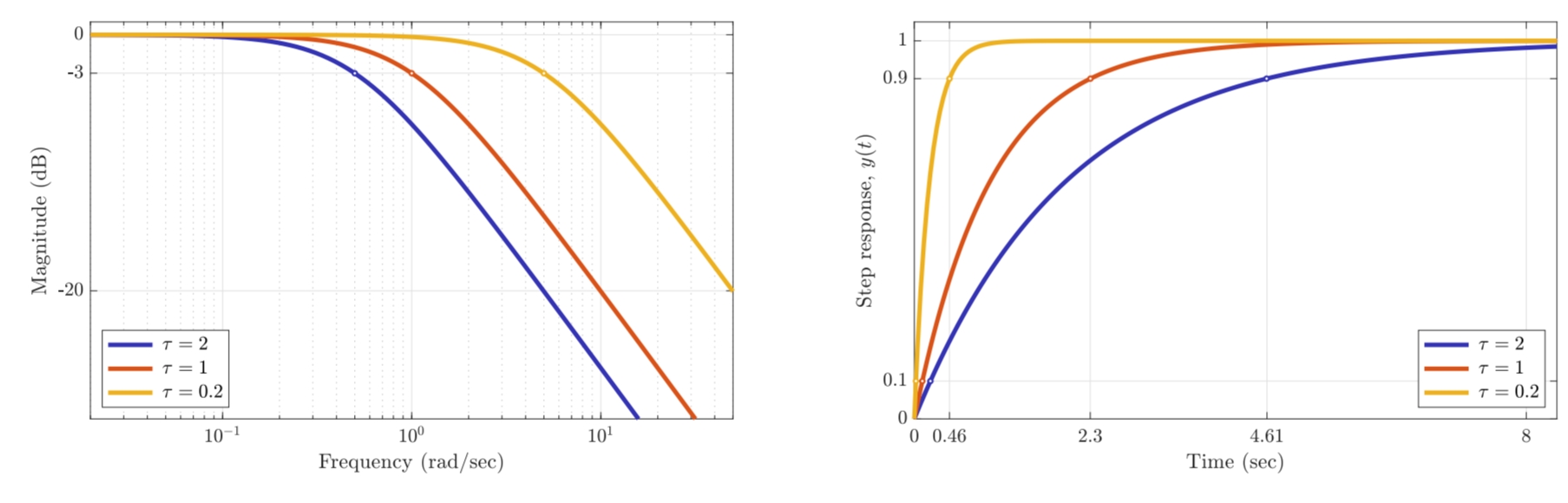
תגובת תדירות ומדרגה של
עבור שונים. (Leonid Mirkin’s Homepage, n.d.).
נסיק ש:
- עבור רוחב-פס רחב יותר אנו מקבלים זמן עלייה קצר יותר - תגובת מעבר מהירה יותר.
מבחינת מערכת מסדר שני:
הגרף בודה שלו:
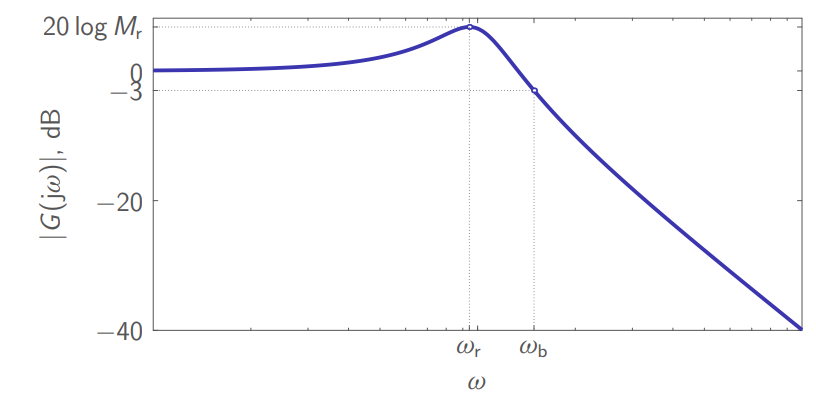
גרף בודה-הגבר (magnitude) של
. (Leonid Mirkin’s Homepage, n.d.).
נשים לב שהרוחב-פס
- גדל כאשר
גדל (והתגובת מדרגה הופכת להיות מהירה יותר). - גודל מעט כאשר
יורדת (והתגובת מדרגה הופכת להיות מהירה יותר).
פסגת התהודה (resonant peak): - גדל כאשר
קטנה (והתגובת מדרגה יותר רַעְדָנִית, shaky).
אם נביט בתגובת תדירות ומדרגה שלו עבור
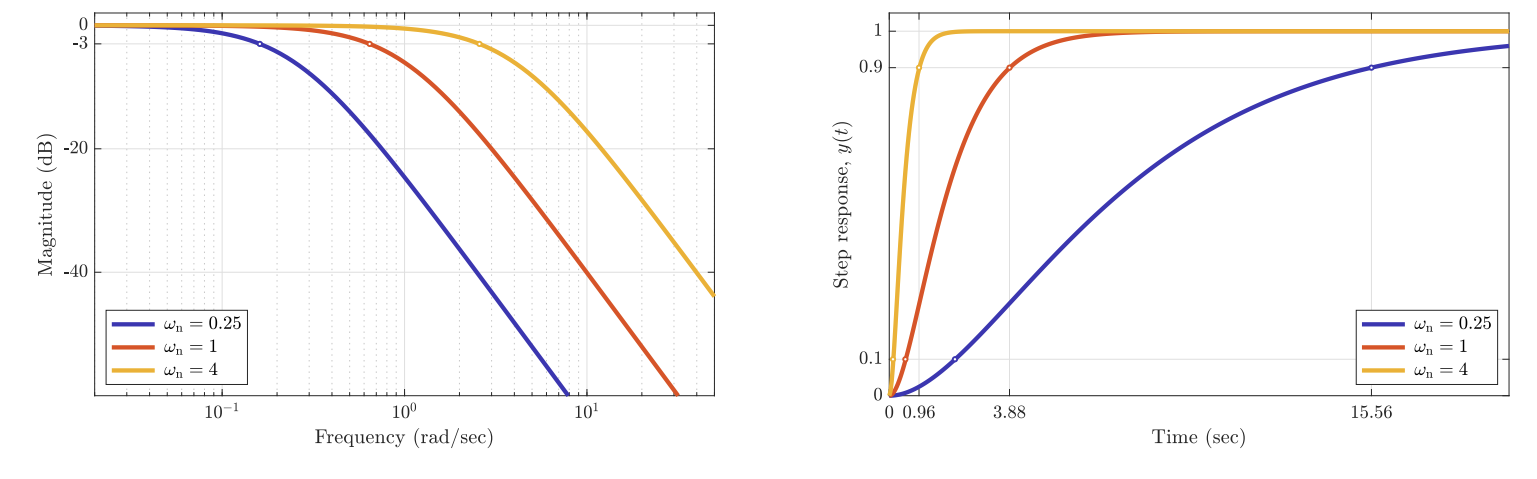
תגובת תדירות ומדרגה של
עבור ו- . (Leonid Mirkin’s Homepage, n.d.).
מה שמראה ש:
- רוחב-פס
רחב יותר מניב זמן עלייה קצר יותר (מעבר מהיר יותר).
עבור
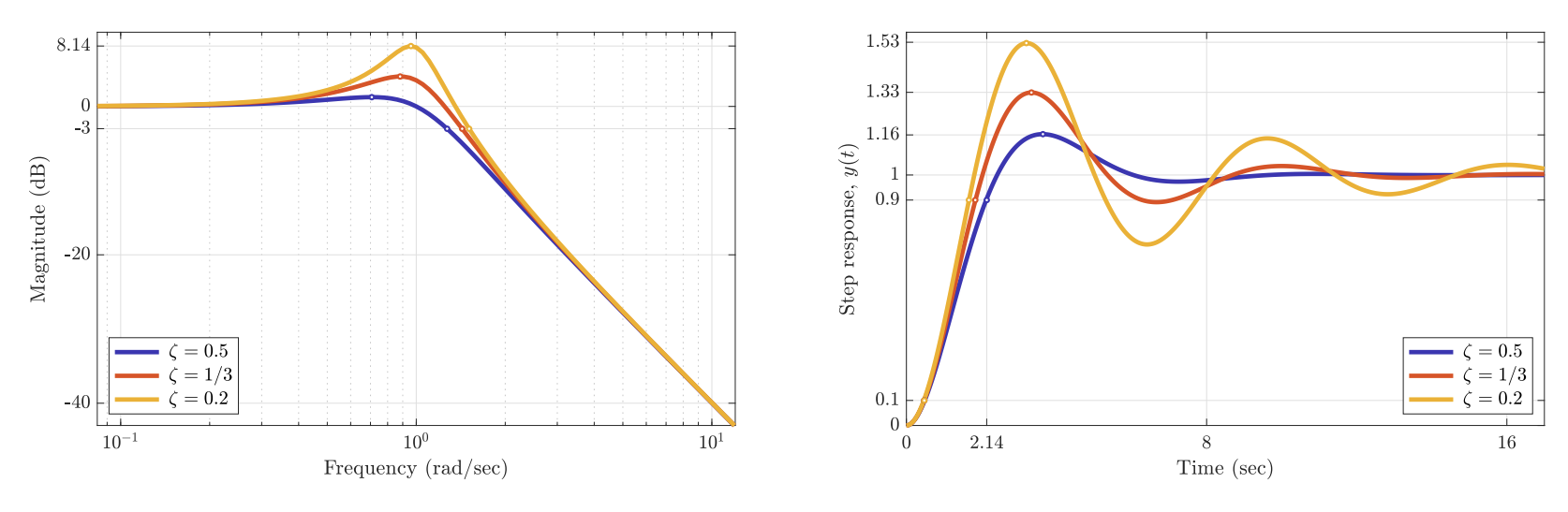
תגובת תדירות ומדרגה של
עבור ו- . (Leonid Mirkin’s Homepage, n.d.).
מה שמראה ש:
- תהודה
גדולה יותר גורמת לתגובת יתר גדולה יותר.
אחד מהיתרונות של ניתוח תגובת תדירות הוא שאת הכללי אצבע שעובדים עבור מערכות מסדר ראשון ושני ניתן גם להרחיב למערכות כלליות. למשל, אם:
ואז עם
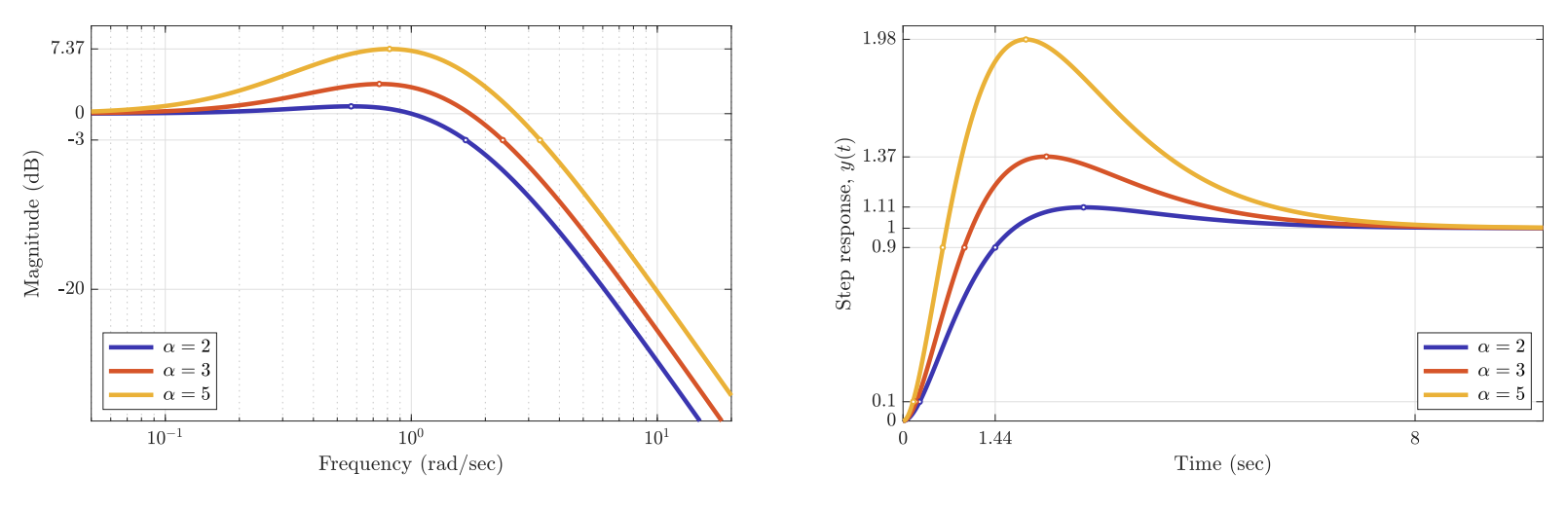
תגובת תדירות ומדרגה של
עבור ו- . (Leonid Mirkin’s Homepage, n.d.).
וגם כאן:
- רוחב-פס
רחב יותר מניב זמן עלייה קצר יותר (מעבר מהיר יותר). - תהודה
גדולה יותר גורמת לתגובת יתר גדולה יותר.
בכללי נוכל לומר ש:
טיפים:
- ככל ש-
גדול יותר, התגובות יתר וחסר יהיו גדולים יותר. - בדרך כלל:
- פסגות צרות יותר מעידות על תגובה תנודתית עם תדירויות הקרובות לתדירויות של הפסגה בדיאגרמת בודה-הגבר.
- פסגות רחבות יותר מעידות על תגובת יתר או חסר ללא תנודות.
- רוחב-פס
רחב יותר מניב זמן עלייה קצר יותר (מעבר מהיר יותר).
מודל ייחוס
בהינתן תהליך יציב

נרצה למצוא
- מייצב פנימית את המערכתץ
- מבטיח שגיאות אפסיות במצב מתמיד עבור אותות ייחוס מסויימים.
- מספק תגובת מעבר (transient) “טובה” (למשל, מספיק מהיר וחלק).
בעוד ייצוב המערכת הוא יחסית פשוט (צריך רק לדאוג שגם
נתחיל מלבטא את הבקר שאנו רוצים ב-
כאשר ה-
לכן, נרצה ש:
כדי שתהיה יציבות פנימית, צריך ש-
נסמן:
מיציבות פנימית, אנו צריכים ש-
נסיק כי לבקר
- כל אפס של
שנמצא ב- הוא גם אפס של .
בנוסף, הבקר הוא proper אמ”ם:
- עודף הקטבים של
הוא לפחות גדול כמו העודף קטבים של .
אם
חוץ מכך, נרצה גם שהמודל שלנו יהיה:
- עם מבנה low-pass:
- הרוחב-פס שנבחר כולל את התדירויות שאנו מעוניינים בהם ולא יותר (אין סיבה לבחור ברוחב פס רחב - קשה מדי ליישם, דורש די הרבה מאמץ מהבקר שלנו).
- ל-
יש לאות ייחוס מדרגה. - הקטבים ממוקמים באזורים “טובים” כדי שהמעברים יהיו חלקים.
- פשוט:
- לרוב נרצה
מסדר ראשון או שני. - אם לא ניתן להימנע ממערכות מסדר גבוה, אז נרצה שלפחות התגובה הדומיננטית תהיה מסדר ראשון או שני.
- אם חייבים להיות אפסים ב-RHP, נצמצם את הרוחב פס.
- לרוב נרצה
מאמץ בקרה
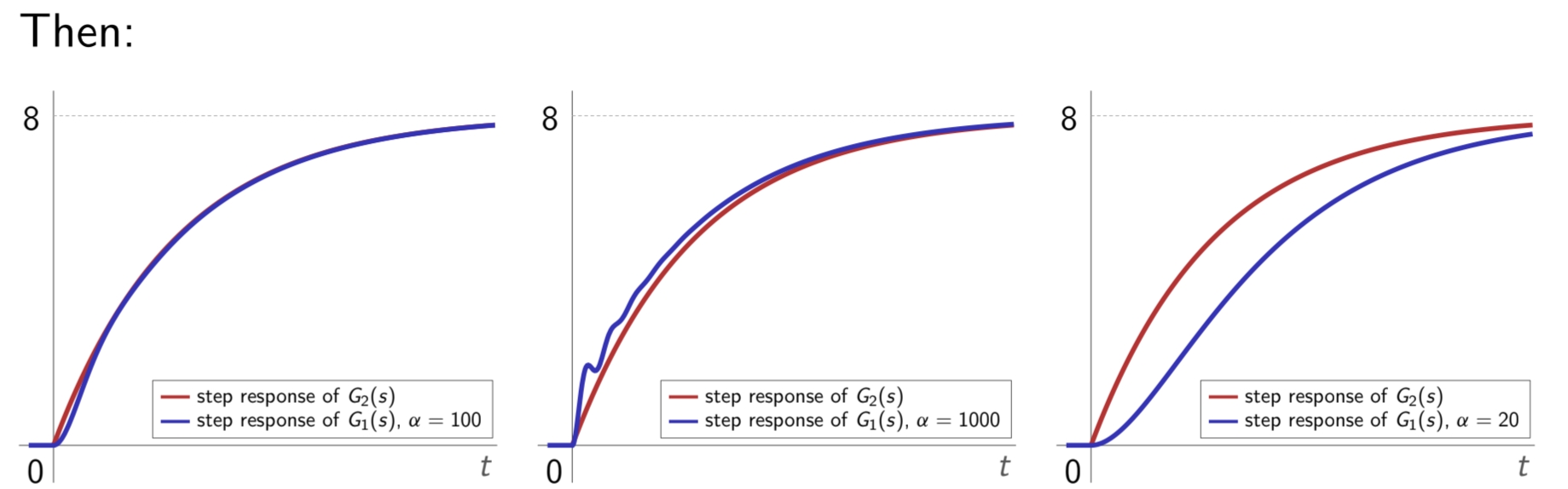
דוגמה:
בהינתן המעלית שלנו עם פונקציית תמסורת:
נוכל לבחור כליציב, שהפונקציית תמסורת שלו עם לפחות עודף קוטף אחד. לכן נוכל לבחור ו-נכוונן את קבוע הזמן שלו
כדי שיהיה לנו:
- תגובות מעבר מהירות מספיק
- רוחב פס רחב של תדירויות של
ש- יעקוב אחריהם (כלומר, כמה שיותר עבורם . נקבל בקר מהצורה:
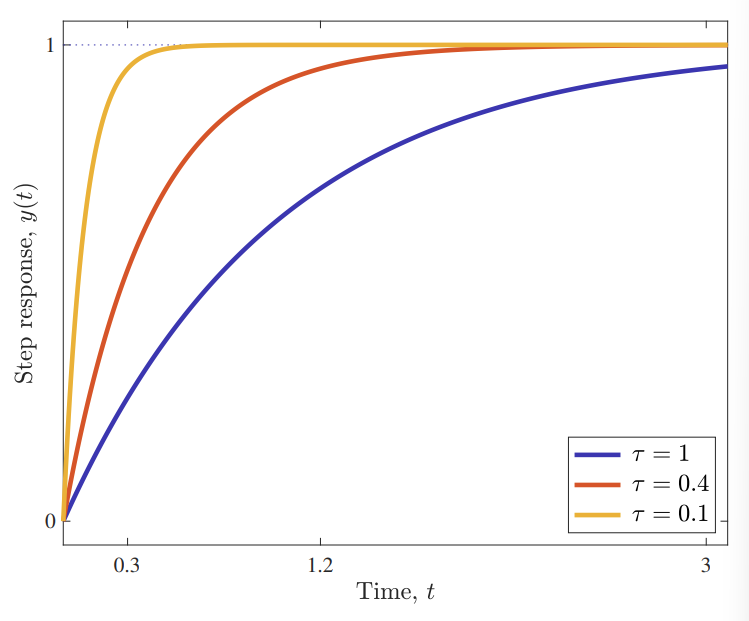
תגובת מדרגה של
. (Leonid Mirkin’s Homepage, n.d.). נדמה כי ניתן ליישם
לכל , ואם אנו רוצים תגובה מאוד מהירה, אנו רק צריכים לבחור קטנה מספיק.
הבעיה מתחילה כאשר נביט בתגובת מדרגה של הבקר:
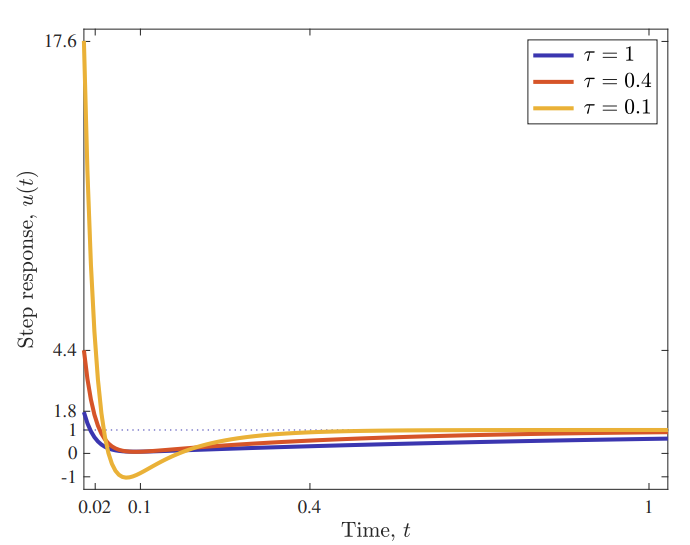
תגובת מדרגה של הבקר
. (Leonid Mirkin’s Homepage, n.d.). אנו יכולים לראות שעם ההאצה של
אנו דורשים יותר מהבקר שלנו - מהירות עצומה של . לתופעה זו אנו קוראים מאמץ בקרה, ונרצה להשאיר אותו כמה שיותר קטן. למשל, במקרה של המעלית המתוארת בדוגמה, קשה לנו מאוד לבנות מנוע שיוכל להגיע למהירויות זוויתיות עצומות כאלה. אנחנו גם לא נרצה לעשות זאת בדרך כלל, זה סתם יעיף את כל מי שבתוך המעלית לתקרה. נראה כי גם בתגובת תדירות יש לנו בעיה:
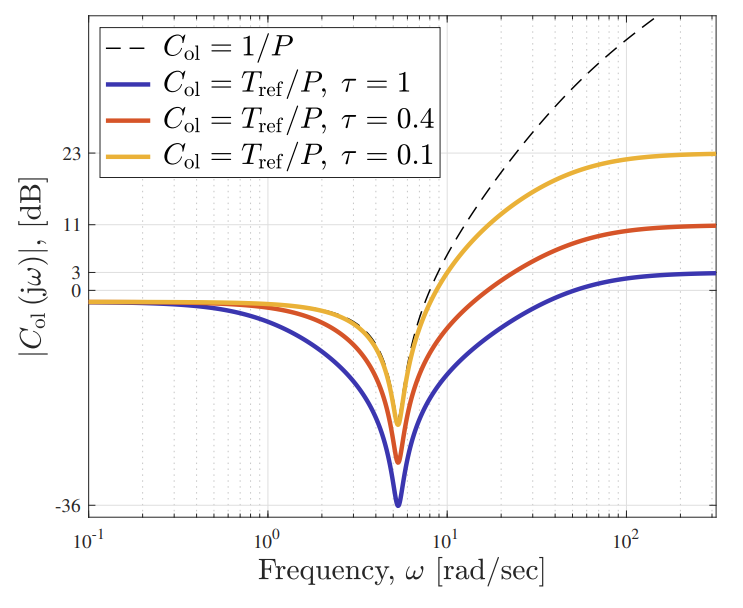
תגובת תדירות של
- דיאגרמת בודה-הגבר. (Leonid Mirkin’s Homepage, n.d.). ככל ש-
קטנה, השיאים של עולים, מה שגורם לשיאים יותר גבוהים ב- . הסיבה שאנו מקבלים שיאים כל כך גבוהים ב- נהיית יותר ברורה כאשר אנו ניזכר בהגדרה , וב- שדרשנו:
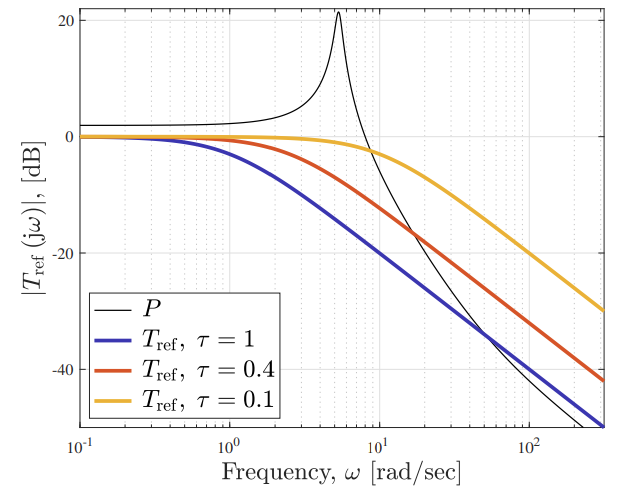
תגובת תדירות של
ו- -דיאגרמת בודה-הגבר. (Leonid Mirkin’s Homepage, n.d.). ניתן לראות שכאשר
אז גם , שזה נובע ישירות גם מההגדרה.
נרצה לדעת האם יש עוד תנאי שנוכל לדרוש על
ניתן לראות בדוגמה האחרונה (בגרף האחרון, יש גם גרף של
לכן, הדעיכה של
נסיק, שאולי, אם נדרוש על
דוגמה:
עם אותה המערכת מהדוגמה הקודמת, נבחר
מסדר שני כדי לקיים : למערכת זו רוחב פס מיוחד המקיים
, והיא נקראת פילטר Butterworth. במקרה זה: שהוא יציב לכל
, שהוא הדרגת חופש שלנו (מקודם היה לנו את , עכשיו זה ).
התגובות מדרגה:
תגובות מדרגה במערכת החדשה. (Leonid Mirkin’s Homepage, n.d.).
עדיין, האצה של
דורשת מאמץ בקרה יותר גבוה, ואם נביט בתגובת תדירות
תגובת תדירות של
- דיאגרמת בודה-הגבר. (Leonid Mirkin’s Homepage, n.d.). נראה שככל ש-
עולה, השיאים של גדלים.
אבל, כאשר נביט גם בתגובת תדירות של:
תגובת תדירות של
ו- -דיאגרמת בודה-הגבר. (Leonid Mirkin’s Homepage, n.d.). אנו רואים ש-
מתחילה לגדול מעל כאשר הרוחב פס של מתחיל לעבור את הרוחב פס של .
משתי הדוגמאות לעיל נסיק שככלל אצבע:
טיפ:
- כדאי לדרוש מודל ייחוס שהרוחב פס שלו לא עולה על הרוחב פס של התהליך, כי זה לרוב דורש מאמץ בקרה גדול לאמץ את התהליך להגיב מהר יותר מהמהירות תגובה הטבעית שלו (בהנחה ולשניהם יש מבנה low-pass).
תרגילים
תרגיל 1
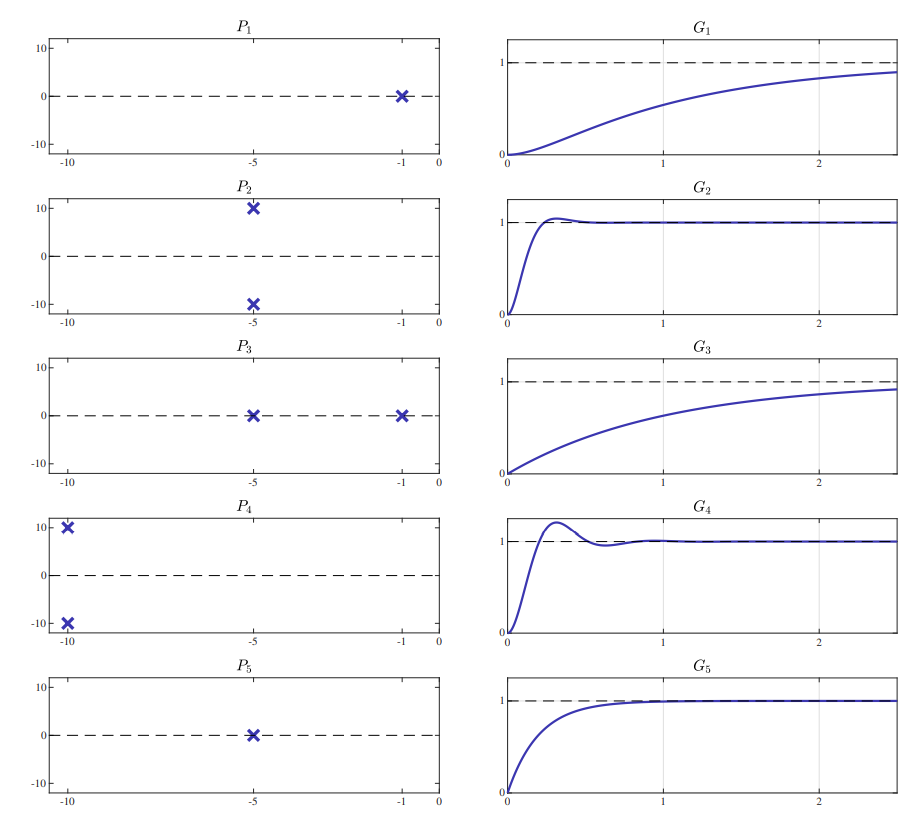
מפות קטבים-אפסים ותגובות מדרגה. (Leonid Mirkin’s Homepage, n.d.).
התאימו בין המפות קטבים-אפסים והתגובות מדרגה באיורים.
פתרון:
ניתן לראות מהמיקומי קטבים
עבור
מבחינת
מבחינת מערכות מסדר ראשון, יש לנו את
נשים לב גם שב-
תרגיל 2
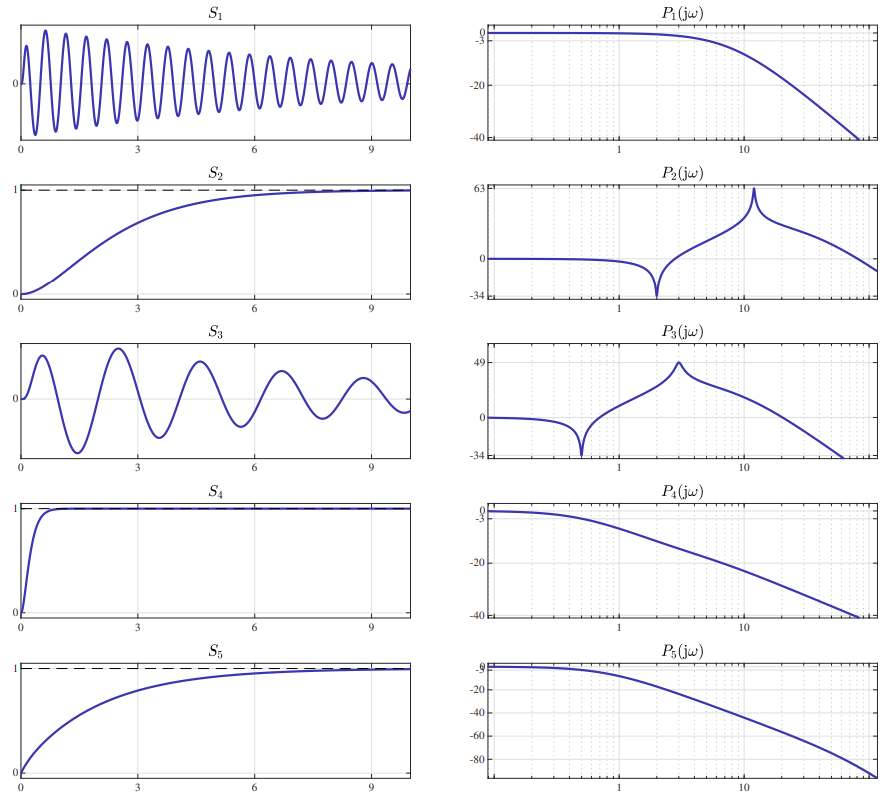
תגובות מדרגה ודיאגרמות בודה-הגבר. (Leonid Mirkin’s Homepage, n.d.).
התאימו בין התגובות מדרגה לדיאגרמות בודה.
פתרון:
אנו יודעים שלמערכות עם גרף בודה-הגברש יורד מונוטונית יש בדרך כלל תגובות מדרגה לא תונדות. בנוסף, ככל שרוחב הפס רחב יותר, התגובת מדרגה מהירה יותר. מבין הגרפי בודה, ה-
מבחינת
למערכות עם תהודות צרות יש בדרך כלל תגובות מדרגה תונדות, עם תדירויות הקרובות לתדירות התהודה. מבין
תרגיל 3
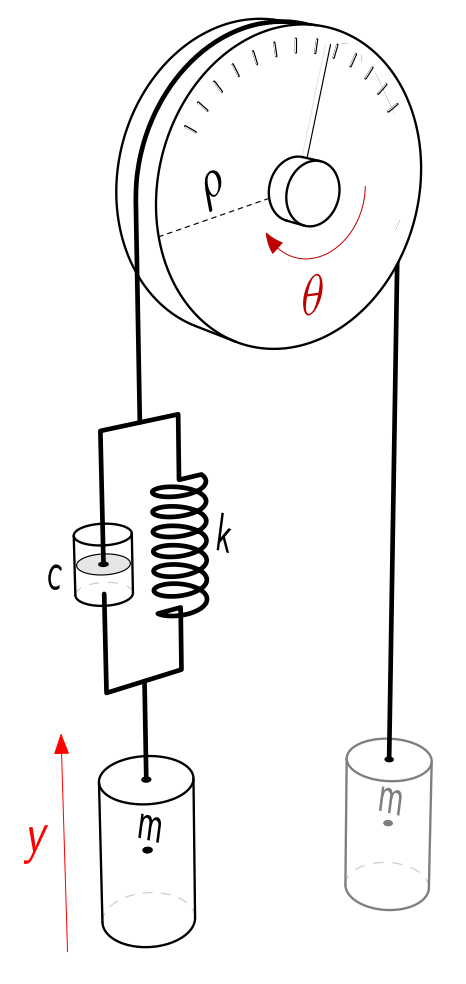
הביטו במערכת הבאה:
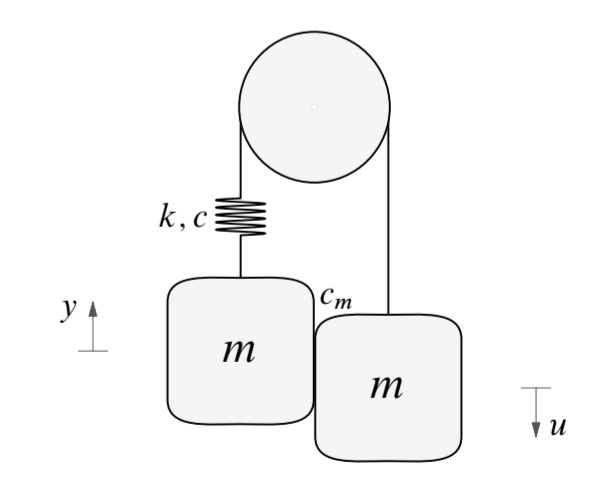
סכימת המערכת. (Leonid Mirkin’s Homepage, n.d.).
שתי מסות
סעיף א’
אם המסות לא נוגעות אחת בשנייה (כלומר, אין כוח חיכוך הפועל ביניהם, עם
מדלו את הבקר
תחת אלו תנאים על
פתרון:
עם התהליך הנתון והמערכת הרצויה
מערכת זו:
- היא proper אמ”ם
. - יציבה רק אם
, כי אז כל הקטבים שלו יהיו ב-LHP.
עבור
לפיכך המערכת יציבה פנימית אמ”ם
סעיף ב’
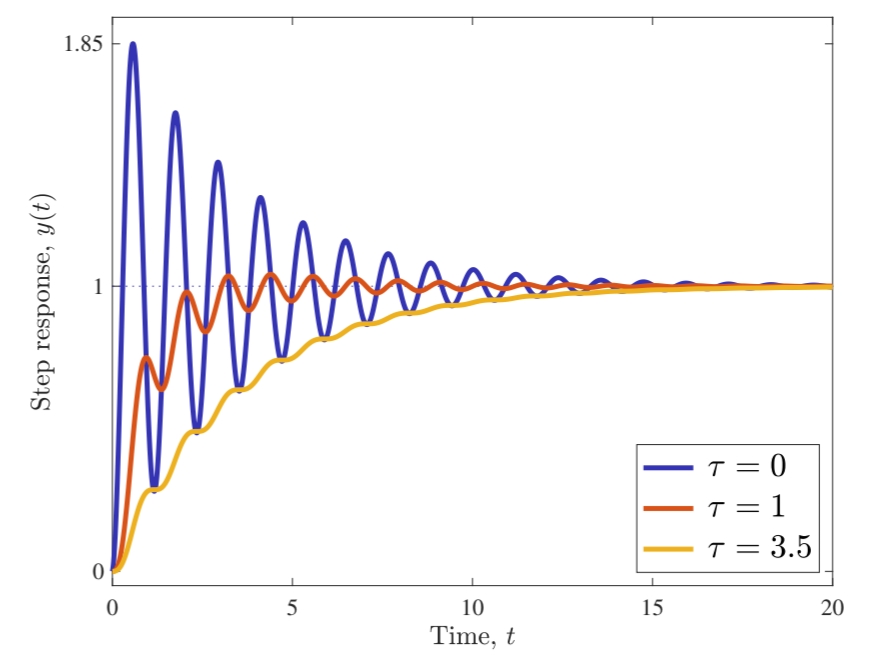
שרטטו את התגובות מדרגה של
פתרון:
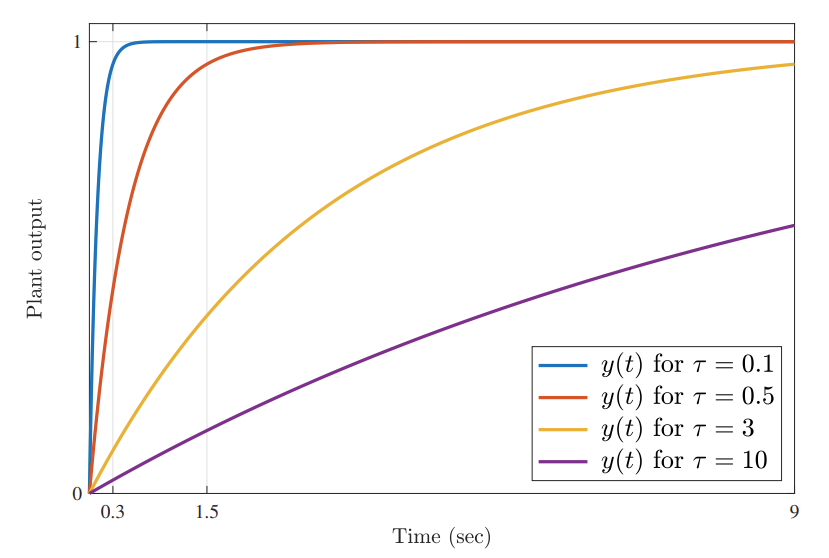
תגובת מדרגה של
. (Leonid Mirkin’s Homepage, n.d.).
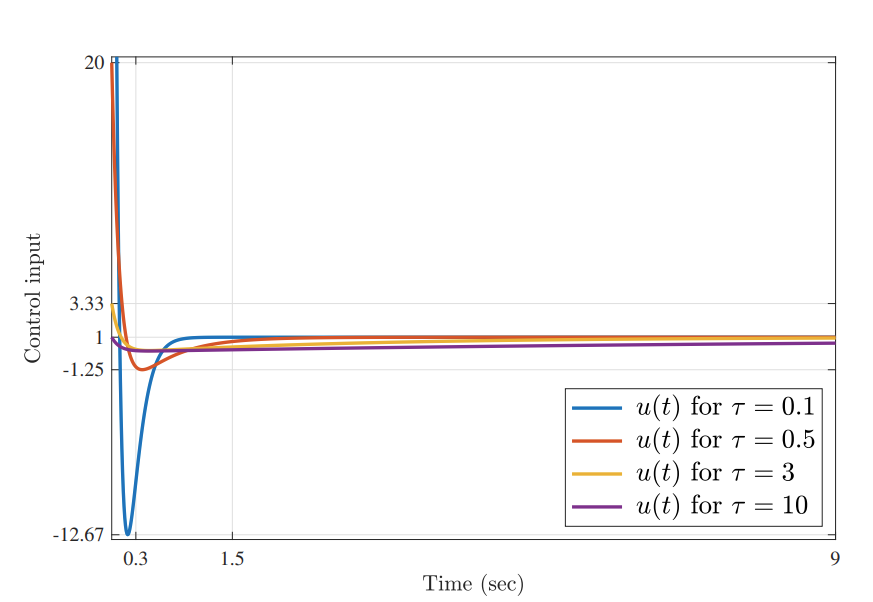
תגובת מדרגה של
. (Leonid Mirkin’s Homepage, n.d.).
ניתן לראות שכאשר קבוע הזמן של המערכת המבוקרת,
ניתן לראות זאת גם מהדיאגרמת בודה-הגבר של הבקר בגרף הבא:
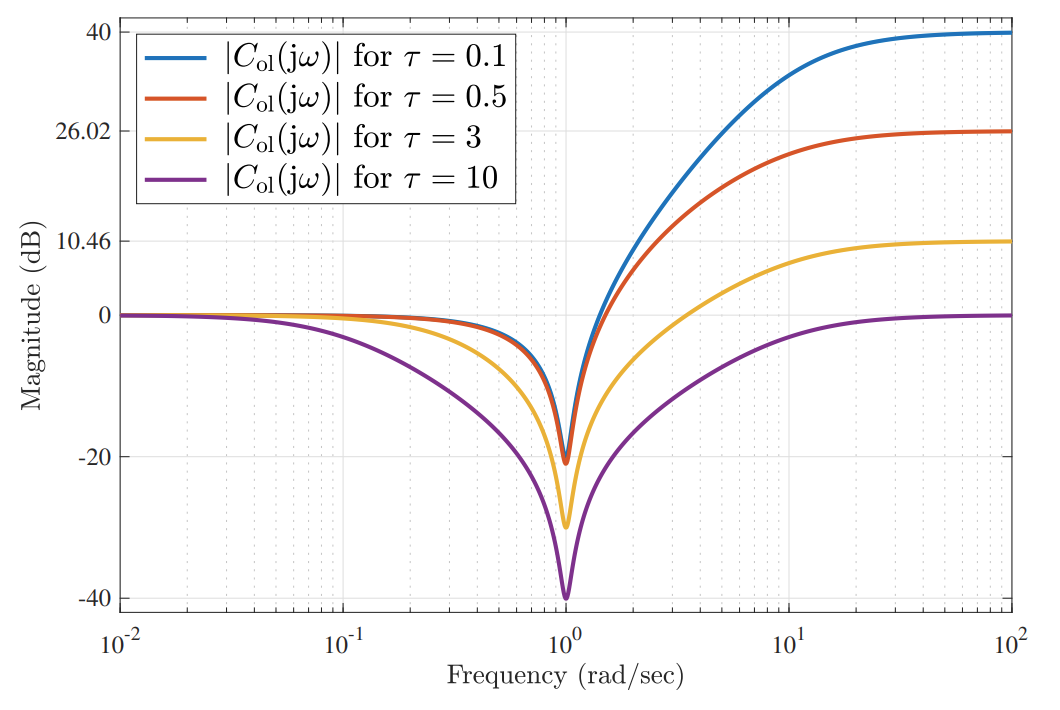
דיאגרמת עוצמה-בודה של
. (Leonid Mirkin’s Homepage, n.d.).
ההגבר הגדול בתדירויות הגבוהות אחראי לשיאים הגבוהים בהתחלה - הרגע בו המדרגה מופעלת. העלייה בעוצמה
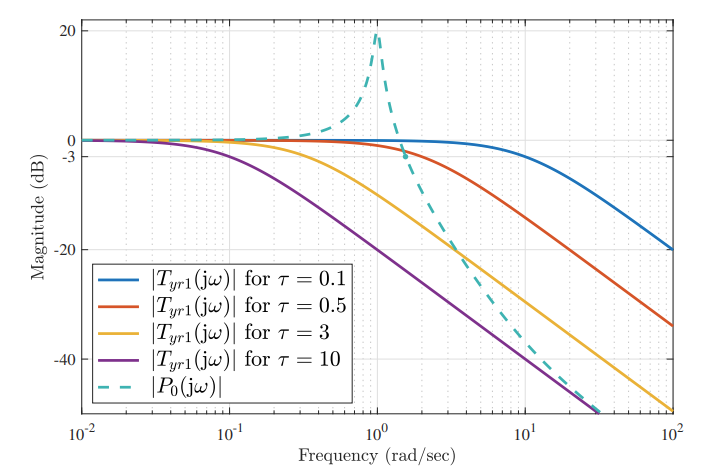
דיאגרמת עוצמה-בודה של
ו- . (Leonid Mirkin’s Homepage, n.d.).
אנו יכולים לראות שב-
סעיף ג’
נניח כעת שאנו צריכים שהשגיאת מצב מתמיד בין
עבור
פתרון:
כדי להבטיח שהמערכת המבוקרת היא
הפונקציית תמסורת הזו היא proper (מונה ממעלה רביעית, מכנה ממעלה רביעית), וכלל הקטבים שלו,
נדרוש כעת שהשגיאה היא אפסית במצב מתמיד לאות ייחוס עם תדירות
בגלל ההגבר של
כעת נעבור לתנאים על
נציב את
נציב
מ”השוואת מקדמים”:
נקבל את דיאגרמת הבודה:
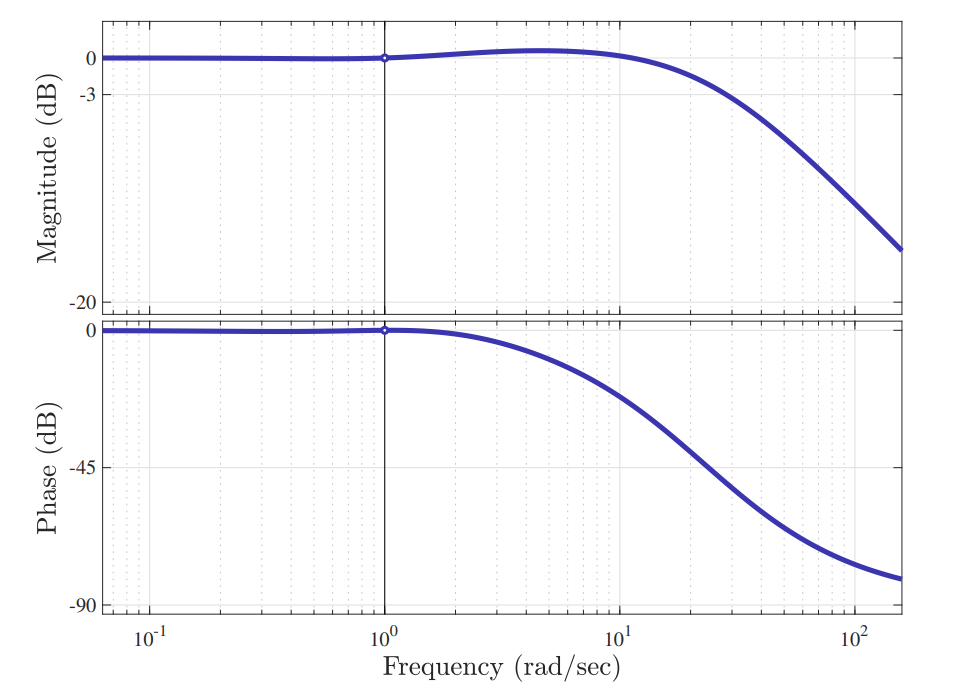
דיאגרמת בודה של
עבור . (Leonid Mirkin’s Homepage, n.d.).
ניתן לראות מהגרף לעיל שבאמת לבקר
סעיף ד’
כעת, הניחו שהמסות נוגעות אחת בשנייה, ויוצרים כוח חיכוך ביניהם עם מקדם
פתרון:
משוואת התנועה החדשה היא:
לכן פונקציית התמסורת של המערכת היא:
כיוון ש-
סעיף ה’
שרטטו סכמתית את התגובת מדרגה של המערכת.
פתרון:
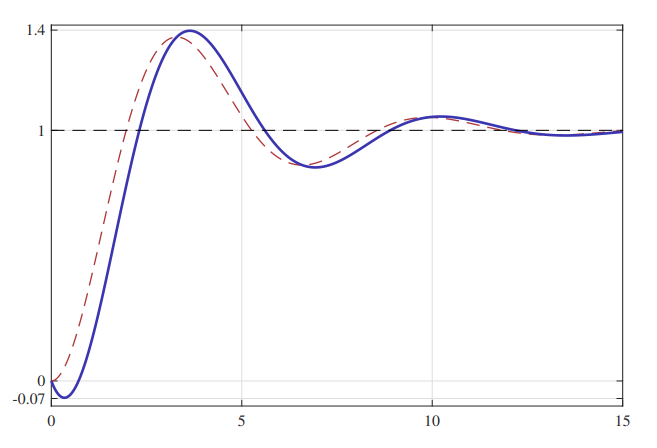
תגובת מדרגה של
(בכחול) כאשר . הקו האדום מייצג תגובת מדרגה של מערכת מסדר שני תת-מרוסנת עם שני קטבים שמאליים, וללא אפסים. (Leonid Mirkin’s Homepage, n.d.).
תרגיל 4
הביטו בבקר בחוג פתוח הבא:

כאשר התהליך:
סעיף א’
האם תהליך זה ניתן לבקרה ע”י השימוש במודל ייחוס? אם כן, מהם התנאים למודל ייחוס זה כדי להבטיח את היציבות הפנימית של מערכת הבקרה?
פתרון:
לפי מודל ייחוס, אנו רוצים ש:
- התהליך
יציב BIBO - מתקיים כי הוא proper וכל הקטבים שלו ב-OLHP. - כל אפס ימני של
הוא גם יהיה אפס ימני של - נוכל לקיים, כי אין אפסים ימניים ל- . - עודף הקטבים של המודל ייחוס יהיה לפחות כמו עודף הקטבים של
- נוכל לקיים.
סעיף ב’
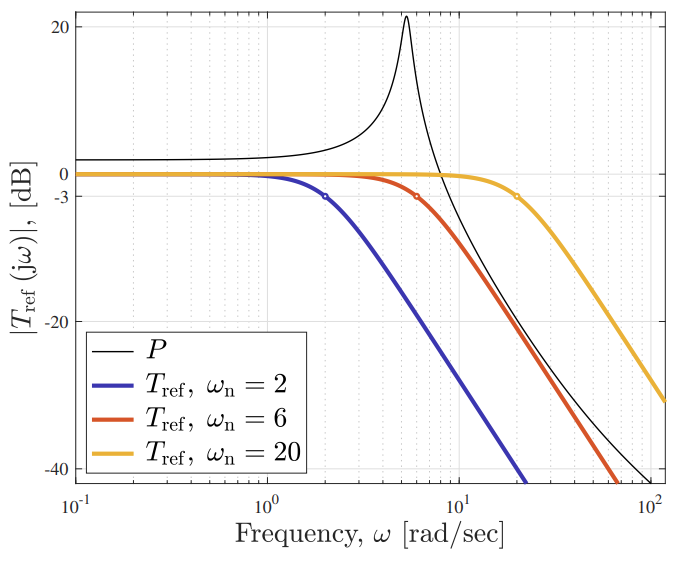
הביטו במודל ייחוס מסדר שני
(לפונקציית תמסורת זו רוחב פס
פתרון:
נחשב את
הבקר הוא proper וכל קטביו נמצאים ב-OLHP. בנוסף, אין צמצומים לא יציבים ולכן הבקר תקין והמערכת יציבה פנימית.
סעיף ג’
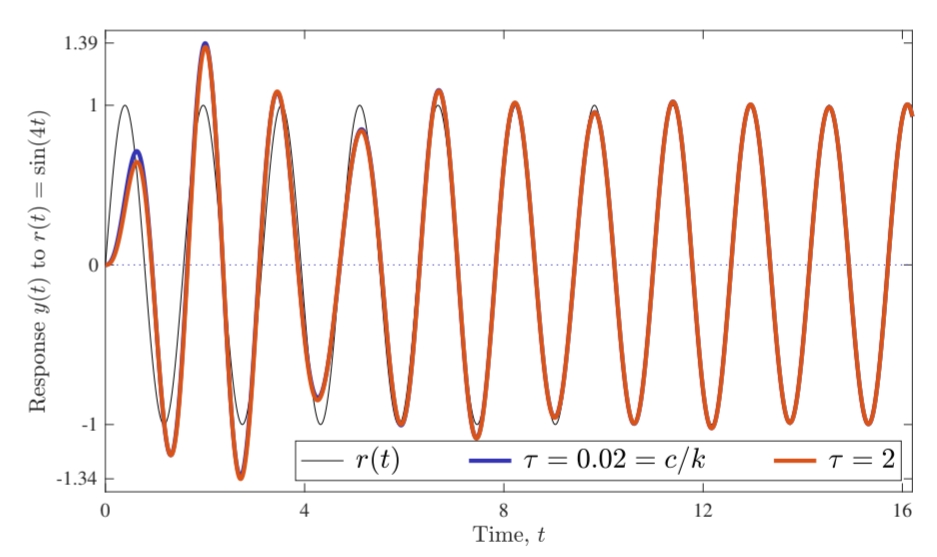
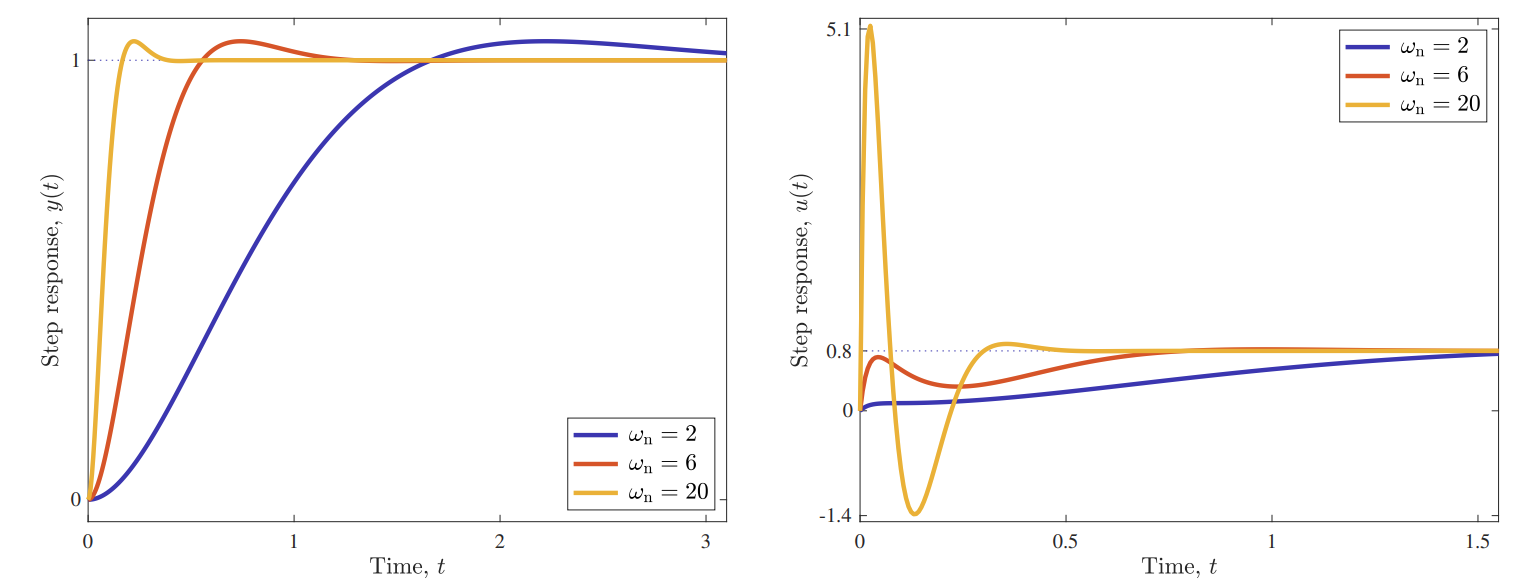
שרטטו את התגובות מדרגה של
פתרון:
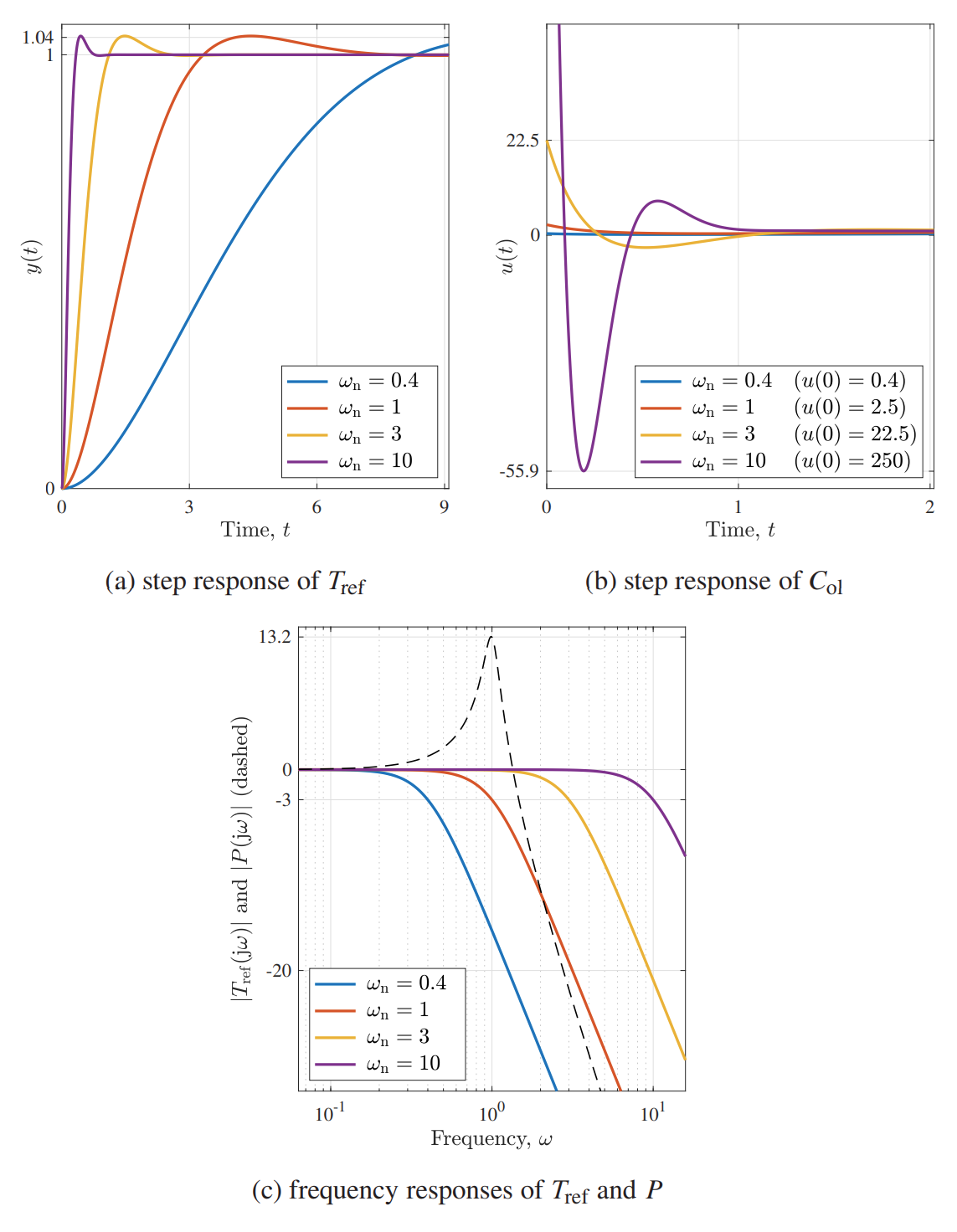
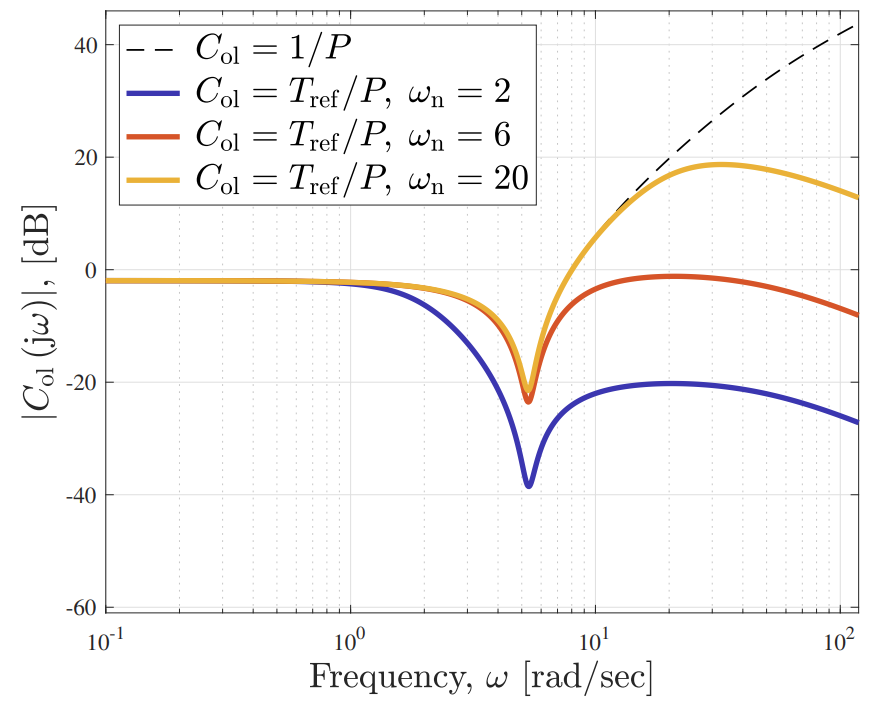
תגובות תדירות של
ו- . הקו המקווקו ב-(c) הוא התהליך עצמו. הסיבה שיש שם Resonance זה מהיחס ריסון קטן מ- במכנה של .