HTF1_HW002 תרגיל בית 2

	סטודנט א’
שם	עידו פנג בנטוב
ת”ז	322869140
דואר אלקטרוני	ido.fang@campus.technion.ac.il

שאלה 1

סכמת הבעיה.

סעיף א’

מסימטריית הבעיה, נוכל פשוט למדל חצי מהמערכת, והחצי השני יהיה זהה לה. כלומר, נקבל משהו מהצורה:

מעגל תרמי שקול לבעיה.

כאשר תקף רק לחצי מהמוט. חשוב גם לציין שאין מעבר חום חד ממדי מהקורה לקיר, אבל אנו יכולים למדל את מעבר חום זה כנגד אם אנו נשתמש במקדם צורה.

סעיף ב’

לפי טבלה 4.1, מקרה 10, מקדם הצורה הרלוונטי למקרה שלנו הוא . לכן ההתנגדות התרמית:

נתון כי גדול פי משטח חתך המוט, שהוא שטח חתך מעגלי בקוטר . כלומר:

נציב בחזרה ב- עם שאר הפרמטרים הידועים:

סעיף ג’

לפונקציית השטח הנתונה

יש ערך ב- שאנו יודעים (שטח החתך של המוט):

ולכן:

נציב פרמטרים:

נניח שבקורה יש התנגדות תרמית חד-ממדית. כיוון ששטח הנגד התרמי משתנה לאורך הקורה, נחשב את ההתנגדות באופן דיפרנציאלי. לפי התנגדות תרמית להולכה:

נציב פרמטרים ונקבל:

סעיף ד’

מהאופן שבו נצילות צלע מוגדרת, נוכל להשיג ביטוי עבור ההתנגדות שלה:

מטבלה 3.5 הנצילות צלע של מוט היא

כאשר , והתיקון אורך לצלע לא רלוונטי כי יש בידוד בקצה, אבל כן נשים לב לחשב עבור רק חצי מהמוט כי כך מידלנו את המעגל התרמי. כלומר, כאשר הוא אורך המוט. בנוסף, במקרה שלנו .
נחשב בנפרד את :

נציב ב-:

נציב בהתנגדות:

סעיף ה’

מקיר אחד, ההתנגדות הכללית היא:

לכן המעבר חום:

נקבל:

כעת בעזרת ההתנגדות בקיר נוכל לחלץ את (המעבר חום דרך הקיר זהה למעבר חום מהקיר לסביבה במצב מתמיד):

נקבל:

סעיף ו’

כדי למצוא את הטמפרטורה במרכז המוט נמצא את פילוג הטמפרטורות במוט. כיוון שהבעיה סימטרית נוכל להתייחס למרכז המוט כקצה אדיאבטי - אין מעבר חום מצד אחד לאחר. לפי טבלה 3.4, עבור קצה אדיאבטי:

כאשר הוא הפרש הטמפרטורות בקצה המוט .

בפרט, עבור (מרכז המוט), המשוואה לעיל:

נחשב את באותו אופן כמו סעיף קודם:

נציב נתונים ונקבל:

נציב בביטוי ל-:

שאלה 2

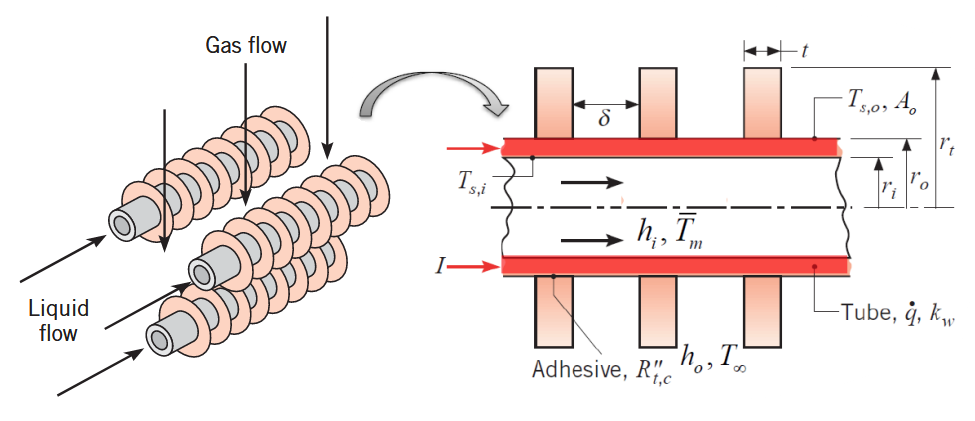
סכמת הבעיה.

סעיף א’

לפי נצילות כוללת, כאשר יש התנגדות מגע:

כאשר אצלנו יש צלעות. כל אחת מצלעות אלה עם פרופיל מרובע, כך שלפי טבלה 3.5, אנו תאורטית יכולים למצוא אותה מהשורה לצלע טבעתית עם פרופיל מרובע. הבעיה בנוסחה זו שהיא מאוד מסובכת, ואפשר במקום זאת להיעזר בגרף לנצילות צלעות טבעתיות. כדי להשתמש בגרף זה, נמצא את ערך הציר האופקי, כאשר נשים לב שבמקרה שלנו עם תיקון לאורך :

נציב נתונים ונקבל:

בגרף, זה מתאים לערך נצילות (כאשר ):

נחשב את :

גדלים נוספים:

נציב הכל ב-:

סעיף ב’

המקדם מעבר חום מוגדר באופן הבא:

במקרה שלנו:

נשים לב שבצד ימין, הביטוי הימני הוא ההופכי של התנגדות התרמית משפת הצינור אל הסביבה, שזה התנגדות המערכת צלעות - . לכן:

את ההתנגדות אנו גם יודעים לחשב מהנצילות של המערך צלעות:

ולכן:

נציב נתונים ופרמטרים ידועים:

סעיף ג’

נתחיל ממשוואת ההולכה:

אנו מניחים מצב מתמיד:

בקואורדינטות פולאריות:

תנאי השפה הם הסעה בדופן הפנימית, והסעה מורכבת בדופן החיצונית שנפשטה ע”י המקדם מעבר חום שמצאנו (המקדם מעבר חום מוגדר באותו אופן כמו חוק הקירור של ניוטון, כך שאפשר להשתמש בו בצורה דומה):

סעיף ד’

אם אנו מתייחסים לצינור כאל קיר שטוח, משוואת החום מהסעיף הקודם חוזרת להיות בקואורדינטות קרטזיות:

ראינו עבור [[HTF1_002 הולכה חד-ממדית במצב מתמיד#הולכה עם ייצור חום פנימי#לוח פשוט|הולכה חד-ממדית בקיר פשוט עם ייצור חום]] שהפתרון עבור תנאי שפה של טמפרטורות מוגדרות בקצה הוא:

בפתרון זה גם בחרנו מערכת צירים באמצע הלוח, כך שתנאי השפה שלנו ב- עם .

בנוסף, אנו לא יודעים מה הטמפרטורות על משטחי הלוח, אבל אנחנו כן יודעים מחוק הקירור של ניוטון והגדרת מקדם החום ש:

במצב מתמיד ה--ים קבועים. בנוסף נתון שמקדם ההסעה ו- (ולכן גם שפרופורציונלי ל-) גדולים מאוד. נסיק שבקירוב:

מה שאומר:

נציב הכל בפילוג הטמפרטורה:

נמצא את המקסימום - נגזור:

ונשווה לאפס:

נציב בחזרה בפילוג טמפרטורה כדי לקבל ביטוי ל-:

נעביר אגף:

נמצא את ה--ים המתאימים:

ה- בכלל לא בטווח של הלוח ( ולכן נלך עם הפתרון השני:

הסיבה שה- שלנו יצא שונה הוא נטו בגלל הבחירת מערכת צירים.

שאלה 3

סכימת הבעיה.

סעיף א’

המעגל התרמי השקול הוא פשוט שני נגדים, אחד הסעה ואחד הולכה, המחוברים בטור:

מהגדרת ההתנגדות התרמית, המעבר חום:

נציב נתונים ():

אותו החום גם הגיע לצד הכרטיס דרך ההולכה:

מתקיים , ולכן הטמפרטורה:

זוהי תוצאה הגיונית - ההולכה בכרטיס מאוד גבוהה כך שבמצב מתמיד הטמפרטורה בצד אחד כמעט זהה לטמפרטורה בצד השני.

סעיף ב’

עם הנתונים החדשים נישאר עם שלושה מרכיבים במעגל התרמי:\

• התנגדות להולכה בתוך הכרטיס .
• התנגדות להולכה של הדבק .
• התנגדות להולכה של האלומיניום .
• התנגדות מערך הצלעות .

האלומיניום והדבק רק בעובי של , אז ההשפעה שלהם גם כן תהיה נמוכה על הפרש הטמפרטורות מצד אחד של הלוח לסביבה, אז נזניח אותם. נישאר עם התנגדות הכרטיס והתנגדות מערך הצלעות:

כאשר:

ואז:

מטבלה 3.5, עבור צלעות עגולות:

נחשב את ( הוא אורך הצלע):

נציב בביטוי ל-

נשים לב גם ש:

נציב ב-:

ולכן ההתנגדות:

מכל ההזנחות שלנו, המעבר חום מהכרטיס לסביבה כעת ניתן לידי ביטוי כ:

נציב נתונים ונקבל:

באותו אופן כמו סעיף קודם, נחשב את :

ההבדלים בתוצאות נובעים מההזנחות.