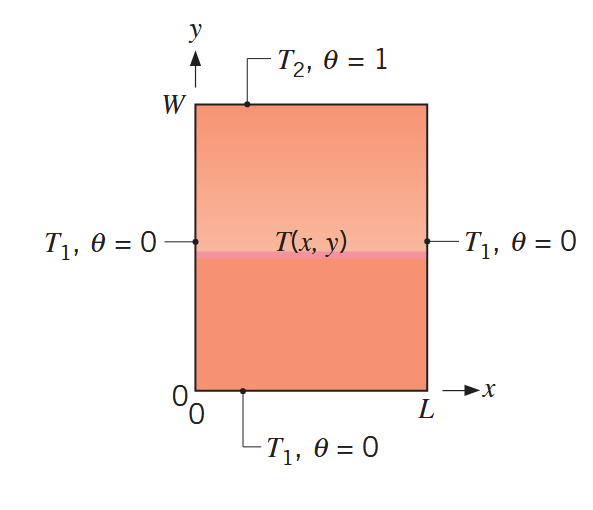מבוא
נביט במוצק ארוך דו-ממדי, בו יש מעבר חום דו-ממדי, עם שתי צלעות מבודדות ושתי צלעות עם טמפרטורות שונות קבועות כך ש-
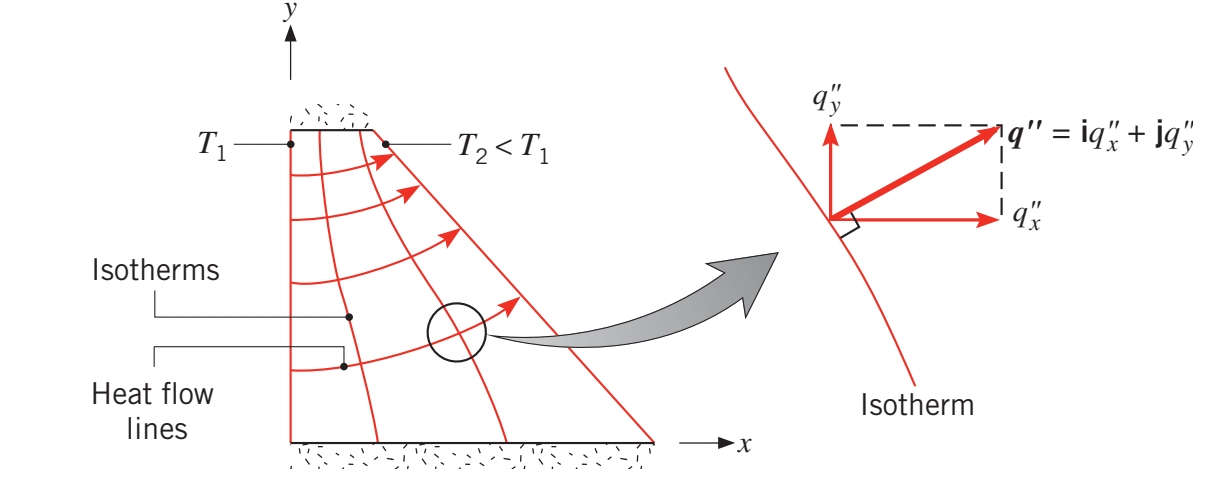
הולכה דו-ממדית. (Bergman & Lavine, 2017).
לפי חוק פורייה, השטף חום במוצק הוא וקטור שבכל מקום מקביל לקווים של טמפרטורות קבועות (איזותרמות). הכיוונים של וקטור שטף החום מתוארים ע”י ה-heat flow lines באיור, והוקטור עצמו הוא סכום של שטף החום בכיוונים
מאחר והקווי מעבר חום, מהגדרה, בכיוון של מעבר החום, שום חום לא יכול להיות מולך בניצב לקו חום ולכן לפעמים קוראים להם אדיאבטות (adiabats).
להולכת חום דו-מדדית, ללא יצירת חום, במצב מתמיד, והולכת חום קבועה, משוואת ההולכה היא:
שזה בדיוק הסוגי משוואות שעסקנו בהם במד”ח - משוואות לפלס, שאנו פותרים לפי שיטת הפרדת משתנים.
דוגמה: הולכה בלוח מלבני
שלושה צלעות של לוח מלבני נשמרים בטמפרטורה קבועה
, כאשר הצד הרביעי נשמר בטמפרטורה קבועה .
הולכה דו-מדדית בלוח מלבני דק. (Bergman & Lavine, 2017).
נזניח מעבר חום מהפאות של הלוח, גרדיאנט טמפרטורה ניצב למישור
( ). אנו מעוניינים בפילוג טמפרטורה, אבל כדי לפשט את הפתרון נציג את הטרנספורמציה
כך שמשוואת ההולכה שלנו היא כעת:
כיוון שהמשוואה מסדר שני, נדרוש שני תנאי שפה לכל קואורדינטה, שהם:
כך ששלושה מתוך ארבעת התנאי שפה הם הומוגניים.
לפי שיטת הפרדת המשתנים, נניח שהפתרון מהצורה:נציב בחזרה במד”ח, נפתור את הבעית שטורם-ליוביל, נציב תנאי שפה ע”י פירוקם לטור פורייה, ונקבל בסוף ש:
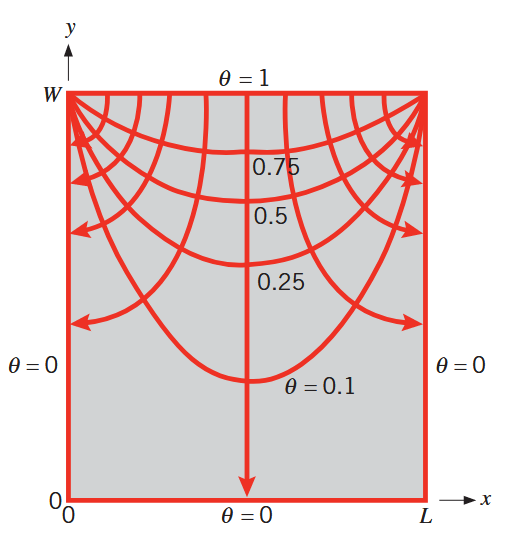
נוכל לשרטט את הפתרון:
איזותרמות ואדיאבטות להולכה דו-ממדית בלוח מלבני. (Bergman & Lavine, 2017).
שיטת נוספות לפתירת בעיה זו היא פתרון גרפי ופתרון נומרי. נסביר בקצרה על השיטה הגרפית.
שיטה גרפית לפתרון משוואת חום דו-ממדית
למרות ששיטה זו הוחלפה ע”י שיטות פתרון נומריות, היא עדיין שיטה טובה לקבלת שיעור ראשוני לפילוג טמפרטורה ופיתוח אינטואיציה אליו.
נביט בתעלה ריבועית שהמשטחים הפנימיים והחיצוניים שלה נשמרים קבועים בטמפרטורות
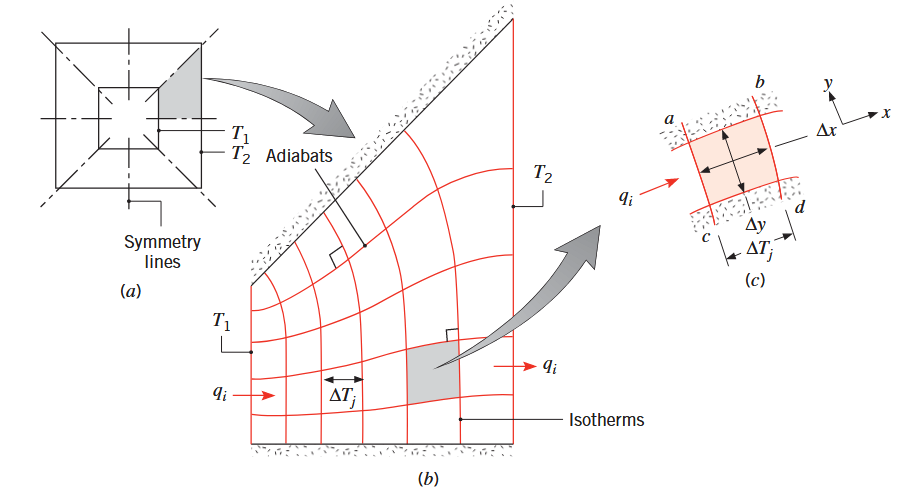
הולכה דו-ממדית בתעלה ריבועית עם אורך
. (a) מישור סימטריה. (b) גרף שטף. (c) ריבוע עֲקֻמִּי (curvilinear) טיפוסי. (Bergman & Lavine, 2017).
- בשלב הראשון נחפש קווי סימטריה גאומטריים וגם תרמיים. בשרטוט, ב-(a), אלו הם הקווים המסומנים. קווי סימטריה אלו יהיו אדיאבטות - לא יכול להיות מעבר חום בכיוון הניצב לקווים אלו.
- אדיאבטות ואיזותרמות תמיד ישורטטו בניצב אחד לשני.
- אדיאבטה שחוצה פינה איזותרמית תמיד יוצרת חוצה זווית לפינה.
- אדיאבטה ניצבת למשטחים איזותרמיים.
- איזותרמה ניצבת למשטחים אדיאבטיים.
- נרצה שייווצרו בשרטוט ריבועים עקומיים (curvilinear) - כלומר, שאורך כל צלע תהיה בערך שווה, או לפחות שהסכום של כל שתי צלעות נגדיות יהיה בערך שווה. דרך אחרת להגדיר ריבועים אלו היא לדרוש שהזווית בין האלכסונים תהיה בערך
.
מקדם צורה
ככלל, מציאת פתרונות אנליטיים למשוואה החום הדו-ממדית או תלת-ממדית היא תהליך ארוך, וברוב המקרים, בלתי אפשרי. לכן, פותחה שיטה לקיצור התהליך - במקרים רבים, נוכל להשתמש בפתרונות קיימים למשוואות חום, ע”י לקיחת בחשבון את מקדם הצורה
הגדרה: מקדם צורה
מקדם הצורה מוגדר כך ש:
כאשר
הוא הפרש הטמפרטורה בין הגבולות. נסיק שההתנגדות התרמית להולכה הדו-ממדית ניתנת לביטוי כ:
בטבלה 4.1 מוצגים מקדמי הצורה של בעיות חום נפוצות.
דוגמה: הולכה בחוט חשמלי
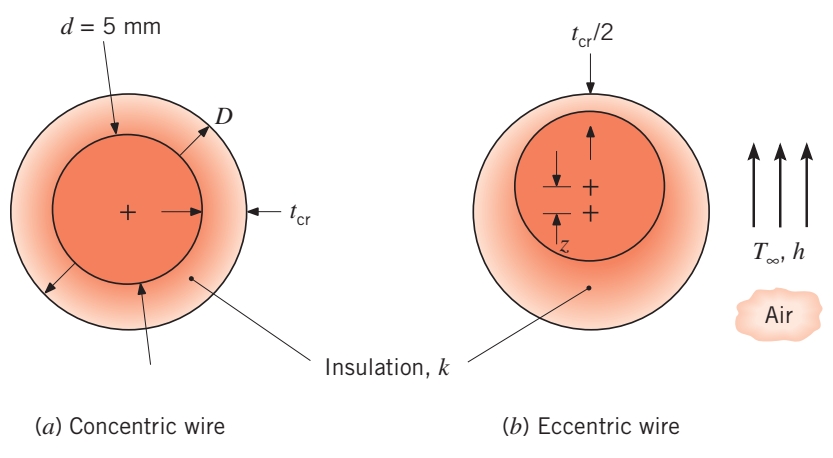
חוט חשמלי בקוטר
מצופה בחומר מבודד ונמצא בסביבה בה . למרות שתוכנן בידוד אופטימאלי התברר שבתהליך הייצור החוט לא נמצא במרכז הבידוד ושהוא זז עד מעובי הבידוד.
מצא בכמה השתנתה ההתנגדות התרמית ביחס לתכנון.פתרון:
מהדוגמה על בידוד צינורות, הרדיוס הקריטי לבידוד הוא:לכן העובי הקריטי לבידוד הוא:
עבור המצב האידיאלי בו החוט המוליך באמצע הצינור, נוכל למצוא את ההתנגדות לפי הולכה חד-ממדית בקיר גלילי:
עבור החוט הלא מרכזי, ההתנגדות התרמית של הבידוד ניתנת לחישוב בעזרת מקרה 7 בטבלה 4.1, כאשר האי-מרכזיות שלנו היא
: נציב נתונים ונקבל:
לכן, ההתנגדות התרמית של הבידוד ירדה ב-
במקרה הלא אידיאלי.
תרגיל 1
איגלו בצורת חצי כדור, עשוי מבלוקים של קרח, קוטר פנימי
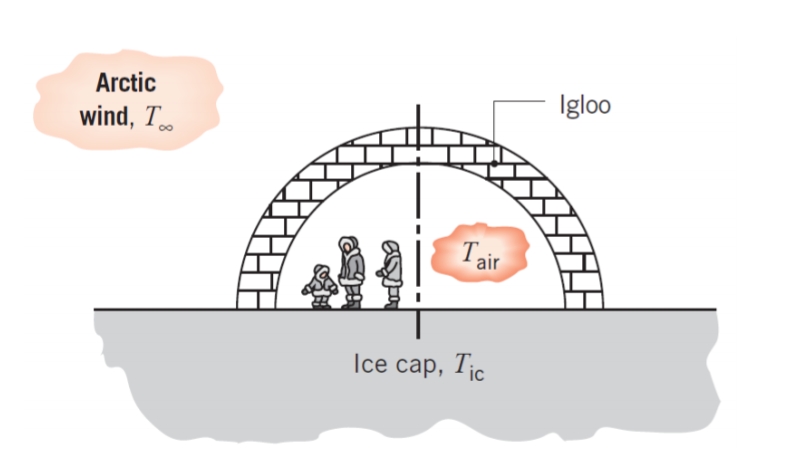
סכמת הבעיה. (Bergman & Lavine, 2017).
האיגלו ממקום על קרחון גדול מאוד בטמפרטורה
בהינתן טמפרטורת האוויר בסביבה
פתרון:
תרשים נגדים שקול למערכת.
אנו יודעים שהחום שהמשפחה מייצרת כולו הולך לקרח ולאוויר מחוץ לאיגלו, ולכן:
מהתרשים נגדים, נסיק כי בחלק העליון:
בחלק התחתון, כאשר עבור במעבר חום לקרח ניעזר בטבלה 4.1 למקדם צורה לדסקה (מקרה 10):
נציב הכל בחזרה בביטוי שקיבלנו עבור