עיקרון אי הוודאות
עיקרון אי הוודאות בא ואומר כי לא ניתן לדעת בוודאות את מיקום האלקטרון ואת התנע שלו בו זמנית. ככל שמיקומו של האלקטרון ידוע בצורה מדויקת יותר, התנע שלו ידוע ברמת דיוק נמוכה יותר:
כאשר
אנלוגיה נחמדה היא מרכוז אור של פנס. ככל שנרכז יותר את אור הפנס, כך נוכל לראות יותר טוב נקודה מסוימת שהפנס מאיר עליה, אבל לא נוכל לראות מסביב לנקודה. ככל שנרכז פחות את האור, נוכל לראות שטח מואר יותר גדול, אבל שטח זה יהיה פחות מואר. אחד בא על חשבון האחר.
עיקרון זה בא לכך מהסיבה שאם נרצה באמת לברר את מיקומו של האלקטרון, נצטרך לשלוח אליו פוטון. אם אורך הגל יהיה גדול מהאלקטרון, לא נוכל לדעת במדויק את מיקומו. אם אורך הגל יהיה קצר מהאלקטרון, נוכל לדעת בוודאות יותר גבוהה את מיקומו, אך הפוטון שפגע באלקטרון הוא בעל אנרגיה גבוהה, ולכן הוא שינה את התנע של האלקטרון, כלומר, אי הוודאות בתנע גדלה.
עיקרון אי הוודאות בא לידי ביטוי רק במימדים ממש קטנים, בממדים הקוונטים, ולכן אין לנו דאגה לגבי מדידותינו על גופים בגדול סטנדרטי, כמו מהירות ומיקום מכונית.
משוואת שרדינגר
ב-1926 התפרסם מאמרו של ארווין שרדינגר, בו הוא מציע משוואת תנועה חדשה לאלקטרונים שזכתה להיקרא על שמו. משוואה זו, תרמה לפיתוח תאוריה יותר מדויקת על תנועת ואנרגית האלקטרונים באטום.
wat
אל דאגה, לא ננסה להבין מה כתוב שם.
מה שחשוב להבין זה שבגדול, המשוואה הזאת היא משוואת תנועה שמתארת כיצד המצב הקוונטי של מערכת פיסיקלית משתנה לאורך זמן (אם תסתכלו ממש טוב, תראו ש-
אורביטל
פונקציית גל של אלקטרון אחד נקראת אורביטל. אורביטל הוא למעשה פתרון של משוואת שרדינגר, והוא מתאר את ההסתברות למצוא אלקטרון באזור מסוים באטום.
לאורביטל 3 מספרים קוונטים, התלויים אחד בשני, ובעזרת שלושת מספרים אלו ניתן למצוא את ההסתברות למצוא אלקטרון מסוים במרחב.
- מספר קוונטי ראשי (
): מתאר את האנרגיה והנפח של האורביטל. . נקרא גם “קליפה”, כיוון שבאמת ככל שמספר הקוונטי יותר גדול, מדובר על אורביטל בעל נפח יותר גדול.
- מספר קוונטי משני (תנע זוויתי,
): מתאר את צורת האורביטל:
עבור
עבור
- מספר קוונטי מגנטי (
): מתאר את כיווניות האורביטל במרחב:
עבור
מס’ קוונטי ראשי,
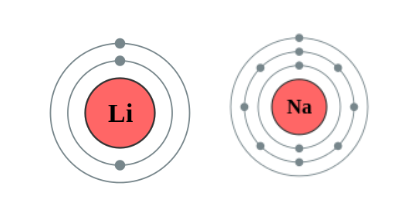
כל עיגול בדיאגרמה זu מציין קליפה אלקטרונית שונה. באטום ליתיום ישנם 2 קליפות, לעומת נתרן שיש לו 3.
מס’ קוונטי משני,
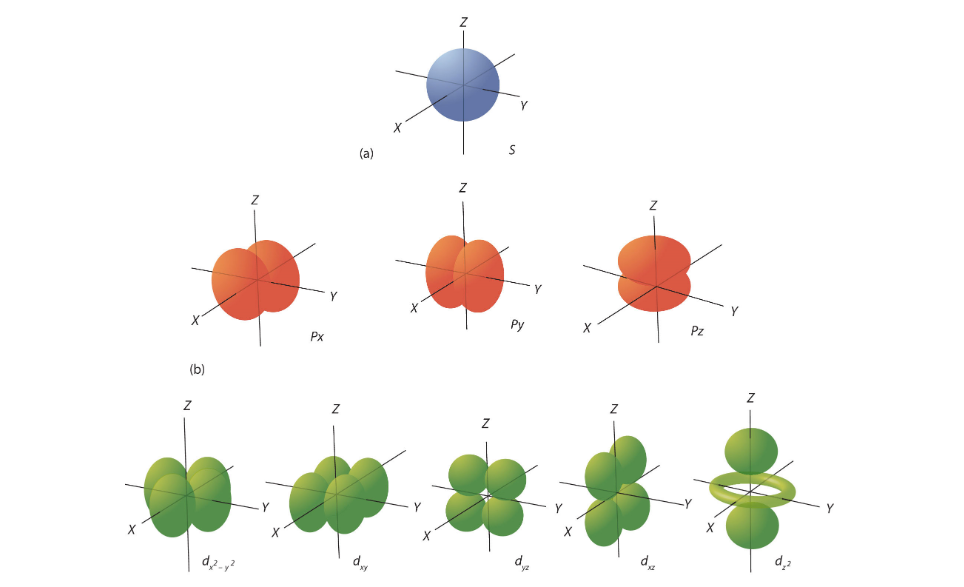
בכל שורה, מדובר בתת-קליפה שונה. ההבדל בין הצורות הוא הכיווניות שלהן. אז איפה הקליפה מיוצגת כאן? עבור כל קליפה קיימים התתי קליפות האלו, עם הכיווניות הללו (כמובן שקיימים עוד תתי קליפות, ועבורן עוד כיווניות משלהן).
מס’ קוונטי מגנטי,
כתיבת אורביטלים
נהוג לכתוב את האורביטלים כך:
כאשר
מספר האלקטרונים שיכולים להיות בכל אורביטל הוא 2:
| קליפה ( | תת-קליפה ( | מספר האורביטלים עבור כל תת-קליפה | מספר האלקטרונים המקסימלי בכל תת-קליפה |
|---|---|---|---|
| 1 | 1 ( | 2 | |
| 2 | 1 ( | 2 | |
| 3 ( | 6 | ||
| 3 | 1 ( | 2 | |
| 3 ( | 6 | ||
| 5 | 10 |
ספין
קיים מספר קוונטי רביעי, אך הוא לא תלוי בשלושת המספרים הקוונטים. מספר זה נקרא הספין של האלקטרון. ניתן לחשוב על הספין כסיבובו של האלקטרון סביב עצמו, כמו שכדור הארץ מסתובב סביב עצמו. האלקטרון יכל להסתובב בשני כיוונים, עם או נגד כיוון השעון, ואם ניזכר בפיזיקה 1, סיבוב זה מייצר שדה מגנטי תוך כדי סיבובו.
אטום רב אלקטרוני
שרדינגר פיתח את משוואת הגל עבור אטום המימן - אטום בעל אלקטרון יחיד. עבור אטום רב אלקטרונים, מתווסף משתנה חדש: כוחות הדחייה בין האלקטרונים.
באטומים אלו, כוחות המשיכה בין הגרעין לאלקטורנים גדלים ככל שמטען הגרעין גדל. כתוצאה מכך האנרגיה של האורביטלים קטנה (יותר שלילית) ככל שהמספר האטומי גדל. בנוסף לעומת מודל בוהר, בו אנרגיית אוריבטל ניתנת רק ע”י
תופעת המיסוך
ניתן לחשוב על זה כך:
- אלקטרונים ממסכים את המטען הגרעיני ביחס לאלטרונים החיצוניים.
- לכן, מטען הגרעין הפועל על אלקטרונים חיצוניים מופחת.
- כלומר, האלקטרונים החיצוניים המרוחקים מהגרעין נמשכים פחות אל הגרעין.
למשל, לאלטרון ב-
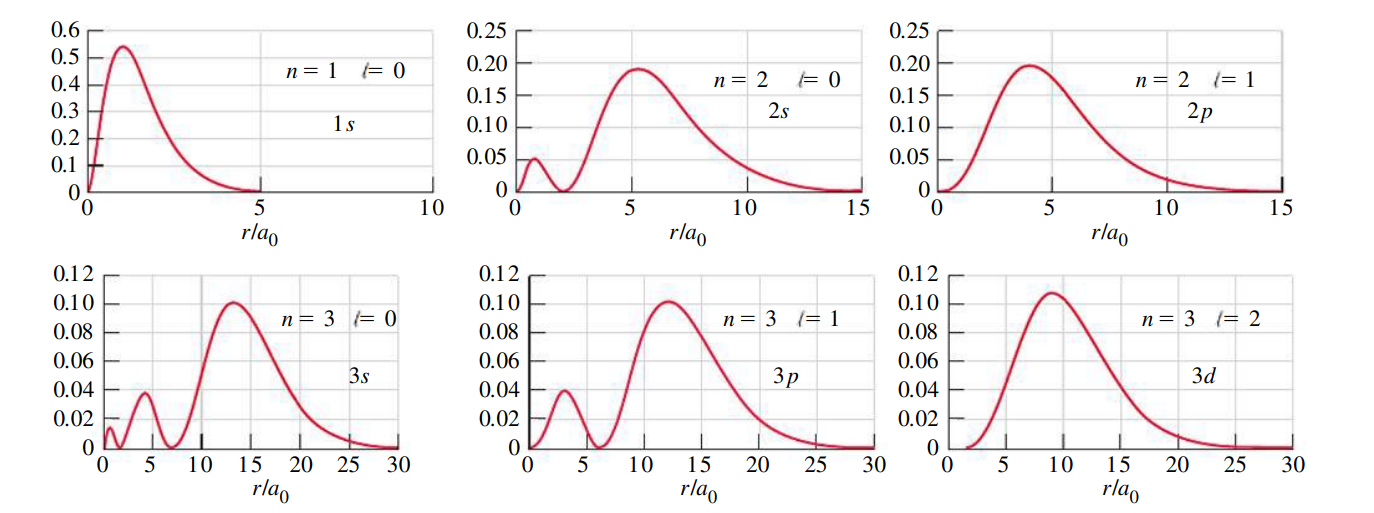
כאן ניתן לראות את ההתסברות למצוא אלטרון באורביטלים שונים. הציר האנכי מתאר את ההסתברות, והציר האופקי מתאר את הקרבה של האלקטרון לגרעין.
אם נשרטט דיאגרמה של האורביטלים השונים כרמות האנרגיה שלהן, אזי נקבל:

כל קו מתאר אורביטל. נשים לב שעבור מימן, המספר הקוונטי המשני לא משפיע על רמת האנרגיה של האורביטל. בנוסף, לכל אטום יש דיאגרמת רמת אנרגיה שונה.
כיוון שאלקטרון תמיד ישאף להיות ברמת האנרגיה הנמוכה ביותר, נוכל לקבוע את הסדר בוא מתמלאים האורביטלים באלקטרונים.
מטען אפקטיבי
מטען אפקטיבי (
כאשר
אלקטרוני ערכיות
אלקטרוני הערכיות הם אותם אלקטרונים חיצוניים שממוסכים מהגרעין. הם משחקים תפקיד מאוד חשוב בקשרים כימיים.
אכלוס אלקטרונים
ישנם 3 חוקים לפיהם מאלכסים את האלקטרונים באורביטלים השונים:
- עיקרון אפבאו - האכלוס האלקטרוני הוא כזה שיוביל לכך שהאנרגיה הכללית של האטום היא המינימאלית האפשרית. כלומר, מאכלסים תחליה אורביטלים בעלי אנרגיה נמוכה ומתקדמים לעבר אורביטלים גבוהים יותר באנרגיה.
ככל שסכום המספרים הקוונטים הראשי והזוויתי -נמוך יותר כך האוביטל נמוך יותר באנרגיה ומאוכלס ראשון.
במידה והסכום זהה לשני אורביטלים מאכלסים קודם את זה בעל המספר הקוונטי הראשי הקטן ביותר.

- עיקרון האיסור של פאולי - לא ייתכנו באטום שני אלקטרונים בעלי אותם ארבעה מספרים קוונטים. בכל אורביטל יכולים להיות לכל היותר 2 אלקטרונים.
בנוסף, אם באורביטל מאוכלסים שני אלקטרונים, הם חייבים להיות בעלי ספין הפוך. - כלל הונד (כלל האוטובוס) - כמו שבאוטובוס נעדיף לשבת איפה שיש שני כיסאות ריקים, גם אלקטרונים באותה רמת אנרגיה יעדיפו “להיכנס” לאורביטל ריק לפני שיצטרפו לאורביטל שיש בו כבר אלקטרון.
קונפיגורציה אלקטרונית
קונפיגורציה אלקטרונית היא הצורה בה האלקטרונים של אטום מסוים מסתדרים בקליפות ובתת קליפות.
ישנם מספר דרכים לייצג את הקונפיגורציה האלקטרונית של אטום מסוים. למשל, עבור פחמן (
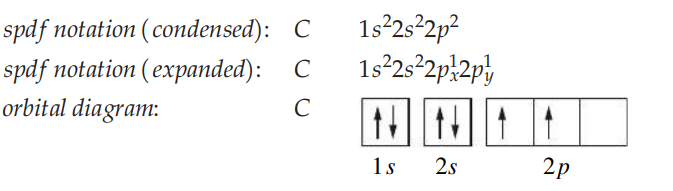
כדי לרשום קונפיגרציה זו, נשתמש בתהליך אפבאו. נתחיל במספר אטומי הראשון, ומשם בסדר עולה נוסיף עוד פרוטון (וגם ניוטרון) לגרעין ונתאר את האורביטל שאלקטרון מתווסף אליו בכל שלב:
-
עבור
, ישנו אלקטרון אחד, ורמת האנרגיה הכי נמוכה של אלקטרון היא אורביטל . אזי הקונפיגורציה האלקטרונית שלו היא . -
עבור
, האלקטרון נכנס לאורביטל כאשר יש לשני האלקטרונים יש ספינים מנוגדים: . -
עבור
, האלקטרון השלישי לא יכל להיכנס לאורביטל (לפי עיקרון פאולי). לכן הוא נכנס לאורביטל הבא, . הקונפיגורציה האלקטרונית היא . -
עבור
, הקונפיגורציה היא . -
עבור
, הקונפיגורציה היא . -
עבור
, הקונפיגורציה היא .
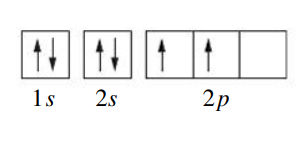
- עבור
, כל התת קליפות מתמלאות:
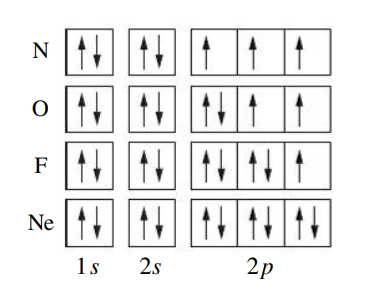
באותו אופן נכתוב את הקונפיגורציה עבור כל שאר האטומים. ניתן גם לכתוב במקוצר את הקונפיגורציה הארוכות ע”י הצבת קונפיגורציה של גז אציל, למשל
