שאלה 1
זהה לשאלה מתרגיל בית.
שאלה 2
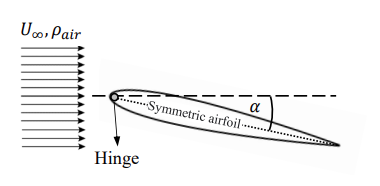
הכנף הנתונה
סעיף א’
לפי מקדם העילוי:
במקרה סימטרי, אנו יודעים כי
מאחר ו-
מהגדרת מקדם העילוי, נסיק כי כוח העילוי ליחידת אורך
סעיף ב’
הכנף סימטרית, ולכן מקדם המומנט ברבע כנף הוא פשוט:
סעיף ג’
מאחר והמומנט ברבע מיתר מתאפס, נסיק ששם פועל מרכז כוח העילוי.
דג”ח על הכנף.
הוא כוח הריאקציה בציר.
נדרוש שסך המומנטים סביב שפת ההתקפה ייתאפסו:
שאלה 3
זהה ל[[FLD1_010 ניתוק זרימה#תרגילים#שאלה 1|שאלה מתרגול]].
שאלה 4
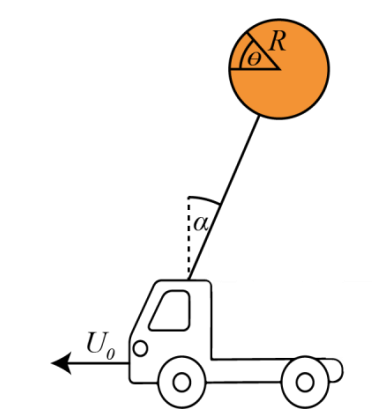
סכימת המערכת
סעיף א’
אם נגדיר את מערכת הצירים שלנו צמוד למרכז הבלון, לפי זרימה סביב גליל שדה הזרימה סביב הבלון יהיה:
כאשר התנאי שפה היחיד שהשתמשנו בו הוא תנאי אי-חדירה ב-
סעיף ב’
נתון כי הזרימה אינרציאלית ואי-רוטציונית, כך שנוכל להשתמש במשוואת ברנולי בין כל שתי נקודות במרחב.
נבחר נקודה רחוקה מספיק, בגובה
סעיף ג’
נמצא את סך הכוח שהלחצים מפעילים על הבלון:
הפונקציה
כלומר, קיבלנו שאין כוח גרר על הבלון:
סעיף ד’
במציאות, יהיה גרר על הבלון כי בשלב מסוים לאורך שכבת הגבול על הבלון, הזרם יתקדם בכיוון המנוגד לגרדיאנט הלחצים - הוא יזרום בכיוון בו הלחץ עולה. למקרה זה אנו קוראים ניתוק, והוא משנה לחלוטין את שדה הזרימה מנקודה זו הלאה.
סעיף ה’
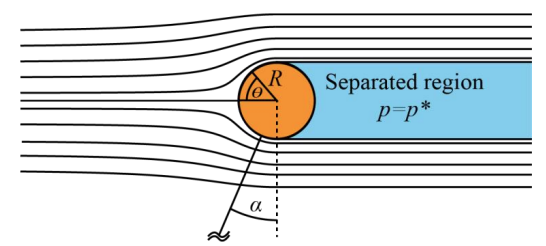
מידול הניתוק
מסעיף ב’ והנתונים החדשים:
באותו אופן כמו בסעיף ג’, נחשב את כוח הגרר, רק הפעם נפרק את האינטגרל:
ולכן:
סעיף ו’
דג”ח על הבלון
מעיקרון ארכימדס, גדלי כוח הציפה והכבידה הם:
בשיווי משקל, מתקיים:
ולכן זווית המיתר היא:
אנו יודעים ש-
שאלה 5
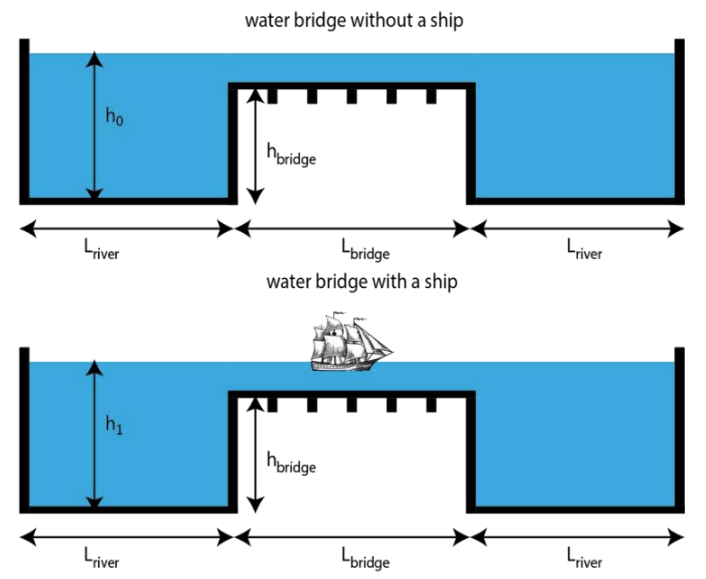
סכימת הגשר
סעיף א’
לפי הגבול ההידרוסטטי, נדרוש ש:
סעיף ב’
לפי עיקרון ארכימדס:
במקרה שלנו:
כלומר, נפח הספינה שנמצא בתוך המים הוא
סעיף ג’
מהידרוסטטיקה בכבידה, נסיק כי הלחץ כתוצאה מהמים על תחתית הגשר הוא (במקרה בלי הספינה):
במקרה עם הספינה:
בהנחה ונפח המים מאוד גדול (
סעיף ד’
נחשב את שינוי הגובה של המים. אנו יודעים שנפח המים שהושפעו הוא:
נתון כי רוחב הבעיה (או עומק, לכיוון המסך) הוא
כעת, מסעיף קודם, השינוי בלחץ הוא:
נציב את הביטוי שמצאנו ל-