| סטודנט א’ | סטודנט ב’ | |
|---|---|---|
| שם | עידו פנג בנטוב | ניר קרל |
| ת”ז | 322869140 | 322437203 |
| דואר אלקטרוני | ido.fang@campus.technion.ac.il | nir.karl@campus.technion.ac.il |
שאלה 1
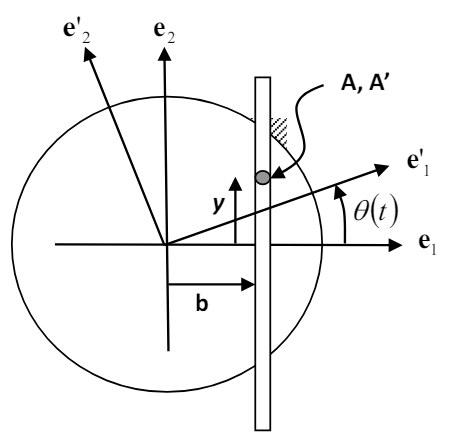
סכימת הדסקה
סעיף א’
נביט ברגע
הנקודה
והמהירות שלה ברגע .
נתון כי
כאשר
ולכן:
כאשר נשים לב שביטוי זה נכון לכל
סעיף ב’
מיקום
לכן, עבור
נעביר למערכת צירים
נציב:
נשים לב ש-
סעיף ג’
המיקום של
לפי משוואות גוף קשיח:
מאילוצי גיאומטריה, אנו יודעים ש-
במערכת
סעיף ד’
את המהירות היחסית נוכל למצוא ע”י חיסור בין
שאלה 2
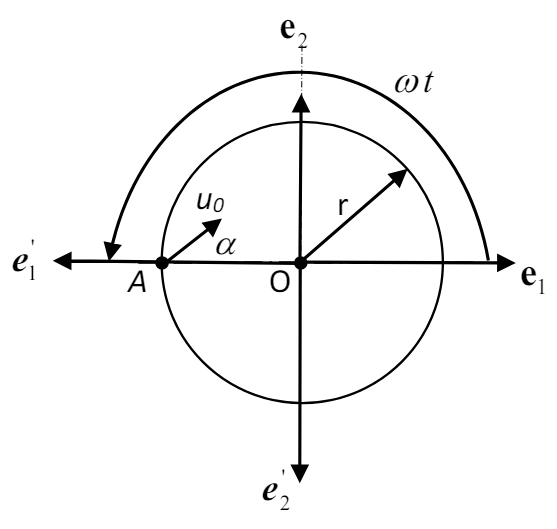
סכימת הדסקה
סעיף א’
המהירות של נקודה
נשים לב ש:
לכן:
בכל
נתון כי הכדור נזרק, ביחס לאדם, במהירות
אבל, כיוון שהאדם עומד על דסקה מסתובבת:
נשים לב שזוהי מהירות הכדור הרגעית לפי מערכת הצירים
נשווה מקדמים:
נסיק כי:
נוכל להציב את
סעיף ב’
מיקום הכדור ב-
בסעיף הקודם מצאנו כי:
ולכן (לאחר אינטגרציה והצבת תנאי התחלה):
כאשר שמנו לב ש:
כי
שאלה 3
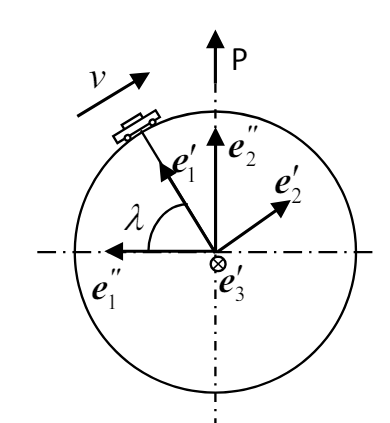
סכימת המכונית וכדור הארץ
דרך א’
לפי הגדרות מערכת הצירים:
נמצא את התאוצה המוחלטת של המכונית במערכת
נשים לב כי לפי הנתונים:
כדי למצוא את
כאשר, לפי הנתונים,
| ולכן: |
נציב בחזרה בביטוי עבור
נתון גם שמהירות המכונית קבועה ובגודל
כאשר
מקשרי גוף קשיח אנו גם יודעים ש:
נשווה בין שני הביטויים עבור
מהשוואת מקדמים:
נציב בביטוי עבור
נציב שוב את
דרך ב’
נבחר במערכת הצירים צמודת המכונית
נייצג את מיקום המכונית במערכת הצירים:
נגזור את המיקום לפי כלל האופרטור:
נשים לב כי:
נמיר את
נציב בכלל האופרטור:
נגזור את הביטוי שוב בעזרת כלל האופרטור כדי למצוא את התאוצה:
הרכיב
נציב בחזרה בכלל האופרטור:
בנוסף אנחנו יודעים שהמהירות היחסית בין המכונית וכדור הארץ היא
מכיוון ש-
שאלה 4
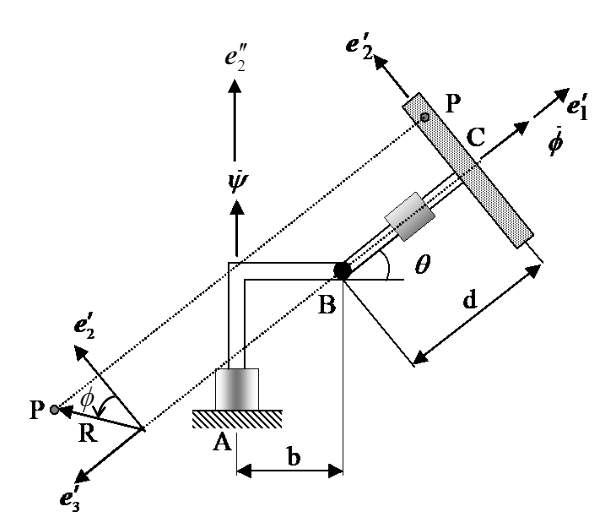
סכימת הדסקה
מערכות הצירים:
סעיף א’
מיקום הנקודה
כאשר
במונחים של
נגזור לפי כלל האופרטור, כאשר נשים לב ש:
| לכן: |
עבור התאוצה, נגזור שוב לפי כלל האופרטור, כאשר נשים לב ש-
| לכן: |
סעיף ב’
נשים לב (לפי השרטוט
לפי כלל האופרטור:
| ולכן: |
כדי למצוא את התאוצה נשתמש שוב בכלל האופרטור, כאשר נשים לב ש-
| ולכן: |
סעיף ג’
תרגיל 5
נשים לב כי:
וגם ש:
ולכן גם:
סעיף א’
נשים לב כי:
לפי חישוב קצב סיבוב:
נחשב כל חלק בנפרד:
ולכן:
סעיף ב’
נשים לב כי:
נחשב כל מכפלה בנפרד:
נסיק שכנראה
נציב נתונים:
קיבלנו:
סעיף ג’
נשים לב כי:
נחשב כל חלק בנפרד:
ולכן: