DYN1_003 קינמטיקה של גוף קשיח

שדה המהירות בגוף קשיח

גוף קשיח הוא גוף רציף של חלקיקים בעל גודל סופי השומר על קבועה.
כל שתי נקודות בגוף שומרות על מרחק קבוע:

לכן אם נגזור את המכפלה שלו בעצמו, נקבל אפס:

כלומר המהירות היחסית ניצבת בהכרח למיקום היחסי.

וקטור מהירות זוויתית רגעית של גוף קשיח

במערכת צירים צמודת-גוף הוקטורים של נקודת חומר הינם קבועים:

אם נגזור במערכת זו:

ה- עבור גוף קשיח במערכת צירים צמודת גוף מספיק מיוחד כדי לתת לו שם:

הגדרה:

נגדיר וקטור מהירות סיבוב רגעית של הגוף הקשיח:

הקשר נכון לכל שתי נקודות גוף כאשר מבוטאות בכל מערכת צירים! הסיבה לכך היא שלכל שני וקטורים ולכל מטריצת סיבוב מתקיים:

כדי לתאר את המהירות הרגעית של כל נקודת גוף מספיק לדעת מהירות של נקודת גוף נתונה ואת וקטור המהירות הזוויתית הרגעית :

ביטוי זה נקרא שדה המהירויות של הגוף הקשיח.
אם נרצה למצוא את התאוצה המוחלטת של נקודה ביחס לתאוצה המוחלטת של הנקודה , לאחר פיתוח נקבל:

וביטוי זה נקרא שדה התאוצות של הגוף הקשיח.

חישוב קצב סיבוב מקינמטיקה של שלוש נקודות בגוף

אם נתונים מיקומים רגעיים ומהירויות רגעיות של 3 נקודות גוף, ניתן למצוא את :
ניקח את הקשר

נכפול וקטורית משמאל ב-:

נפתח את אגף ימין ע”י מכפלה וקטורית משולשת (bac to cab):

אנו יודעים כי , ולכן . נציב:

מביטוי זה ניתן לראות שכדי שנוכל למצוא את המהירות הזוויתית באמצעות נוסחה זו צריכים להתקיים שני תנאים:

1. הנקודות לא יכולים להיות על אותו קו, כי אז מתאפס.
2. המהירות הזוויתית לא נמצאת על המישור הנפרש ע”י הוקטורים .

מציאת מהירות זוויתית שמקבילה למישור

אם מתקיים התנאי הראשון - , אך התנאי השני לא מתקיים, כלומר , אז חייב להתקיים ש- נמצא על המישור של ולכן מהווה צירוף לינארי כלשהו של הוקטורים כלומר:

נמצא את המקדמים:

נכפיל סקלרית את השני האגפים ב- ונקבל:

ולכן:

מכאן נציב ונקבל נוסחה עבור המקרה בו שייך למישור המוגדר ע”י שלוש הנקודות (אשר לא נמצאות על קו אחד):

מציאת רכיב נורמלי של המהירות הזוויתית

בהינתן מיקומים ומהירויות של נקודות גוף, האם ניתן לחשב ?
אנו יודעים כי מתקיים . נפרק את לחלק מקביל וניצב ל-:

כאשר:

נציב במכפלה הוקטורית:

נכפול וקטורית את שני האגפים ב-:

לפי הזהות bac to cab:

נחלק ב-:

נשים לב ש- , ולכן:

לכן, מתוך נתונים, לא ניתן לחשב את , אלא רק את :

תנועת גוף קשיח במישור

טענה:

עבור גוף קשיח מישורי במצב מהירויות רגעי, קיימת נקודת צמודת גוף שמהירותה הרגעית אפס, והיא נקראת מרכז סיבוב רגעי.

כדי למצוא את הנקודה הזאת, נוכל להיעזר בשדה מהירות של הגוף הקשיח:
מחפשים כך ש- :

גוף מישורי כללי עם שתי נקודות והמהירויות הרגעיות שלהן. הנקודה נמצאת על חיתוך הניצבים למהירויות, והיא המרכז הסיבוב הרגעי.

מקרה מיוחד של נקרא תנועה קווית טהורה:

תנועה בורגית רגעית וציר סיבוב רגעי

ציר סיבוב רגעי

טענה:

יהי גוף קשיח בתנועה מרחבית עם נקודת גוף עומדת (). יהי וקטור מהירות זוויתית רגעית , שניתן לרשום כ- .
נקודות גוף הנמצאות על קו שעובר דרך וכיוונו כולן בעלות מהירות רגעית אפס. הקו נקרא ציר סיבוב רגעי.

הוכחה:
נסמן נקודה כללית על הקו (המוגדרת במרחק כללי מ-):

לפי שדה המהירויות:

כלומר, קיבלנו שלנקודה מהירות רגעית אפסית.

דוגמה: נקיפה של סביבון (precession)

סביבון המסתובב סביב וסביב עצמו במהירות זוויתית קבועים.

נתונים:

לכן וקטור הסיבוב הרגעי שלו נתון ע”י:

ציר בורגי רגעי

טענה:

נתון גוף קשיח הנע בתנועה כללית, עם מהירות זוויתית רגעית .
קיים קו של נקודות (צמודות גוף) שכל נקודותיו נעות במהירות שווה המקבילה ל-. קו זה נקרא ציר הבורג הרגעי.

הוכחה:
ראשית, נראה כי לכל נקודות הגוף אותו רכיב מהירות בכיוון .
ניקח שתי נקודות גוף כלליות . נשים לב כי מתקיים:

ואכן קיבלנו כי:

כעת נרצה למצוא את המקום הגיאומטרי של נקודות גוף אשר נעות בכיוון בלבד. בהינתן נקודת גוף ומהירותה , נסמן:

מחפשים נקודת גוף שמהירותה . נשתמש שוב בקשרי גוף קשיח:

נכפול וקטורית ב- משמאל:

נחלק ב- ונעביר אגפים:

נפרק את לחלק מקביל וניצב ל-:

נשים לב כי . נציב בביטוי שקיבלנו:

כלומר קיבלנו ביטוי לחלק הניצב ל- של . למעשה, נוכל לומר שלכל :

מערכת הצירים המוגדרת ע”י ו-.

נשים לב כי הוא למעשה מהירות הציר הבורגי. את היחס נהוג לסמן ב- - פסיעה:

במקרה המישורי, בו גוף מסתובב סביב , לכל נקודה מתקיים:

(כי אנחנו במקרה מישורי, אנחנו לא יכולים לזוז בניצב למישור). לכן, ציר הבורג הרגעי הוא ציר הסיבוב הרגעי. הנקודה במישור הלוח שבה חותך ציר הבורג/סיבוב הרגעי היא מרכז הסיבוב הרגעי.

וזוהי למעשה הנוסחה למציאת מיקום מרכז הסיבוב הרגעי, בהינתן .

דוגמה:

נתון כי:

מצאו את מרכז הסיבוב הרגעי כתלות ב-.
פתרון:

מקרים פרטיים:

• אם מרכז הסיבוב הרגעי ב-.
• אם , מרכז הסיבוב הרגעי בפינה העליונה של הגוף.
• אם , מרכז הסיבוב הרגעי נמצא באינסוף, שזה שקול פשוט למקרה של תנועה קווית טהורה במהירות .

דוגמה: מסוק טס אופקית

דוגמה מ(Elata, 2002).
מסוק טס אופקית במהירות והרוטור שלו שרדיוסו מסתובב בקצב יחסית למסוק. חשב את מיקום וכיוון הציר הרגעי של הרוטור ואת מהירות הציר.
פתרון:
קצב סיבוב הרוטור הוא:

מהירות מרכז הרוטור היא . לכן, מיקום ציר הסיבוב הרגעי:

מהירות ציר הסיבוב:

תרגילים

שאלה 1

נתונות 3 נקודות על גוף קשיח:

ומהירויותיהן:

סעיף א’

האם שדה המהירויות הנתון יתכן בגוף קשיח?
פתרון:
אנו יודעים שבגוף קשיח המהירות היחסית בין כל 2 נקודות ניצב למיקום היחסי. כלומר, נבדוק שלכל זוג מתקיים (לא סכימה של איינשטיין, נטו סימון):

סעיף ב’

מהו וקטור המהירות הזוויתית של הגוף?
פתרון:
עבור 3 נקודות ניתן להשתמש בנוסחה עבור מהירות זוויתית:

נחשב את המכנה בנפרד:

לכן נוכל להמשיך להשתמש בנוסחה כדי לקבל:

סעיף ג’

מהי משוואת ציר הבורג במרחב?
פתרון:
תהי נקודה כלשהי על ציר הבורג. נרצה למצוא משוואה פרמטרית המייצגת אותה. נבחר את נקודה להיות נקודת הייחוס. לפי ציר בורגי רגעי:

נמצא את :

נמצא את :

נציב ונקבל את :

ולכן משוואת ציר הבורג:

סעיף ד’

באיזו נקודה חותך ציר הבורג את המישור ?
פתרון:
נרצה למצוא עבור איזה ערך של רכיב של מתאפס:

נציב חזרה ל- ונמצא כי נקודת החיתוך הינה:

סעיף ה’

מהי מהירות הגוף הקשיח במקביל לציר הבורג ?
פתרון:
כיוון ציר הבורג הינו , ומהירות הנקודות על הגוף הקשיח הינה אחידה לכיוון ציר הבורג לכן מספיק לחשב את היטל מהירות נקודה אחת בכיוון ציר הבורג:

כלומר הגוף הקשיח אינו מתקדם בכיוון ציר הבורג אלא רק מסתובב סביבו ברגע הנתון.

שאלה 2

אל מוט המסתובב במהירות זוויתית קבועה מחובר גלגל בעל רדיוס . הגלגל מוטה בזווית (קבועה). נקודת המגע שלו עם הרצפה נמצאת במרחק מהראשית. הגלגל אינו מחליק.

נתונים .

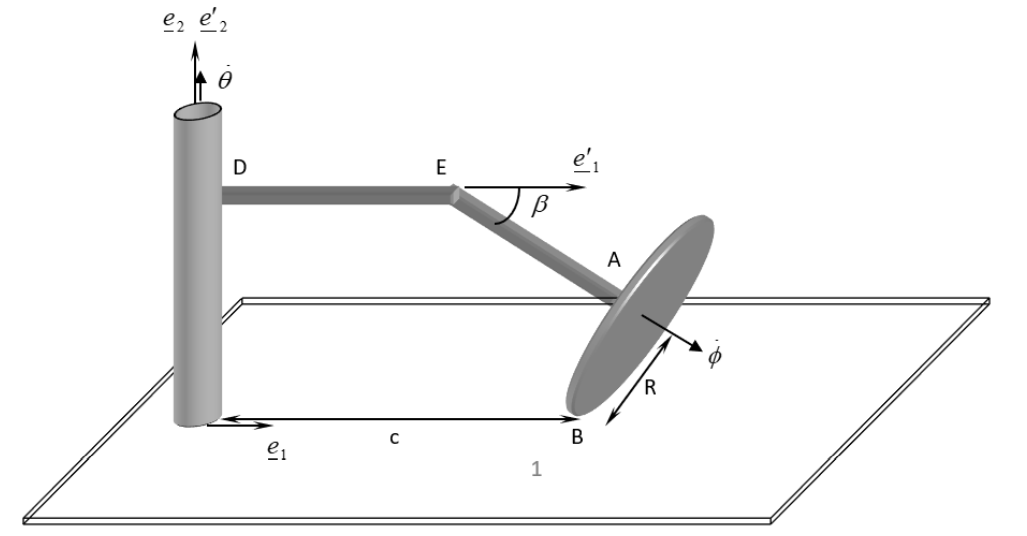
סכמת הבעיה

סעיף א’

מצא את המהירות הזוויתית של הגלגל ביחס ל-.
פתרון:
לשם נוחות נצמיד מערכת צירים למוט , כאשר ומתקיים:

מתקיים ש- מסתובבת באותה מהירות כמו ולכן:

עלינו למצוא את - נוכל לעשות זאת ע”י ניתוח המהירות של מרכז הגלגל , פעם אחת מנקודת מבט של הגוף הקשיח ופעם אחת מנקודת מבט של הנקודה.

• מציאת מנקודת המבט של הגוף הקשיח:
  נמצא את מהירות ביחס לנקודה : לפי גוף קשיח: קיבלנו:
• מציאת מנקודת המבט הגיאומטרית של הנקודה:
  מיקום הנקודה הוא: נמצא את בעזרת כלל האופרטור - כאשר נשתמש ב- . נבנה טבלה:

קיבלנו:

נשווה בין שתי הערכים ל- שקיבלנו:

סעיף ב’

מהי המהירות הזוויתית המוחלטת של הגלגל?
פתרון:
המהירות הזוויתית המוחלטת של הגלגל הינה . נציב את ונקבל:

סעיף ג’

מהי התאוצה הזוויתית של הגלגל?
פתרון:
נשתמש בכלל האופרטור על מנת למצוא את התאוצה הזוויתית, מיוצג במערכת :

נשתמש בטבלה, כאשר נשים לב כי קבוע:

לכן התאוצה הזוויתית היא:

סעיף ד’

מהו ציר הסיבוב הרגעי של הגלגל?
פתרון:
תהי נקודה שרירותית על ציר הבורג. נשים לב כי היא נקודה נייחת (רגעית) על הגוף הקשיח. לכן נחשב את ביחס ל-:

נשים לב כי ציר הסיבוב נמצא על מישור ועובר דרך נקודה . בנושא הבא תוצאה זו מסתדרת עם הנושא של גלגול ללא החלקה.

שאלה 3

מוט שאורכו מחובר בשני קצותיו לגלגלות ו-. הגלגלת נעה לאורך קטע ישר והגלגלת נעה בקטע חצי מעגלי ברדיוס . נתון כי הקצה נע במהירות שגודלה קבוע ושווה בכיוון המשיק למעגל עם כיוון השעון.

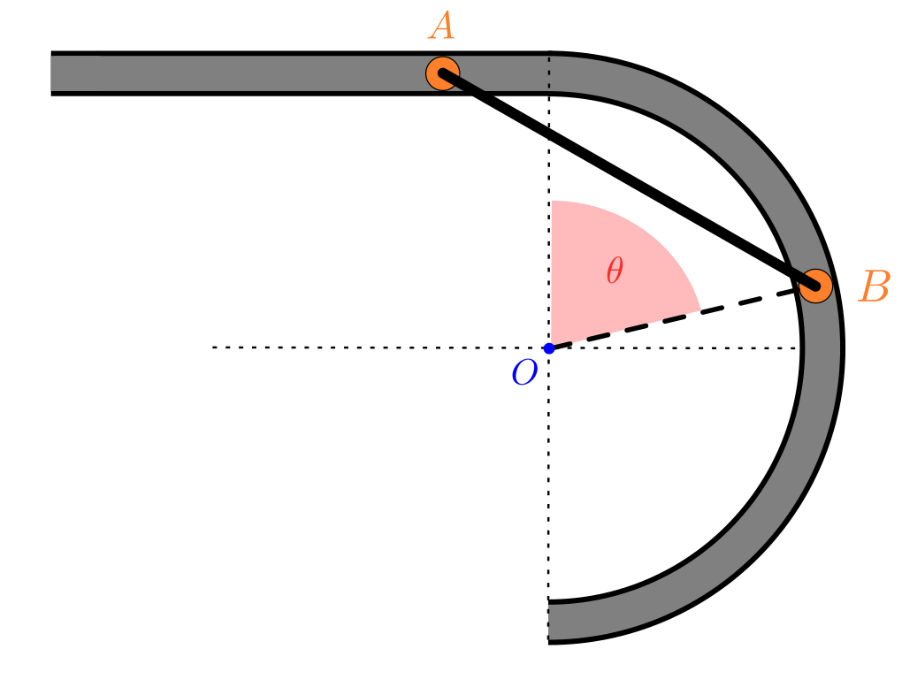
סכמת הבעיה

נתונים .

סעיף א’

מהי המהירות הזוויתית של המוט והמהירות המוחלטת של גלגלת כתלות ב- ובנתונים? הביעו את התשובה בקואורדינטות קרטזיות.

פתרון:

הגדרת מערכות הצירים

נגדיר מערכת צירים כך ש- . לכן:

נגדיר גם מערכת צירים כך ש- :

כאשר היא הזווית בין ל-.

נשים לב כי תחת אילוצי הגאומטריה:

לפי סיבוב רגעי:

ולכן:

אנו יודעים שהנקודה מאולצת לנו אך ורק בכיוון , ולכן נקבל שתי משוואות

עם שלושה נעלמים .
נוכל למצוא עוד משוואה באמצעות אילוץ גיאומטרי. נבנה את משולש באופן הבא:

משולש

מטריגונומטריה מתקיים:

בנוסף:

נציב את בשתי המשוואות ונקבל:

עבור הנעלמים , נפתור ונקבל:

מכאן:

סעיף ב’

מהי התאוצה הזוויתית של המוט והתאוצה המוחלטת של גלגלת כתלות ב- ובנתונים בקואורדינטות קרטזיות?
פתרון:
נשתמש במשוואת גוף קשיח לתאוצה:

כאשר התאוצה של גלגלת מאולצת להיות בכיוון ולכן:

• נתחיל מלמצוא את .
  לפי כלל האופרטור, כאשר : נגזור שוב: נוכל גם למצוא את מהנתון שגודל מהירות הגלגלת קבועה ושווה : ולכן:
• נמצא את :
• נמצא את :

נציב ונקבל:

מכאן נקבל שתי משוואות בשני נעלמים :

לאחר הצבות והרבה אלגברה מגעילה, נקבל אלגברה מגעילה עוד יותר:

לגבי , אין לי כוח.