מחזורי קירור על בסיס קיטור
מטרת מערכות קירור כמו מזגנים ומקררים היא לשמור באזור מסוים על טמפרטורה יותר קרה מאשר סביבתה. לרוב, זה מתבצע ע”י מערכות קירור על בסיס קיטור בהם נעסוק בפרק זה.
מחזור קירור קרנו
כדי להדגים חלק מהרעיונות במחזורי קירור, נביט קודם במחזור קירור קרנו. המחזור מתקבל מהפיכה של מנוע קרנו:
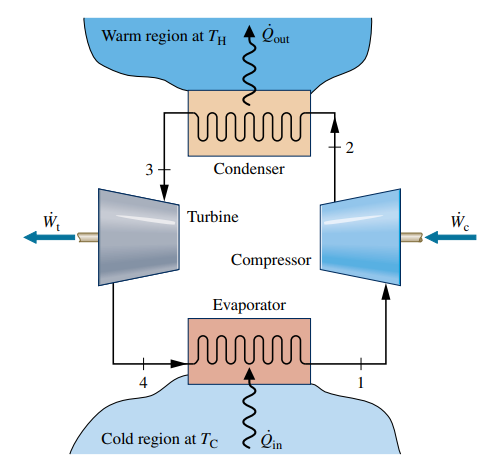
סקיצה של מחזור קרנו.
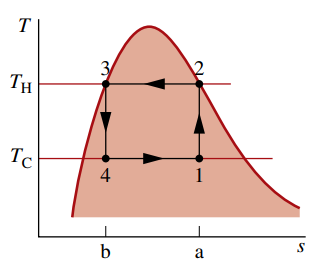
דיאגרמת
של מחזור קירור קרנו על בסיס קיטור.
נעקוב אחרי נוזל הקירור שעובר דרך כל אחד מחלקי המחזור, כאשר נתחיל בכניסה למאייד.
הנוזל קירור נכנס דרך למעבה במצבו הדו-פאזי - מצב
לאחר מכן, נוזל קירור נדחס באופן אדיאבטי ממצב
הנוזל קירור עובר מהמדחס למעבה, בו הוא משנה פאזה מאד רווי לנוזל רווי כתוצאה ממעבר חום בטמפרטורה
לבסוף, הנוזל קירור חוזר למצב ההתחלה בכניסה למאייד כאשר הוא מתפשט אדיאבטית דרך הטורבינה, והטמפרטורה שלו יורדת מ-
מאחר ומחזור זה מורכב מתהליכים הפיכים, ניתן לומר שהשטחים בדיאגרמת
מקדם הביצועים של מחזור הוא היחס בין התוצר להשקעה. כלומר, מהחום שהצלחנו להוציא מהמאגר הקר לסך העבודה שהושקעה במחזור:
כלומר, קיבלנו את המקדם ביצועים קרנו שכבר ראינו בעבר:
איך מחזורים אמיתיים שונים ממחזור קרנו
מחזורי קירור על בסיס קיטור אמיתיים לא באמת יכולים לפעול כמו מחזור קרנו, ובכך הם בעלי מקדמי ביצועים הרבה יותר נמוכים ממנו. הנה מספר סיבות לכך:
- במערכות ריאליות, האינטראקציות חום בין הנוזל קירור למאגרים לא מתקיימים בצורה הפיכה כפי שהנחנו לעיל. למעשה, כדי להשיג קצב מעבר חום מספיק מהיר כדי לשמור על הטמפרטורה הקרה
לרוב נדרשת שטמפרטורה של הנוזל קירור תהיה יותר נמוכה מ- . באותו אופן עבור :
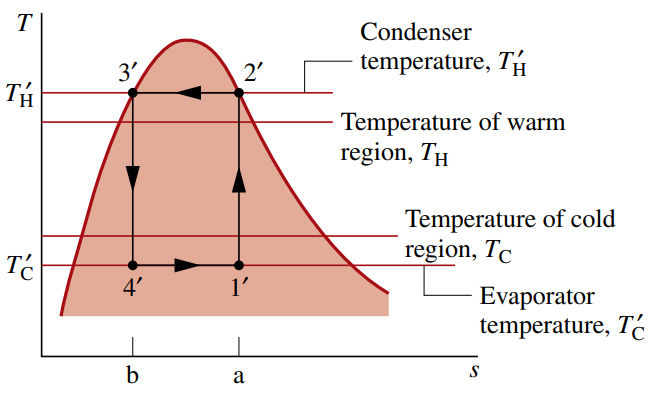
השוואה בין הטמפרטורות של הנוזל קירור במאייד והמעבה עם אלה של המאגרי חום.
- גם כאשר לוקחים בחשבון את הפרשי הטמפרטורות בין הנוזל קירור למאגרים החמים והקרים, ישנם מאפיינים אחרים שהופכים את המחזור קירור קרנו ללא בר ביצוע. כאשר בדיאגרמה האחרונה, נשים לב שהדחיסה ממצב
למצב מתרחשת כולה בתוך הפעמון. לדחיסה כזאת קוראים דחיסה רטובה, ולרוב נרצה להימנע מדחיסה כזאת כי כמו בטורבינה, טיפות המים הקטנות גורמות לשחיקה. לכן, נרצה שהמדחס שלנו יעבוד מימין לפעמון, כך שהנוזל קירור כולו הוא אד שחון, מה שנקרא דחיסה יבשה. - עוד נושא חשוב הוא תהליך ההתפשטות מנוזל רווי במצב
לתערובת נוזל-אד באיכות נמוכה במצב . התפשטות זו בקושי מייצרת עבודה, ולכן מטעמים כלכליים פשוט מניחים שם שסתום.
- גם כאשר לוקחים בחשבון את הפרשי הטמפרטורות בין הנוזל קירור למאגרים החמים והקרים, ישנם מאפיינים אחרים שהופכים את המחזור קירור קרנו ללא בר ביצוע. כאשר בדיאגרמה האחרונה, נשים לב שהדחיסה ממצב
את נקודות אלו אנו מפנימים בנושא הבא, העוסק במחזורי קירור יותר ריאליים.
מחזור קירור על בסיס דחיסת קיטור
מחזורי קירור על בסיס דחיסת קיטור (vapor-compression refrigeration) הן המערכות הכי נפוצות בשימוש כיום. להלן סקיצה של אחת:
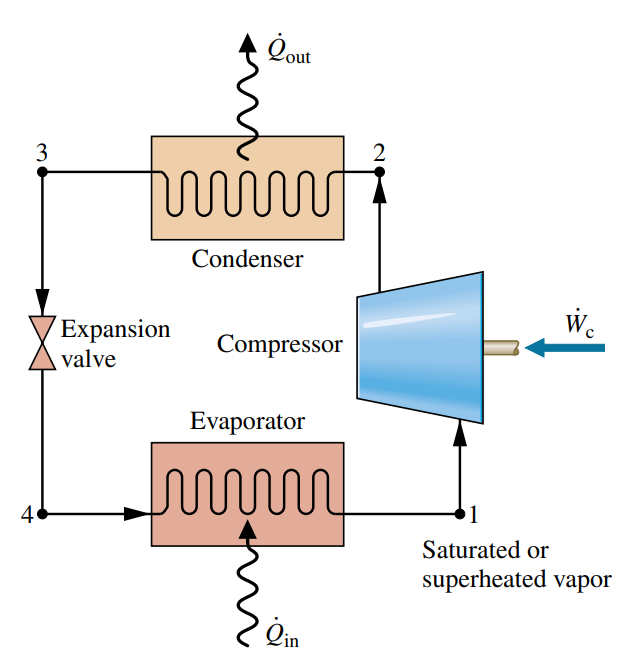
הרכיבים של מחזור קירור על בסיס דחיסת קיטור.
בדומה מאוד למחזור רנקין, נוכל מחוק ראשון במערכת במצב מתמיד לחשב את השינוי באנתלפיות בין כל מצב, כאשר אנו מניחים שהתהליכים אידיאליים:
כאשר את המשוואה
המקדם ביצועים מוגדר כתוצר ביחס להשקעה, ולכן במקרה שלנו:
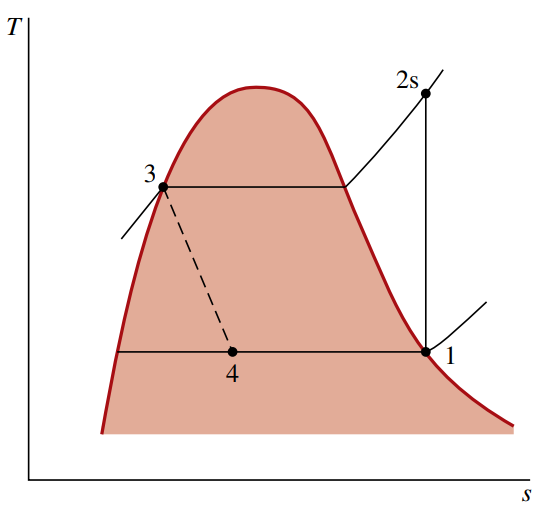
דיאגרמת
של מחזור דחיסה על בסיס דחיסת קיטור אידיאלי.
דיאגרמת
בתחום הקירור, לדיאגרמות
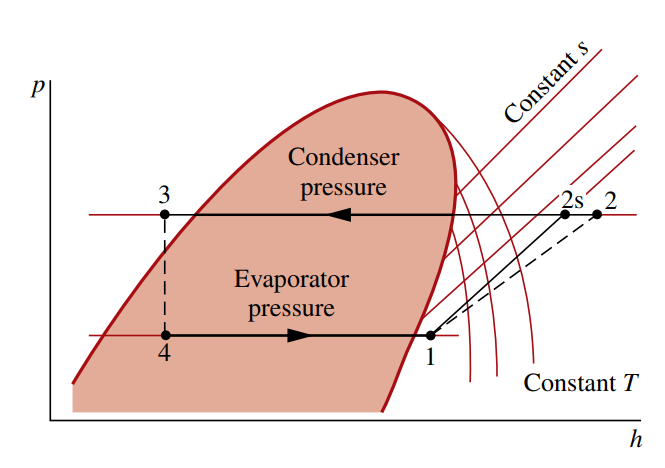
דיאגרמת
עבור מחזור קירור על בסיס דחיסת קיטור.
נשים לב שכמו בדיאגרמת p-v, האיזותרמות בתוך הפעמון שלנו הן קבועות. בנוסף, מתוארים גם הקווי איזנטרופיה שבהן נוכל להיעזר כדי להעריך כמה לא הפיך המחזור שלנו.
תרגיל:
מחזור קירור שכולל מדחס, מעבה, מאייד ושסתום הצערה מפיק
ממציא מציע 2 שיפורים למערכת הנ”ל:
- ביצוע הדחיסה בשתי דרגות עם קירור ביניים עד
בלחץ . - שימוש בטורבינה בעלת דרגת טיב אדיאבטית של
במקום השסתום.
- תארו את המחזור בדיאגרמת
ו- . - חשבו את קצב זרימת האמוניה דרך הטורבינה.
- חשבו את סה”כ עבודת הדחיסה במחזור.
- חשבו את עבודת הטורבינה.
- חשבו את מקדם הביצוע עבור שני המקרים.
- השוו את מקדמי הביצוע עם זה של מקרר הפיך הפועל בין אותם מאגרים.
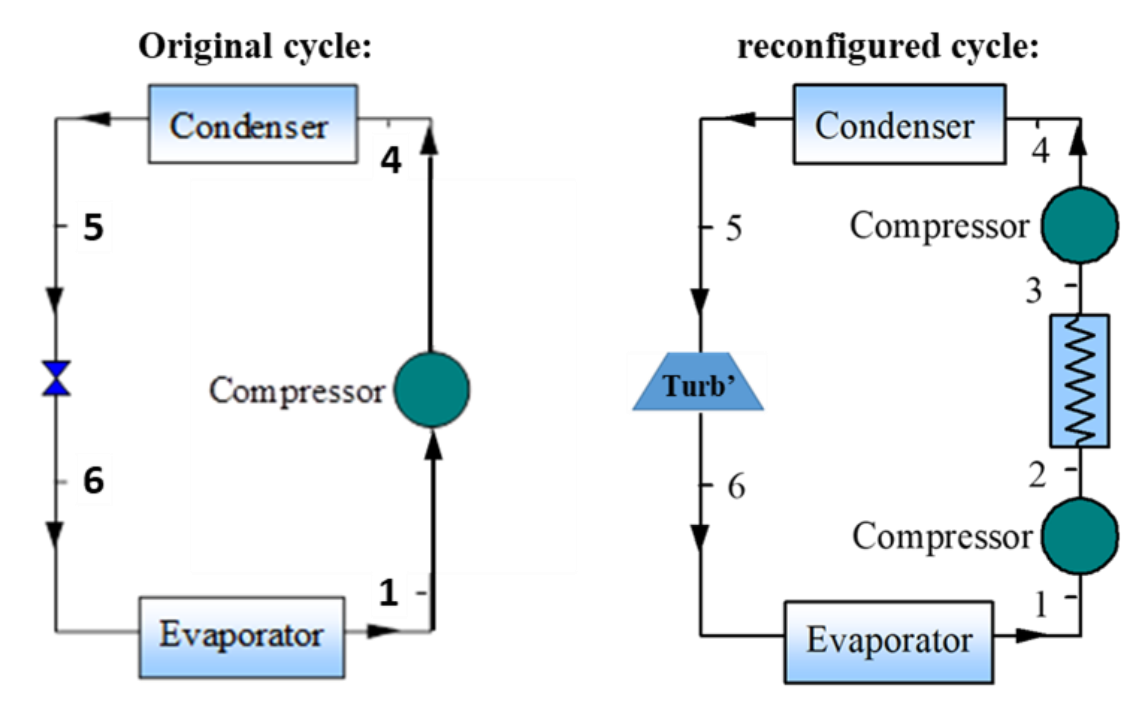
סקיצה הנתונה עם התרגיל.
פתרון:
נשים לב שהנתון
-
נמצא את המצבים בכל אחד מהשלבים. נתחיל ממצב
- בו נתון ש- ו- . מטבלאות אמוניה, נקבל כי: במצב
, המצב האיזנטרופי השקול גם כן מתקבל מטבלאות אמוניה: מהגדרת דרגת הטיב של מדחס:
נציב את
ונקבל: ולכן:
עבור מצב
, נתון כי , ו- . לכן, מטבלאות אמוניה: עבור מצב
, נמצא את המצב האיזנטרופי . מחישובים שאין לי כבר כוח להראות, נראה כי: עבור מצב
, הלחץ נשמר, ומהמעבה יוצא נוזל רווי, כך ש- ו- . לכן, מטבלאות אמוניה ואינטרפולציה: עבור מצב
, נשים לב ש- , כי אנו בתוך הפעמון, ובכך נמצאים באיזותרמה ביחס למצב . שוב, מדרגות טיב, חישוב מצב איזנטרופי שקול ובלה בלה בלה מקבלים: נסכם:
נוכל כעת לשרטט דיאגרמות
ו- :
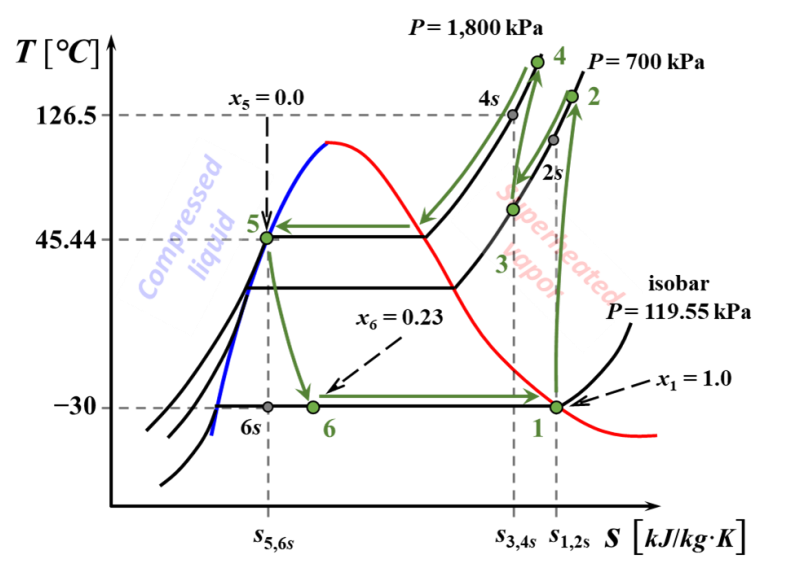
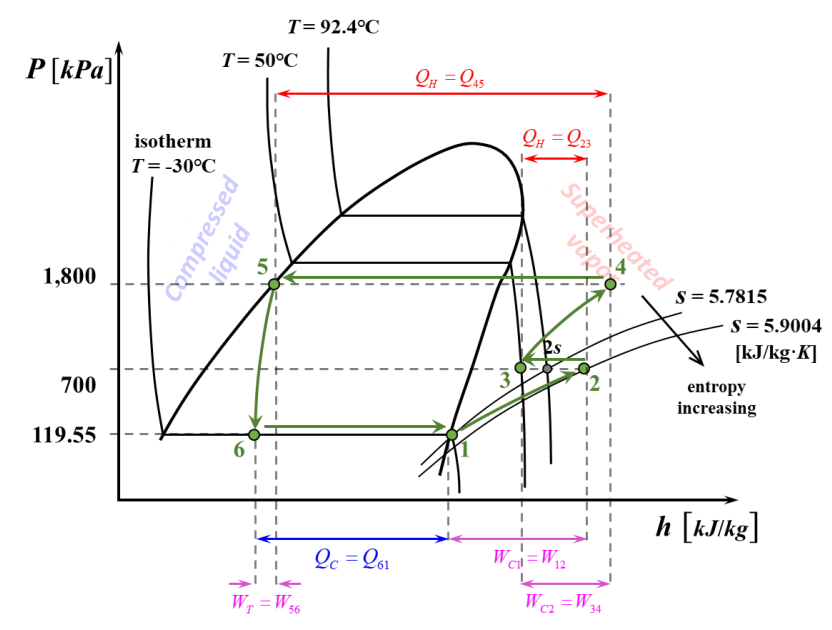
>דיאגרמותו- שניתנו ע”י דוד חסין המל-מל-מלךךך. -
נפעיל חוק ראשון על תהליך
(בתהליך מתמיד): נתון כי
. נציב גם את שאר הערכים ונקבל כי: -
נבצע חוק ראשון על שני המדחסים:
באותו אופן עבור המדחס בין
: נציב ונקבל:
-
נפעיל שוב חוק ראשון ונקבל:
ולכן:
-
מקדם הביצועים של המקרה עם שני מדחסים:
ולכן:
באותו אופן עבור המקרה עם המדחס היחיד:
-
נידרש לחשב את מקדם הביצועים של מחזור קרנו:
נשים לב כי:
אנו לא בוחרים בהכרח בטמפרטורות הכי נמוכות והכי גבוהות במחזור! נבחר דווקא את הטמפרטורות של המאגרים, כי לפיהם מחשבים את נצילות מחזור קרנו. נציב ונקבל: