תחנות כוח על בסיס קיטור
נביט במערכות השונות שמרכיבות תחנת כוח על בסיס דלק:
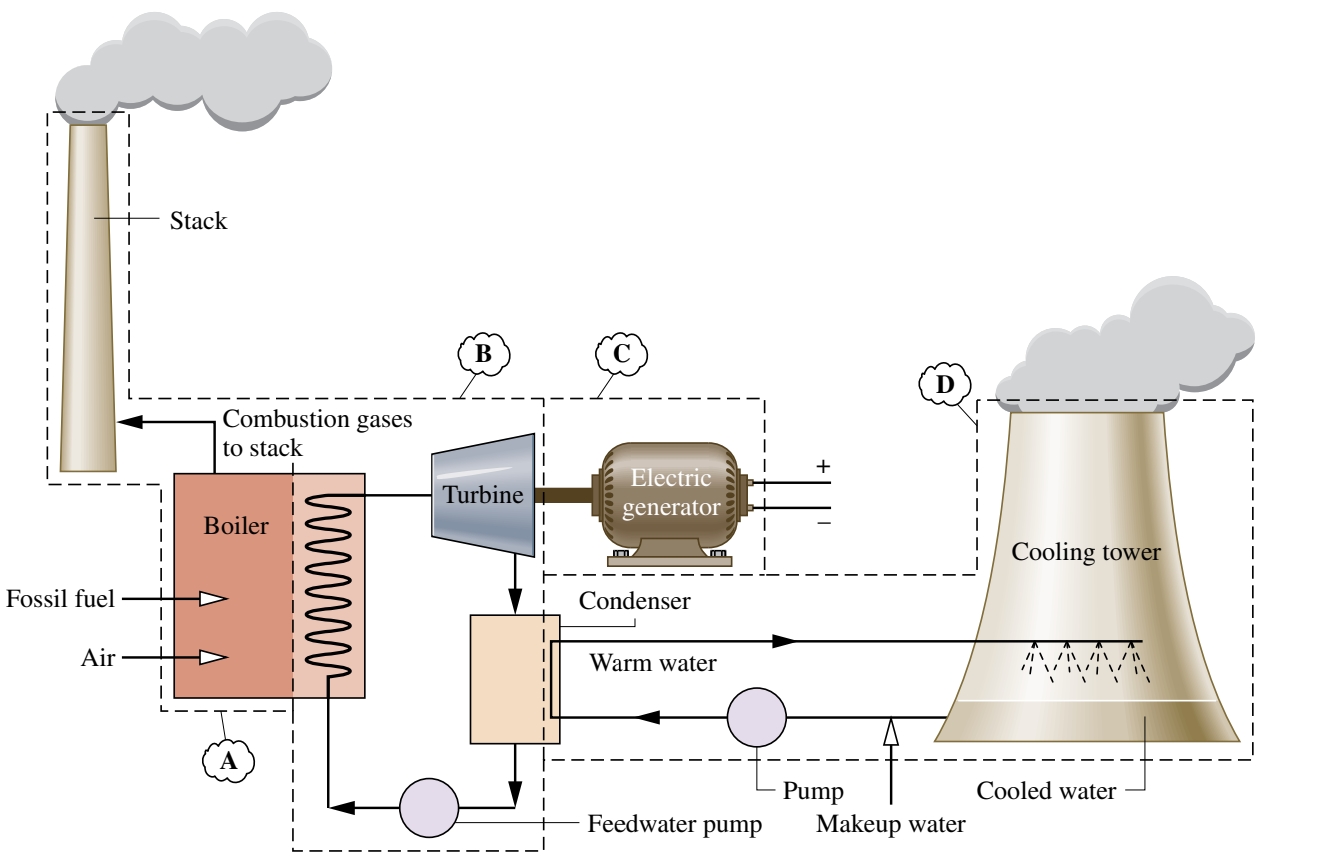
ארבעת המערכות מסומנות באותיות
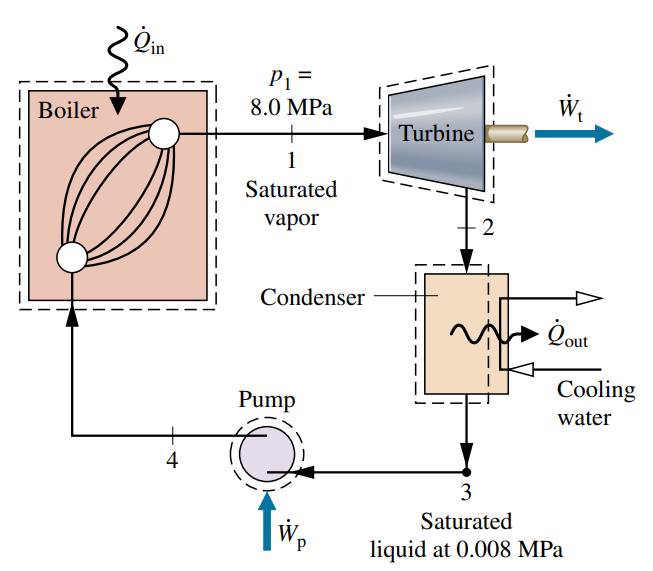
בתחנות כוח על בסיס דלק, התאדות מתבצעת ע”י אינטראקציית חום אל המים העוברים דרך הצינורות מהגזים החמים הנוצרים מבערת הדלק.
האדים העוברים דרך הטורבינה ב-
מעגל הנוזל המקרר נמצא במערכת
מחזור רנקין
נביט במערכת
נציג סכמה פשוטה של מערכת זו:
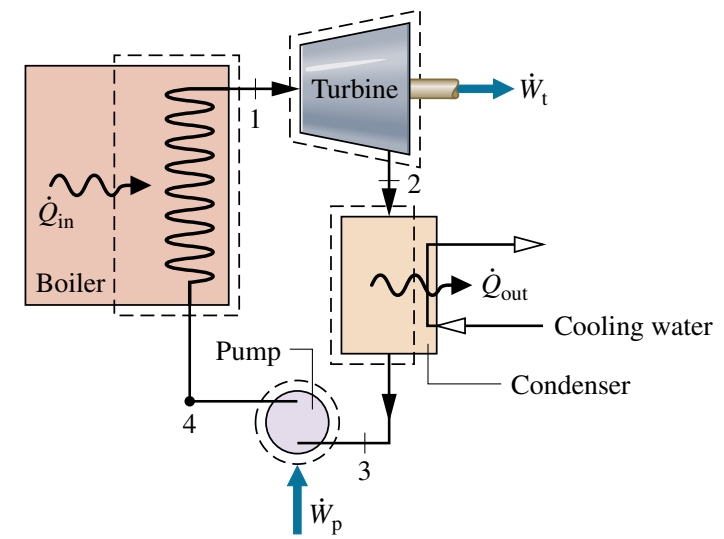
הערות:
- על פי הסכם סימונים, האינטראקציות המסומנות חיוביות בכיוון החץ, חוץ מהמשאבה! הספר מגדיר את סימן העבודה שהמשאבה מבצעת באופן הפוך ממה שאנו רגילים אליו, ומאיך שמוגדר בקורס. כלומר, לפי הסכם סימוני הקורס, החץ של המשאבה בכיוון הפוך ממה שמופיע באיור.
- ספרויות שונות מגדירות את
במקומות שונים, לכן הסימונים האלו כאן לא בהכרח יהיה עקביים עם החומר בקורס. בכללי, כדאי להפנים מה כל אחד מהסימונים האלה מייצג, כדי שתוכלו לפתח את הנוסחאות מחדש עבור המקרים הספציפיים שבהם אתם נתקלים.
אינטראקציות חום ועבודה
אנו נזניח את אינטראקציית חום בין חלקי המערכת לסביבה. בנוסף, נתעלם גם משינויים באנרגיה הקינטית והפוטנציאלית. נתייחס לכל חלק במערכת כפועל בתהליך מתמיד. נעבור חלק חלק ונרשום עבורו חוק ראשון:
- טורבינה - כמו שראינו כבר בפרקים קודמים, עם ההנחות שביצענו, וההזנחה של מעבר חום עם הסביבה:
כאשר , וה- נועד להדגשה שזוהי העבודה המתבצעת ע”י הטורבינה. - מעבה - במעבה יש אינטראקציית חום בין הקיטור לנוזל מקרר העובר בזרם אחר. הקיטור מתעבה והטמפרטורה של הנוזל המקרר עולה. בתהליך מתמיד, לפי חוק ראשון, עבור הנפח בקרה המכיל את החלק המעובה של המחליף חום:
כאשר . האינטראקציית חום חיובית בכיוון החץ. - משאבה - הנוזל המעובה שעוזב את המעבה ב-
נשאב החוצה לדוד בלחץ גבוה. הנפח בקרה מסביב למשאבה מקיים לפי חוק ראשון למשאבה (כאשר אנו מניחים כי אין מעברי חום עם הסביבה): כאשר , ו- נועד להדגשה שזוהי העבודה המתבצעת ע”י המשאבה (pump). - דוד - הנוזל עבודה (מים/קיטור) מסיים את המחזור כאשר הנוזל העוזב את המשאבה ב-
, הנקרא מי הזנה,מחומם לרוויון ומאודה בדוד. נבחר נפח בקרה המכיל את הדוד. לפי חוק ראשון: כאשר .
הגדרה:
נגדיר את היעילות של מחזור זה כמידת האנרגיה שנכנסת לדוד ומומרת לעבודה:
בעזרת המשוואות שפיתחנו:
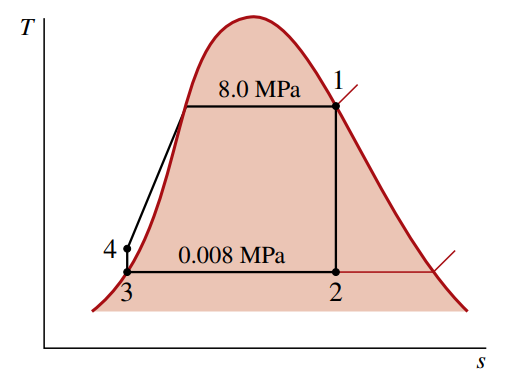
מחזור רנקין אידיאלי
אם הנוזל עבודה (קיטור) עובר במערכות השונות ללא אי הפיכויות כלשהן, החיכוך עם הדוד והמעבה לא יהיה קיים, והנוזל יזרום דרך חלקי המערכת בלחץ קבוע. בנוסף, ללא אי הפיכויות ואינטראקציות חום עם הסביבה, התהליך בטורבינה והמשאבה יהיה איזנטרופי.
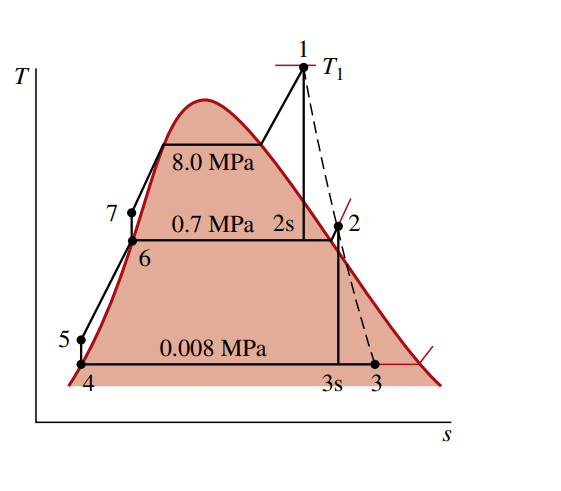
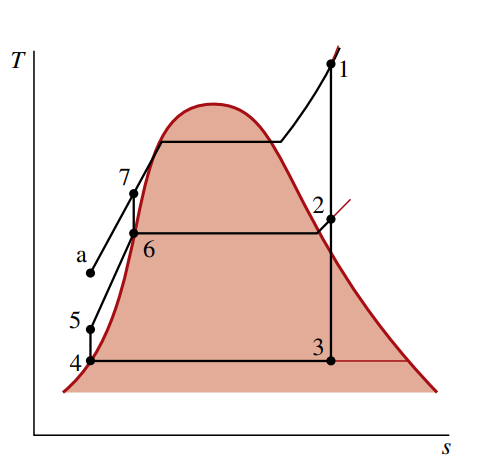
מחזור כזה ייקרא תהליך רנקין אידיאלי, והוא מתואר ע”י הגרף הבא:
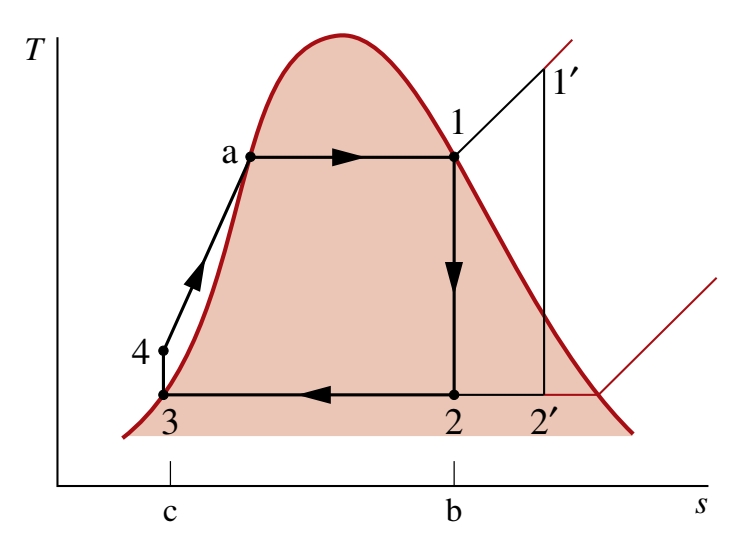
- תהליך
: התפשטות איזנטרופית של הנוזל עבודה דרך הטורבינה מאד רווי במצב ללחץ המעבה. - תהליך
: ישנו מעבר חום מהנוזל עבודה אל הנוזל קירור כאשר הוא זורם בלחץ קבוע דרך המעבה ועוזב כנוזל רווי במצב . - תהליך
: דחיסה איזנטרופית מהמשאבה אל מצב באזור הנוזל הדחוס. - תהליך
: ישנו מעבר חום אל הנוזל עבודה כאשר הוא זורם בלחץ קבוע דרך המשאבה כדי להשלים את המחזור.
על המצבים
מאחר ומחזור רנקין האידיאלי מורכב מתהליכים הפיכים פנימית, ניתן לחשוב על השטח מתחת לקווים המשורטטים כמעברי חום סגוליים. השטח מתחת ל-
מאחר והמשאבה אידיאלית, אין בה אי-הפיכויות כלשהן. לכן נוכל לחשב את ההספק שלה,
מאיפה הדבר הזה נובע?
נביט בחוק ראשון עבור תהליך מתמיד עם כניסה ויציאה אחת:
אם מזניחים את השינויים באנרגיה פוטנציאלית וקינטית, ומניחים שאנו בתהליך הפיך פנימית, נקבל:
נזכור ממשוואות אנטרופיה ש:
נפעיל אינטגרל ונקבל:
נציב בחוק ראשון שפיתחנו ונמצא כי:
מאחר והמשאבה פועלת על נוזל דחוס, הנפח הסגולי של הנוזל לא משתנה, ולכן נוכל להניח ש-
דוגמה:
קיטור הוא הנוזל עבודה במחזור רנקין אידיאלי. אדים רוויים נכנסים לטורבינה ב-
ונוזל רווי יוצא מהמעבה בלחץ . סך ההספק שנוצר במחזור הוא . חשבו את היעילות.
פתרון:
נבנה סכמה של הבעיה:
נבנה דיאגרמתהמתארת את המחזור:
בכניסה הלחץ הואוהקיטור הוא אד רווי, אז מטבלאות קיטור נמצא כי: במצב
אנו יודעים כי , ומאחר ו- הוא תהליך איזנטרופי, נוכל למצוא מאינטרפולציה ש: האנתלפיה:
במצב
הנוזל רווי ב- , אז: במצב
האנטרופיה מקיימת . נוכל למצוא את ע”י אינטרפולציה בטבלת נוזל דחוס. אבל, מאחר ואין הרבה נקודות דגימה בטבלה זו, עדיף לנו להשתמש בנוסחה שפיתחנו עבור משאבה אידיאלית: נציב מטבלאות קיטור עבור מצב
ונקבל: סך ההספק שמתבצע הוא:
נוכל להציב בהגדרה ליעילות:
שיפור ביצועים
המחזורי עבודה שהצגנו כאן לא מתארים בצורה כל כך טובה תחנות כוח אמיתיים. ישנם מספר שיפורים שכיום משתמשים בהם כדי לקבל ביצועים יותר טובים.
נתחיל בלשים לב שהעלאת הלחץ בדוד או הורדת הלחץ במעבה תוביל לירידה באיכות האד ביציאה מהטורבינה. נוכל לראות זאת על דיאגרמת
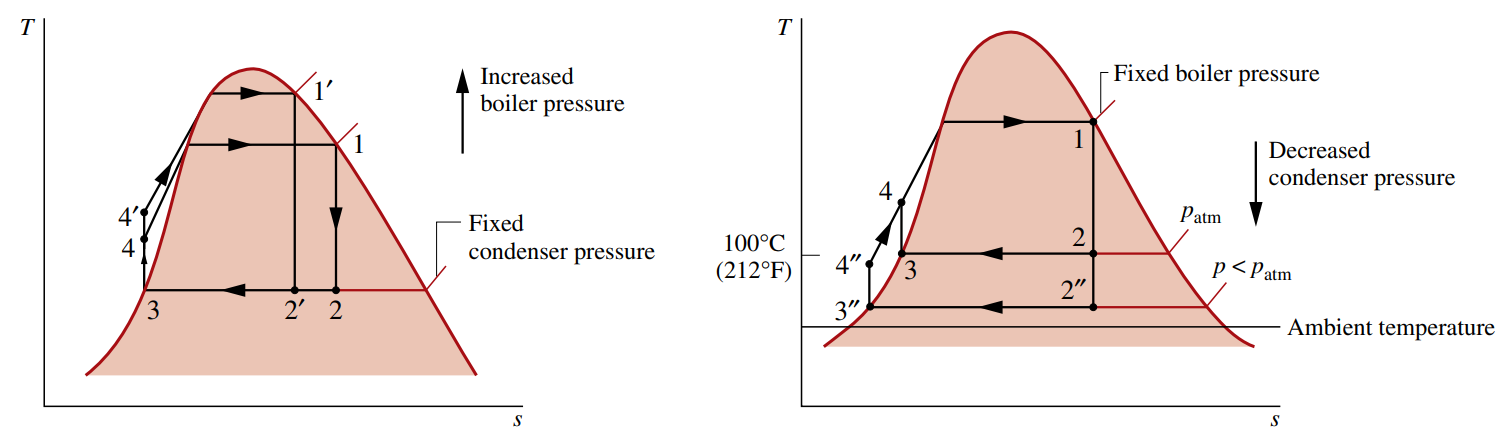
אם איכות האד של הקיטור העובר דרך הטורבינה נמוכה מדי, ייווצרו טיפות מים בזרימה וייפגעו פיזית בטורבינה - הם יישחקו (erode) את הלהבות שלה, ובכך יורידו את יעילות הטורבינה ויעלו את הדרישה לתחזוקה.
שיפורים כמו חימום ביניים מאפשרים ביצועים יותר טובים עם הפרשי לחצים יותר טובים בדוד ובמעבה, בלי לגרום לבעיה הזאת להיווצר.
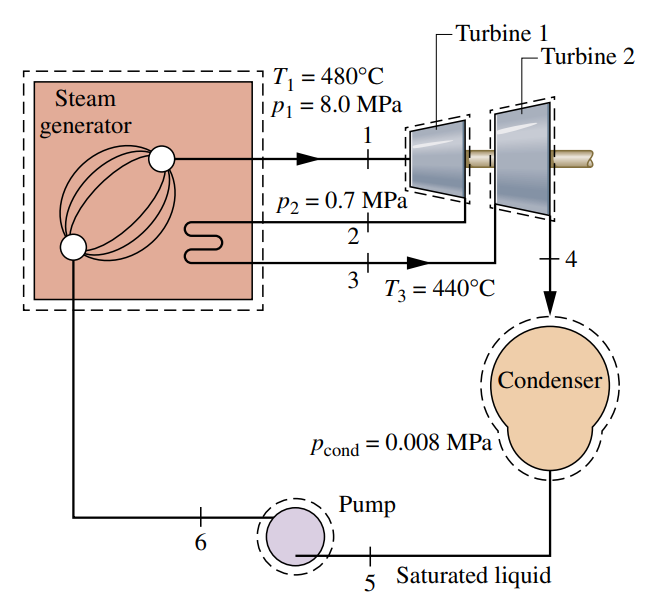
מחזור רנקין עם חימום ביניים
בחימום ביניים, תחנת כוח יכולה לנצל את העלאת היעילות כתוצאה מלחץ גבוה בדוד, מבלי ליצור איכות אד נמוכה ביציאה מהטורבינה:
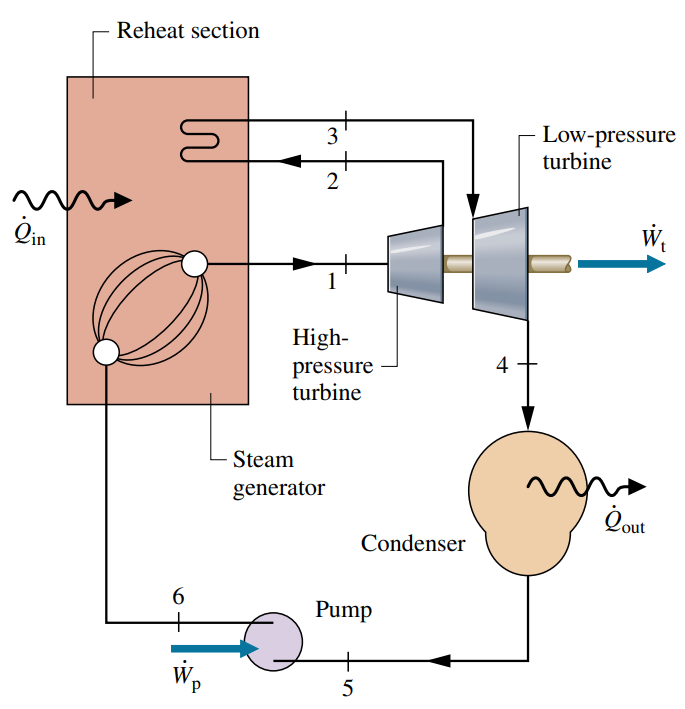
במחזור האידיאלי הנ”ל, קיטור לא מתפשט אל לחץ המעבה בשלב יחיד. במקום זאת, קיטור מתפשט דרך טורבינה (תהליך
הקיטור שיוצא מהטורבינה מחומם שוב בדוד (תהליך
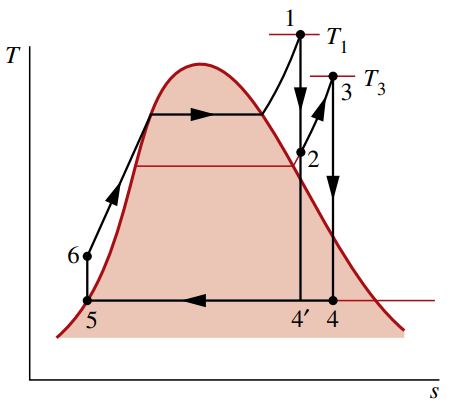
בכך אנו יכולים לנצל לחץ יותר גבוה בדוד, מבלי לקבל איכות אד נמוכה מדי בטורבינה.
דוגמה:
קיטור הוא הנוזל עבודה במחזור רנקין אידיאלי עם חימום ביניים. אדים רוויים נכנסים לטורבינה הראשונה ב-
ו- ומתפשטים ל- . לאחר מכן הוא מחומם שוב ל- לפני שהוא נכנס לטורבינה השנייה, בו הוא מתפשט ללחץ המעבה ב- . סך ההספק שנוצר במחזור הוא . חשבו את היעילות.
פתרון:
נבנה סכמה של הבעיה:
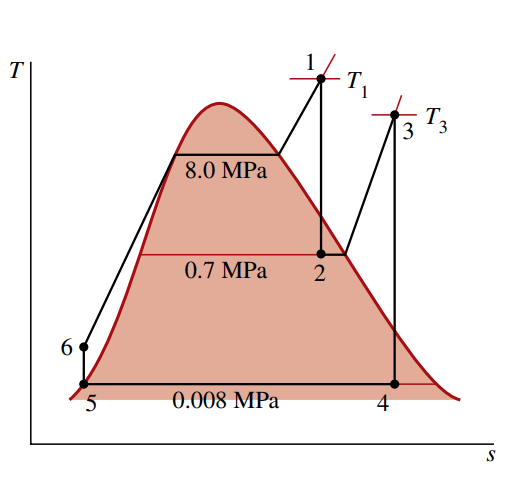
נבנה דיאגרמתהמתארת את המחזור:
בכניסה הלחץ הואוהטמפרטורה היא , אז מטבלאות קיטור נמצא כי: במצב
אנו יודעים ש- ו- כי ההפשטות היא התפשטות איזנטרופית. מטבלאות קיטור: לכן האנתלפיה:
במצב
עדיין ומתקיים . מטבלאות קיטור: במצב
יש ו- . נמצא מהטבלאות קיטור: האנתלפיה היא:
מצב
הוא נוזל רווי ב- , אז: לבסוף, המצב ביציאה מהמשאבה זהה לדוגמה הקודמת, אז:
סך ההספק שנוצר ע”י המחזור נתון ע”י:
באותו אופן כמו הנוסחאות שפיתחנו ממקודם, נסיק כי:
קצב האינטראקציית חום אל הנוזל עבודה (הקיטור) כאשר הוא עובר בדוד וחימום ביניים:
נוכל כעת לחשב את היעילות:
נשים לב כי קיבלנו יעילות יותר גבוה מהמחזור בדוגמה הקודמת. עבור הספק מסוים (
), יעילות יותר גבוה מעידה על קצב זרימת קיטור יותר נמוכה. מעבר לכך, עם יעילות יותר גבוה, קצב האינטראקציית חום למי הקירור גם כן קטן, ובכך אנו מקטינים את הדרישה למי קירור. בנוסף, עם החימום ביניים, איכות האד ביציאה מהטורבינה יותר גבוה מאשר בדוגמה הקודמת.
מחזור רנקין עם הקזה
שיפור נוסף למחזור רנקין נקרא מחזור רנקין עם הקזה.
ראינו במחזור רנקין אידיאלי, במחזור
כדי להעלות את הטמפרטורה של מצב
מחמם מי הזנה פתוח
במחזור רנקין עם מחמם מי הזנה פתוח, שני הזרמים - הקיטור המוקז והמים מהמעבה מתערבבים, ויוצרים זרם בטמפרטורה ממוצעת של שניהם.
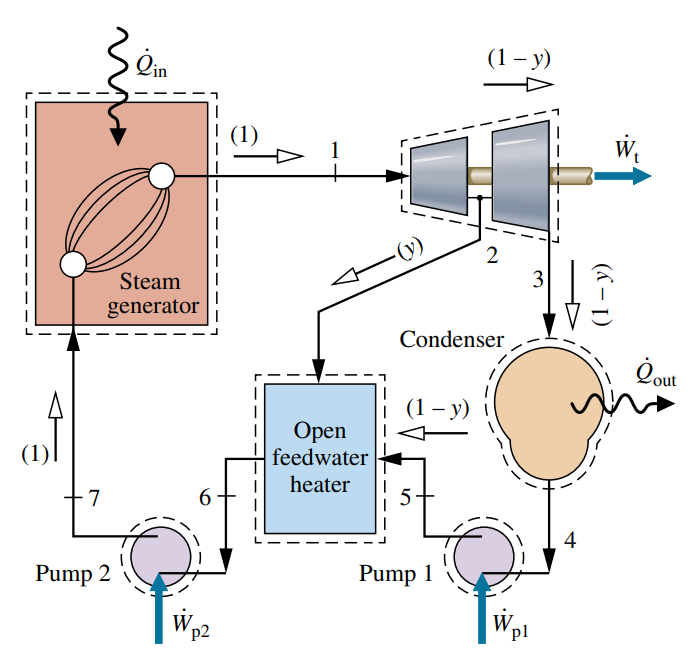
הדיאגרמת
במחזור זה, הקיטור עובר איזנטרופית דרך הטורבינות והמשאבות (כי אנחנו מניחים שהם אידיאליים), והזרם דרך הדוד, המעבה, ומחמם מי ההזזה מתרחשים ללא נפילה בלחץ. בכל זאת, ישנה אי הפיכות בערבוב במחמם מי הזנה.
קיטור יוצא מהטורבינה הראשונה במצב
בדיאגרמה מופיע מצב
כדי לחשב את נצילות המחזור, נצטרך לחקור כל שלב במחזור, כאשר נשים לב שכעת ישנם מחזורים בהם אין לנו את אותה הספיקה הכללית
כאשר נבחר נפח בקרה המכיל את שני הטורבינות, משימור המסה בתהליך מתמיד:
כאשר
כאשר נחלק ב-
נסמן את היחס בין הספיקה שיוצאת במצב
לכן:
היחס
מאחר ו-
דוגמה:
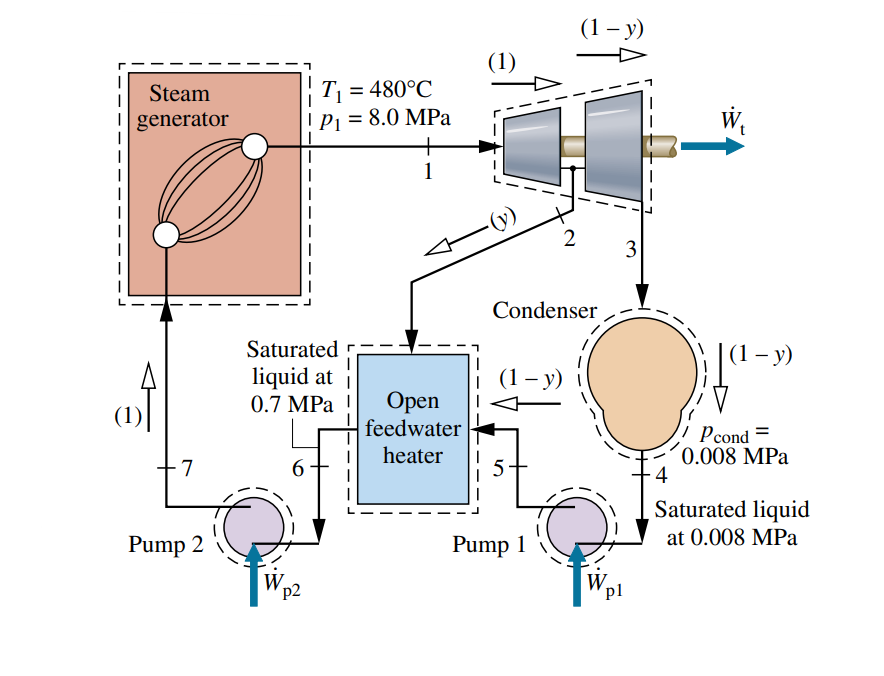
נחזור למערכת שכבר ראינו בדוגמה הראשונה, כאשר נוסיף מחמם מי הזנה:
נתון מחזור רנקין עם הקזה עם מחמם מי הזנה פתוח. קיטור נכנס לטורבינה ב-, ו- , ומתפשטת ל- , בו חלק מהקיטור מוקז למחמם מי הזנה בו הלחץ .
שאר הקיטור מתפשט דרך הטורבינה השנייה למעבה שהלחץ שלו הוא. נוזל רווי יוצא מהמחמם מי הזנה ב- . היעילות האיזנטרופית של כל טורבינה היא , וכל משאבה פועלת באופן איזנטרופי.
אם סך הספק המחזור הוא, מצאו את היעילות של המחזור ואת הספיקה שנכנסת לטורבינה הראשונה.
פתרון:
סכמת המחזור:
נבנה דיאגרמת:
האנתלפיות במצביםניתנים למציאה מטבלאות קיטור. האנתלפיה במצב כבר נמצאה בדוגמה קודמת, ובכך נוכל למצוא את האנטרופיה במצב זה. לסיכום: האנתלפיה במצב
ניתנת לחישוב מהיעילות הנתונה על הטורבינה השנייה: מאחר ו-
, איכות האד במצב היא . מכך, נסיק כי: מצב
הוא נוזל רווי ב- . לכן .
מאחר והמשאבות פועלות באופן איזנטרופי, האנתלפיה במצביםניתנים לחישוב בעזרת הנוסחה למשאבה אידיאלית: נסיק כי היחס
הוא: סך ההספק של הטורבינות:
סך העבודה שמתבצעת ע”י המשאבות:
החום שנכנס לדוד:
נסיק כי היעילות של המחזור היא:
ספיקת המסה של הקיטור הנכנס לטורבינה,
, ניתנת לחישוב בעזרת הערך הנתון עבור ההספק - . מאחר ו: ומתקיים:
נסיק כי:
מחמם מי הזנה סגור
ניתן לחמם את מי ההזנה גם בעזרת מתקן הנקרא מחמם מי הזנה סגור, שהוא סוג של מחליף חום בו הזרמים לא מתערבבים. מתקנים אלו הם מכלים סגורים בהם טמפרטורות מי ההזנה עולה ככל שהקיטור המוקז מעובה על הצד החיצוני של צינורות המכילים את מי ההזנה. מאחר ושני הזרמים לא מתערבבים, הם יכולים להיות בלחצים שונים.
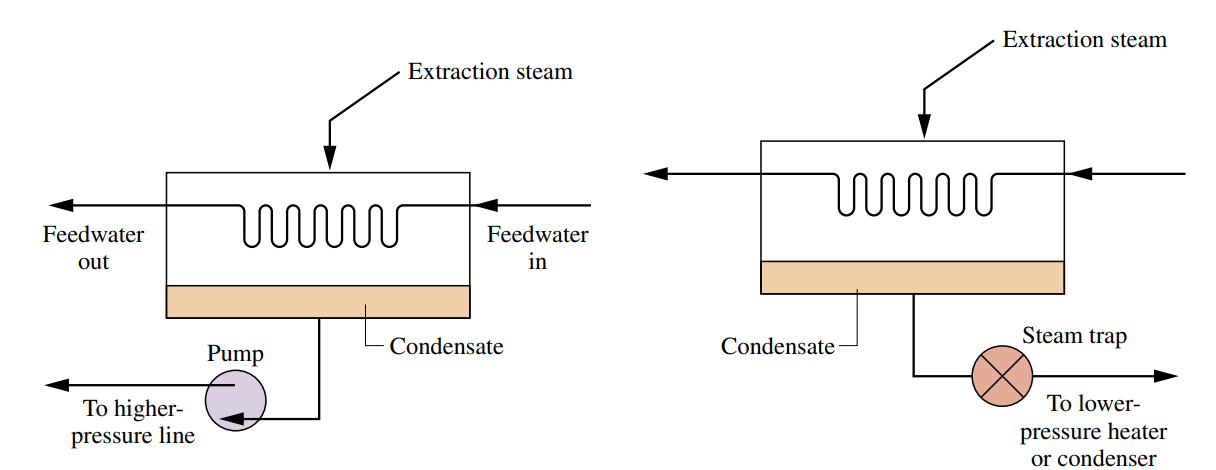
שתי דוגמאות למחממי מי הזנה סגורים.
במחזורים שנעסוק בהם לרוב נראה מחממי מי הזנה מהסוג הימני באיור - כאלה שביציאה ישנו שסתום, כך שהלחץ ביציאה יקטן כדי לא להעלות יותר מדי את הלחץ במעבה, אליו הקיטור המוקז חוזר.
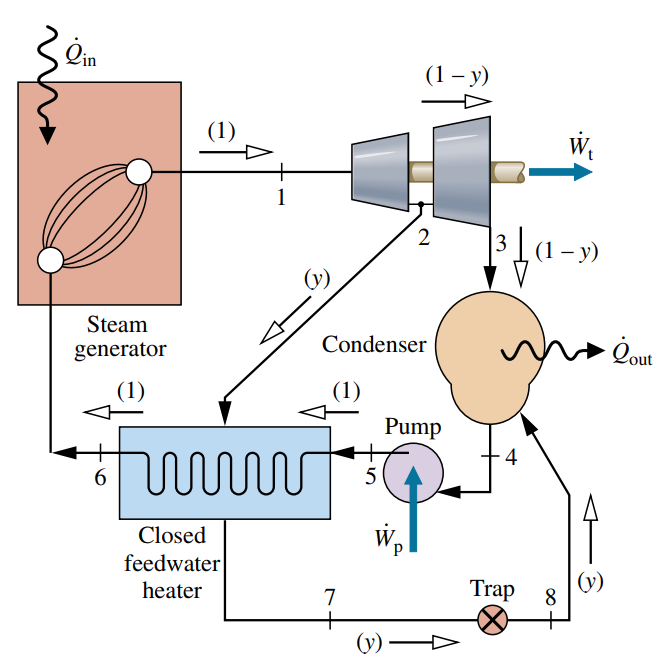
הדיאגרמת
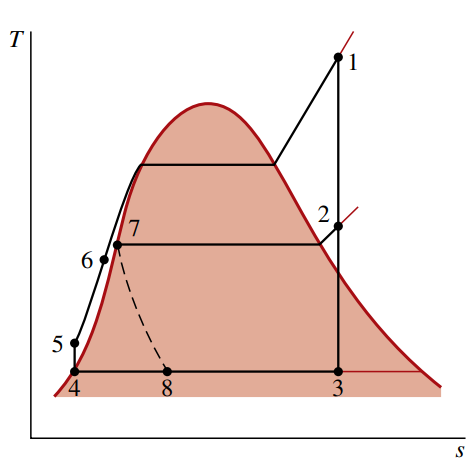
באותו אופן כמו במחמם מי הזנה פתוח, נוכל לפתח נוסחה עבור
תרגיל:
במחזור רנקין עם חימום ביניים, נכנס הקיטור לטורבינת לחץ גבוה ב-
סכמה של המחזור רנקין בבעיה.
- חשב את נצילות המחזור.
- חשב את הספיקה המסית של הקיטור.
- צייר את המחזור על דיאגרמת
. - חשב את נצילות קרנו למחזור עם טמפרטורה מינימלית ומקסימלית זהות.
פתרון:
-
נעבור חלק חלק, נבחר אותו כמערכת ונחשב עבורו חוק ראשון, על מנת לחשב את האנתלפיה בכל מצב. באותו אופן כמו בדוגמאות, אנו נמצא כי מהנתונים:
עתה יש לנו את הערכים בכל התחנות ונוכל לחשב את נצילות:
עתה נעשה חוק
על הטורבינות והמדחס: חוק ראשון על הבוילר:
נציב ביעילות ונקבל:
-
הספיקה המסית ניתנת לחישוב ע”י:
-
דיאגרמת
:
הדיאגרמת
עבור המחזור המתואר.
- נצילות קרנו: