THE1_005 החוק השני של התרמודינמיקה

מוטיבציה לחוק השני

ביום יום אנו חווים תופעות בעלות כיווניות מסוימת. למשל, ניקח את שלושת המקרים הכלליים הבאים:

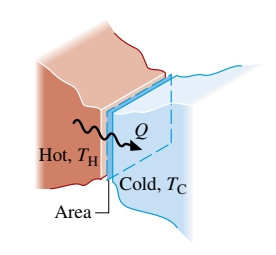
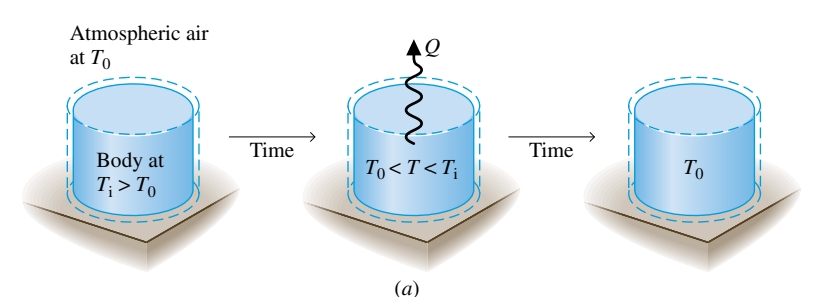
1. מערכת - חפץ בטמפרטורה גבוהה מונח במגע עם האטמוספירה בטמרפטורה , ובסוף מתקרר לטמפרטורה של סביבתו. בהתאם לחוק שימור האנרגיה, הירידה באנרגיה הפנימית של הגוף הופכת לעליה באנרגיה הפנימית של הסביבה. התהליך ההפוך לא יכל לקרות בספונטניות, למרות שגם בתהליך זה יתקיים חוק שימור האנרגיה.
   
2. מערכת - אוויר בלחץ גבוה נמצא במיכל סגור זורם לסביבה בעלת הלחץ היותר נמוך ב- כאשר פותחים את השסתום המחובר בינהם. לבסוף, הזרימה מפסיקה כאשר הלחצים השתוו. התהליך ההפוך לא יקרה, למרות שחוק השימור האנרגיה עדיין יתקיים בתהליך זה.
   
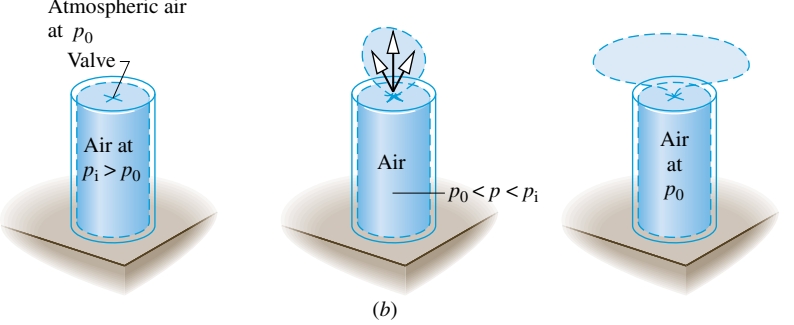
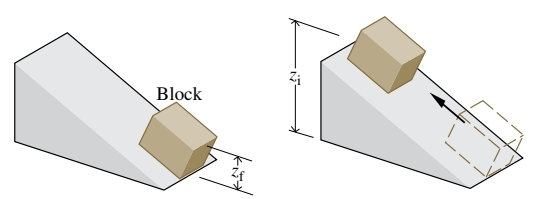
3. מסה התלויה על כבל בגובה נופלת כאשר היא משוחררת. כאשר היא מגיעה לעצירה, האנרגיה הפוטנציאלית של המסה מהמצב ההתחלתי שלה מופיעה כתוספת לאנרגיה הפנימית של המסה וסביבתה, בהתאם לחוק שימור האנרגיה. התהליך ההפוך לא יקרה ספונטנית, למרות שהאנרגיה תישמר בתהליך זה. המסה לא ספונטנית תעלה בחזרה לגובה הקודם שלה.
   

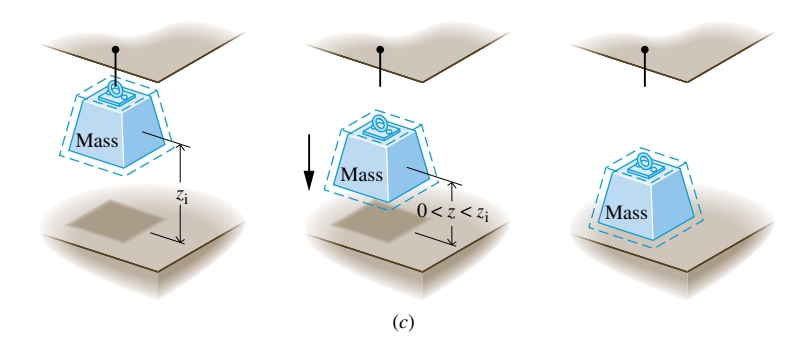
נסיק מהמקרים הללו שלא כל תהליך שמקיים את חוק שימור האנרגיה יתקיים. בכללי, שימור אנרגיה לבדו לא יגלה לנו מה הכיוון שתהליך מסוים ייקח, או אפילו הוא לא יבדיל את התהליך שיקרה מהשאר.
במקרים שתוארו אנו יודעים באיזה כיוון התהליך יקרו כי הם מקרים נפוצים שקורים ביום יום שלנו. אבל למקרים יותר מסובכים, שבו הניסיון שלנו לא מספיק, נרצה איזשהו חוק שידריך אותנו.

נוסחים של החוק השני

נדבר על שני נוסחים שונים של החוק השני:

1. קלאוזיוס (ההוא של הקלאוזיוס-קלפירון).
2. קלוין-פלאנק (ההוא של הטמפרטורה וההוא של ההתאוריה הקוונטית).

נוסח קלאוזיוס

נוסח קלאוזיוס של החוק שני קובע כי:

משפט:

זבלתי אפשרי למערכת לפעול כך שהתוצאה היחידה של הפעולה שלה הוא מעבר חום מגוף קר לגוף חם.

נוסח קלאוזיוס לא אוסרת את האפשרות של מעבר חום מגוף קר לגוף חם - הרי זה מה מקררים ומשאבות חום מבצעות. הטענה במילים “תוצאה יחידה” היא שחייבים להיות תוצרים אחרים בתוך המערכת שגורמים למעבר חום.

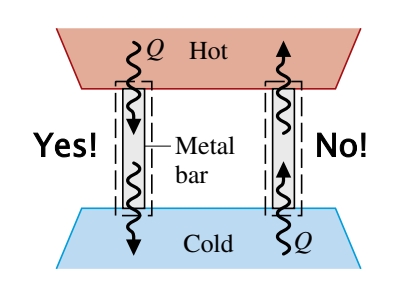
דוגמה:

קירור אוכל לרוב מתבצע ע”י מקררים שפועלים על הספק חשמלי. נוסח קלאוזיוס טוען שאי אפשר לבנות מקרר שפועל ללא הספק כשלהו.

נוסח קלוין-פלאנק

משפט:

בלתי אפשרי למערכת כלשהי לעבוד במחזור תרמודינמי ולהעביר אנרגיה ע”י עבודה לסביבתה בזמן שהיא קולטת אנרגיה ע”י חום ממאגר חום יחיד.

נוסח קלוין-פלאנק לא אוסר על האפשרות שמערכת תיצור עבודה ממעבר חום שהגיע ממאגר חום כלשהו. היא רק אוסרת על האפשרות הזאת אם המערכת עוברת מחזור תרמודינמי.

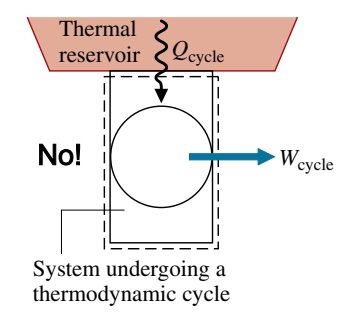
נוכל להציג את הנוסח הזה בצורה אנליטית:
נניח את התנאים על המערכת לפי הנוסח. מאחר והמערכת עוברת מחזור:

במילים, העבודה שמתבצעת על (או ע”י) המערכת העוברת מחזור שווה למעבר החום מהמערכת (או אל המערכת). בעוד מאזן אנרגיות זה אמנם מאפשר ל- להיות חיובי או שלילי, החוק השני מציב מגבלה על .
לפי נוסח קלוין-פלאנק, מערכת במחזור ושבמגע תרמי עם מאגר חום לא יכולה להעביר עבודה לסביבתה. כלומר, העבודה במחזור לא יכולה להיות חיובית. נשים לב שעדיין יכל להיות מעבר אנרגיה למערכת בצורת עבודה בזמן המחזור, או שכלל העבודה היא אפסית. כלומר, לפי נוסח קלוין-פלאנק:

שני הנוסחים שקולים אחד לשני

ניתן להראות ששני הנוסחים, נוסח קלאוזיוס ונוסח קלוין-פלאנק, שקולים אחד לשני. נוכל לעשות זאת ע”י הוכחה שמראה כי אם הפרנו את אחד מהנוסחים, אז נפר גם את הנוסח האחר.
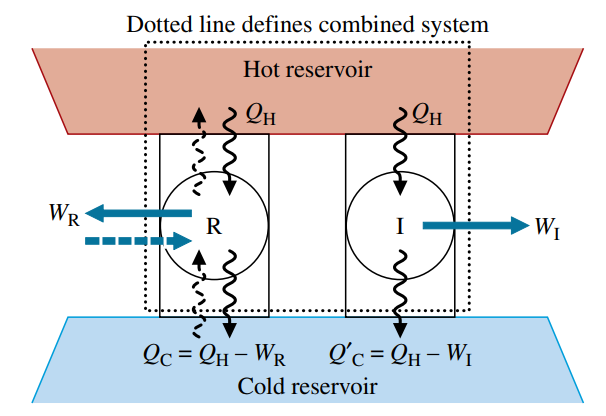
נביט באיור הבא:

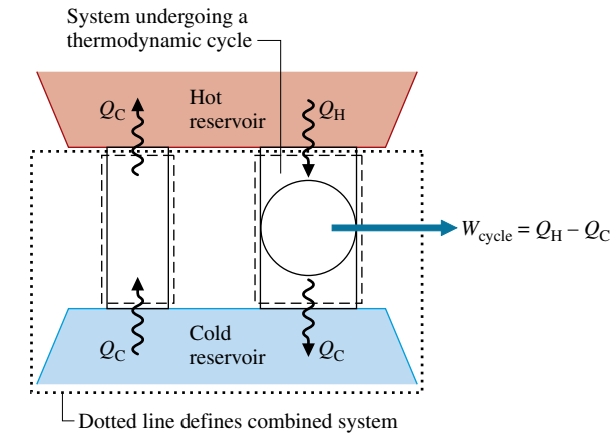
המערכת בצד שמאל מעבירה חום מהמאגר הקר למאגר החם ללא שום אפקטים/תוצרים אחרים, ובכך מפרה את נוסח קלאוזיוס.
המערכת מימין פועלת במחזור כאשר היא מקבלת (גדול יותר מ-) מהמאגר החם, פולטת למאגר הקר, ומפעילה עבודה לסביבתה.

נביט במערכת הכוללת כפי שמוצג באיור ע”י המלבן הגדול המקווקו. מערכת זו כללת את המאגר הקר ושתי המערכות הקודמות. מערכת כוללת זו פועלת במחזור כי חלק אחד שלה פועל במחזור ומצב שני החלקים האחרים לא משתנה. בנוסף, המערכת הכוללת מקבלת אנרגיה במעבר חום ממאגר חום אחד - המאגר החם, ומבצעת עבודה באותו הגודל - גודל שהוא חיובי. לפיכך, המערכת הכוללת מפרה את נוסח קלוין-פלאנק.

באותו אופן, נוכל להוכיח שהפרה של נוסח קלוין-פלאנק תוביל להפרה של נוסח קלאוזיוס.

תהליכים הפיכים ובלתי הפיכים

אחד מהשימושים החשובים של החוק השני של התרמודינמיקה בהנדסה הוא לחשב את הביצועים התאורתיים הכי טובים של מערכות שונות.
כאשר נשווה בין הביצוע התאורתי לביצוע המעשי, נוכל להבחין בדרכים לשפר את המערכת הקיימת. נראה שהביצועים הכי טובים מתרחשים בתהליכים אידאליים, שאלו הם תהליכים שניתנים להפיכה.

תהליך הפיך

הגדרה:

נאמר כי תהליך נקרא תהליך הפיך אם המערכת וסביבתה יכולים לחזור בדיוק למצבם ההתחלתי.
באותו אופן, תהליך נקרא בלתי הפיך אם המערכת וסביבתה לא יכולים לחזור בדיוק למצבם ההתחלתי.

נשים לב שמערכת שעברה תהליך בלתי הפיך תוכל לחזור למצבה ההתחלתי. אבל, אם היא אכן תחזור למצבה המקורי, לא נוכל להחזיר את הסביבה למצבה המקורי.

דוגמה:

רוב התהליכים שאנו מכירים הינם תהליכים בלתי הפיכים:

1. מעבר חום בין הפרש טמפרטורות סופי.
   
2. תגובה כימית ספונטנית.
3. דפורמציה פלסטית.
4. חיכוך.
   
5. זרם חשמלי דרך נגד.

נוכל לנחש, ולנחש נכון, שלמעשה כל התהליך המציאותיים הם בלתי הפיכים. לכן, הרעיון של תהליך הפיך הוא היפוטתי לחלוטין, כי הוא בעצם תהליך שהתבצע בצורה מושלמת. למרות זאת, עדיין ישנם תהליכים שמאוד מתקרבים להיות הפיכים, או לפחות כאלה שנוכל לדמיין. למשל, הנה שני דוגמאות קלאסיות:

1. מטוטלת בריק. התנועה של המטוטלת שואפת לאי הפיכות ככל שהחיכוך בציר קטן. כאשר באמת אין חיכוך, גם המטוטלת וגם הסביבה יחזרו למצבם המקורי בסוף כל מחזור.
   
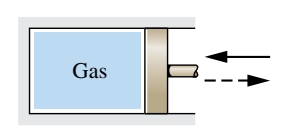
2. מערכת המכילה גז נדחסת ומתפשטת אדיאבטית בבוכנה חסרת חיכוך. עם שינויים מאוד קטנים בלחץ החיצוני, הבוכנה תידחוס את הגז מאוד לאט. בכל שלב ביניים במהלך הדחיסה, התכונות האינטנסיביות וכו’ יהיו אחידים בכל המערכת. באותו אופן בהתפשטות.
   זהו תהליך קוואזיסטטי, פעם בדחיסה ופעם בהתפשטות. העבודה שהתבצעה על הגז בזמן הדחיסה תהיה שווה לעבודה שהתבצעה ע”י הגז בזמן ההתשפטות. כלומר, אין שינוי בסביבה שלנו או במערכת עצמה. לכן תהליך זה הפיך.
   

הערה:

תהליך קוואזיסטטי הוא לא תמיד הפיך!

תהליך הפיך פנימית

הגדרה:

תהליך הפיך פנימית הוא תהליך שניתן להחליפו לתהליך הפיך ע”י שינויים בסביבה, כאשר המערכת עצמה לא משתנה.
עוד הגדרה שקולה היא שתהליך הפיך פנימית הוא תהליך שבו אין תהליכים בלתי הפיכים בתוך המערכת. בסביבה, עדיין יכולים להתרחש תהליכים בלתי הפיכים.

דוגמה:

נחשוב על מים שמתעבים בחזרה לנוזל בטמפרטורה של בזמן שהם זורמים דרך צינור נחושת קר (). המים עוברים תהליך הפיך פנימי, אבל ישנו מעבר חום מהמים לצינור.
עבור הנפח בקרה שתוחם את המים בתוך הצינור, המעבר חום הוא תהליך בלתי הפיך חיצוני.

בכל מצב ביניים של תהליך הפיך פנימית במערכת סגורה, כל התכונות האינטנסיביות אחידות. אם יש אי אחידות למשל בטמפרטורה באחד מהאזורים במערכת, יהיה נטייה למעבר ספונטני של אנרגיה בתוך המערכת ואז התהליך לא היה הפיך.
נסיק כי תהליך הפיך פנימית הוא תהליך שבכל שלב ביניים ישנו ש”מ - זהו תהליך קוואזיסטטי.

הערה:

תהליך הפיך פנימית הוא תהליך קוואזיסטטי וגם ההפך הוא נכון. בהמשך נשתמש בשתי השמות האלו לסירוגין.
שוב, תהליך הפיך הוא בהכרח קוואזיסטטי, אבל תהליך קווזאיסטטי הוא לא בהכרח הפיך. הוא כן הפיך פנימית.

פירוש נוסח קלוין-פלאנק

ראינו כי לפי נוסח קלוין-פלאנק, עבור מערכת הנמצאת במגע תרמי עם מאגר חום יחיד ובמחזור:

נביט במערכת מסוג זה:

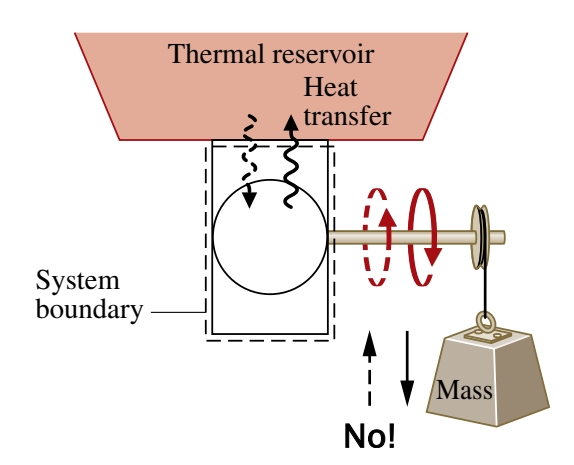
העבודה מועברת ל-(או נקלטת מ-) המערכת גלגלות בסביבה. נניח כי המאגר חום והגלגלות מבצעות תהליכים הפיכים.
אם העבודה במחזור היא אפסית ():

• המערכת בוודאות תחזור למצבה המקורי.
• מאחר ו-, לא יהיה שינוי בגובה המסה שנמצאת בסביבה.
• מאחר ו-, נסיק כי גם , אז גם אין שינוי במאגר חום.

לכן, המערכת וכלל הסביבה שלה יחזרו בדיוק למצבם המקורי. בהגדרה, התהליך שהתבצע הוא הפיך. נוכל להוכיח גם בצורה ההפוכה שאם תהליך הוא הפיך, אז .

לפיכך, האי שוויון יתרחש כאשר ישנם תהליכים בלתי הפיכים פנימית. במילים, סך העבודה שהתבצעה על המערכת למחזור מומרת ע”י תהליכים בלתי הפיכים פנימית, לאנרגיה פנימית שנפלטת במעבר חום למאגר חום בכמות השווה לסך העבודה.

נסיק כי:

חוק שני במכונות חום

גבול הנצילות

נוכל למצוא גבול עליון לנצילות של מכונת חום בעזרת נוסח קלוין-פלאנק. נביט באיור הבא:

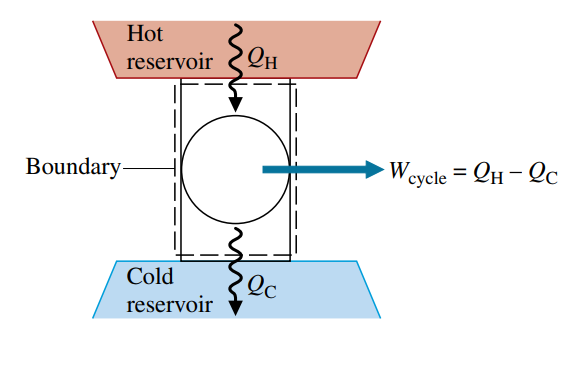
המערכת הנתונה נמצאת במחזור ובמגע עם שני מאגרי חום - אחד חם ואחד קר, כאשר היא מבצעת עבודה . הנצילות של מנוע חום זה הוא:

הערה:

המעברי אנרגיה המסומנים באיור חיוביים בכיוון החץ.

אם הערך של הוא אפס, המערכת תקלוט אנרגיה מהמאגר החם ותבצע עבודה שווה ל-. הנצילות במקרה זה הוא . אבל, תהליך זה נוגד את נוסח קלוין-פלאנק, כי אז הוא יהיה שקול מערכת במגע תרמי עם מאגר חום יחיד בעל עבודה חיובית.

נסיק כי בכל מכונת חום הפועלת בין שני מאגרי חום, רק חלק מהאנרגיה של יכולה להפוך לעבודה, והשארית כ-. לכן, הנצילות המקסימלית קטנה יותר מ-, גם אם התהליך שמתבצע הוא תהליך הפיך.

עקרונות קרנו

מאחר ושום מנוע חום לא יכל להיות עם נצילות של נרצה לדעת מהי הנצילות המקסימלית שנוכל להגיע אליה. באותו אופן נרצה לדעת לגבי המקדמי ביצוע של מקררים ומשאבות חום.
מנוע קרנו שנדבר עליו בהמשך הוא דוגמה למנוע בעל נצילות מקסימלית, והוא לוקח בחשבון את שני העקרונות הבאים:

1. הנצילות של מנוע חום בתהליך בלתי הפיך תמיד תהיה נמוכה מהנצילות של מנוע חום בתהליך הפיך כאשר כל אחד מהם פועל בין שני מאגרי חום.
2. כל מנועי החום הפועלים בתהליך הפיך בין אותם שני מאגרי חום, בעלי אותה הנצילות.

הוכחה?

נוכל להדגים את העיקרון הראשון בעזרת המצב המתואר באיור הבא:

מנוע חום בתהליך הפיך ומנוע חום בתהליך בלתי הפיך פעולים בין אותם שני המאגרי חום ומקבלים את אותו החום מהמאגר החם.
התהליך ההפיך יוצר עבודה , ואלו התהליך הבלתי הפיך יוצר עבודה . לפי חוק ראשון, כל מחזור פולט אנרגיה למאגר הקר ככמות ההפרש בין והעבודה שנוצרה.

עכשיו, נהפוך את הכיוון שבו המנוע החום עובד, כך שהוא הופך למקרר (או משאבת חום). מאחר ו- מבצע תהליך הפיך, הגדלים של , , ו- נשארים אותו הדבר, אבל המעברי אנרגיה משנים את כיוונם. כעת, במצב זה, המאגר החם לא מרגיש שינוי במצבו בתחילת כל מחזור, מאחר וה- שהוא מקבל מ- מועבר ל-.

נוכל לראות את העיקרון הראשון של קרנו כאשר ניקח בחשבון את המערכת הכוללת המסומנת באיור. מאחר וחלקיה לא משתנים כל מחזור, המערכת הכוללת נמצאת במחזור בפני עצמה. בנוסף, המערכת הכוללת נמצאת במגע עם מאגר חום יחיד - המאגר הקר. לפי פירוש נוסח קלוין-פלאנק, העבודה של המערכת הכוללת במחזור היא:

כאשר ישנו אי שוויון כי ישנם תהליכים בלתי הפיכים בתוכה (בתת-מערכת ).

מאחר והעבודה הכוללת היא סכום העבודות של כל חלקי המערכת:

לפי נצילות מנוע, נסיק כי:

סקאלת קלוין

הנצילות והביצועים המקסימליים של מכונות חום ניתנים לחישוב בעזרת סקאלת קלוין. עבור העיקרון השני של קרנו אנו יודעים שכל מנוע חום בתהליך הפיך הפועל בין שני מאגרי חום הוא בעל אותו הנצילות.
לפיכך, הנצילות תלויה רק במאגרי חום עצמם, כלומר בהפרש טמפרטורות שלהם. לפי גבול הנצילות:

כאשר הם הטמפרטורות של המאגרי חום, והפונקציה היא כרגע לא ידועה. נשים לב שמשוואה זו נכונה רק עבור מכונות חום בתהליך הפיך שבאות במגע עם שני מאגרי חום (ולכן הסימון ).

משוואה זו מהווה בסיס להגדרת סקאלת טמפרטורה תרמודינמית - סקאלה שלא תלויה בתכונות של שום חומר. ישנם מספר אפשרויות שונות ל-, אבל אנו נתעסק בסקאלת קלוין, שניתנת כאשר אנו מחליטים ש :

משוואה זו נותנת לנו רק יחס. נצטרך להגדיר עוד נתון על הסקאלה כדי להשלים את ההגדרה של הסקאלה. הוסכם להגדיר ש- היא הטמפרטורה של הנקודה המשולשת של מים. לפיכך, אם תהליך הפיך מתבצע בין מאגר חום ב- למאגר חום בטמרפטורה , אז היחס בין שני הטמפרטורות הוא:

מאחר ולפי עיקרון קרנו השני הנצילות של התהליך ההפיך לא תלויה במבנה המערכת, ההגדרה של הטמפרטורה במשוואה זו אכן לא תלויה בתכונות של שום חומר.

נצילות ומקדמי ביצוע מקסימליים

כעת, נוכל להציב את המשוואה מסקאלת קלוין בנצילות של מנוע חום כדי לקבל שעבור מנוע חום בתהליך הפיך, הפועל בין שני מאגרי חום בטמפרטורות ו-, מתקיים:

הידוע בשם נצילות קרנו.

באותו אופן, נוכל להסיק שהמקדמי ביצוע המקסימליים של מקררים ומשאבות חום בתהליך הפיך נתונים ע”י:

מנוע קרנו

מנועי קרנו (Carnot) הם דוגמאות לתהליכים הפיכים הפועלים בין שני מאגרי חום. לכן, הם יהיו בעלי נצילות מקסימלית.

הגדרה:

במנוע קרנו, המערכת המפעילה את המחזור עוברת 4 תהליכים הפיכים פנימית: 2 אדיאבטים ו-2 איזותרמים.

מחזור מנוע קרנו

הדיאגרמת הבאה מתארת את מחזור מנוע קרנו במערכת בה ישנו גז בבכנה היושבת בתוך צילינדר:

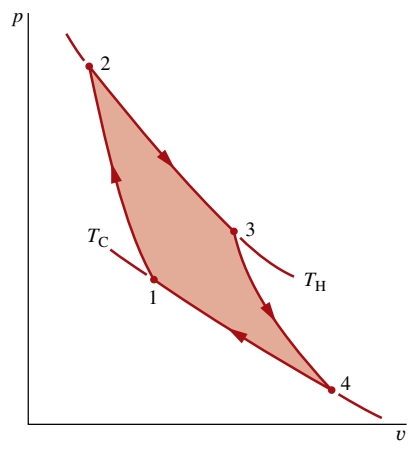
דיאגרמת המתארת מחזור קרנו.

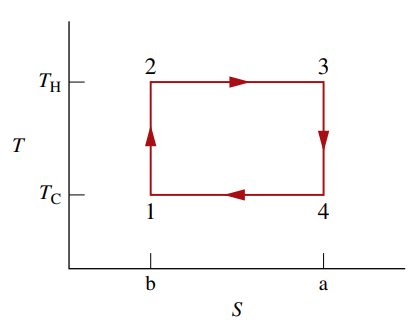
דיאגרמת של מחזור קרנו. ה- הוא אנטרופיה - תכונה שנלמד בהמשך.

באיור הבא מתארים איך מחזור כזה יכול להיראות:

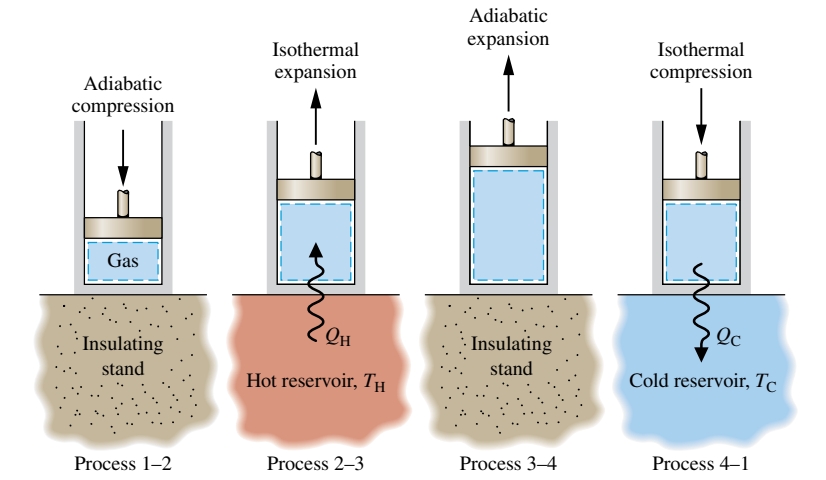
המעברי חום מתוארים בכיווני החצים.

• תהליך : הגז נדחס אדיאבטית למצב , בו הטמפרטורה היא .
• תהליך : הצילינדר מונח במגע עם מאגר חום בטמפרטורה . הגז מתפשט איזותרמית כאשר הוא קולט חום מהמאגר חום.
• תהליך : הצילינדר מונח שוב על משטח מבודד והגז ממשיך להתפשט אדיאבטית עד שהטמפרטורה יורד ל-.
• תהליך : הצילינדר מונח במגע עם מאגר חום בטמפרטורה . הגז נדחס איזותרמית עד שהוא מגיע למצבו ההתחלתי בזמן שהוא פולט אנרגיה למאגר חום.

לכל אחד מארבעת התהליכים ההפיכים פנימית של מחזור קרנו, העבודה ניתנת לייצוג כהשטח מתחת לגרף . השטח הכלוא בין כל ארבעת התהליכים הוא סך העבודה במחזור שמבצעת המערכת (ליחידת מסה).

---

תרגיל:

מנוע חום פועל בין שני מאגרים בטמפרטורות של ו-. כמויות החום המוחלפות במחזור הן ו-. קבעו האם מנוע חום זה הפיך, בלתי הפיך או בלתי אפשרי.

פתרון:
נחשב את הנצילות של המנוע חום:

הנצילות של מנוע קרנו הוא:

מאחר ו-, נקבל כי התהליך הנתון לא אפשרי.

---

תרגיל:
מכונת קירור פועלת בין מאגרי חום בטמפרטורת ו-. חלק מן העבודה הדרושה להפעלתה מתקבל ממנוע חום הפועל בין מאגרים בטמפרטורות ו-. היתר, מסופק ע”י מקור אחר. חום מסופיק למנוע מהמאגר בקצב של . חשב את קצב אינטראקציית החום המקסימלית המסולקת מהמאגר הקר.

פתרון:
קודם נביט במקרר עצמו. כאשר הוא הכי יעיל, אז הוא יוציא מקסימום חום מהמאגר קור. כעת, כדי לבצע כמה שיותר עבודה, נדרוש גם שהמנוע חום יעבוד בנצילות מקסימלית כדי לספק עבודה מקסימלית.

עבור המנוע חום, הנצילות המקסימלית:

ולכן ההספק המקסימלי:

לכן המקסימום עבודה שאנו יכולים להכניס לתהליך קירור שלנו הוא:

מקדם הביצועים המקסימלי של המקרר:

מאחר ומקדם הביצועים של המקרר נתון ע”י:

לכן, עבור ערכי ו- מקסימליים שחישבנו מקודם:

אי שווויון קלאוזיוס

עקרונות קרנו שעסקנו בהם עד בה הם עבורים מערכות במחזור שבאות במגע עם אחד או שני מאגרי חום. נוכל לרשום עיקרון יותר כללי, הנקרא אי שוויון קלאוזיוס, שתקף לכל מחזור ללא קשר למספר מאגרי החום. עיקרון זה קובע כי לכל מחזור תרמודינמי:

כאשר הוא המעבר חום של המערכת בקטע מסוים, ו- הוא הטמפרטורה (בקלוין) בגבול בו מתקיים מעבר החום. הסימון נועד כדי להדגיש כי האינטגרל מחושב לאורך כלל הגבול ולכל המחזור.

כמו בפירוש נוסח קלוין-פלאנק, השוויון מתקיים אם התהליך הוא הפיך, והאי שוויון כאשר התהליך הוא בלתי הפיך.