שאלה 1
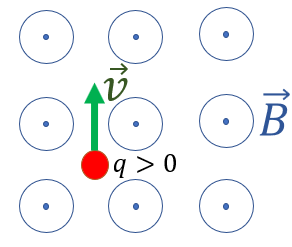
סכמת הבעיה
לפי הגדרת הכוח המגנטי:
ולכן כיוון הכוח יהיה ימינה.
שאלה 2
לפי דוגמה של כוח מגנטי על חלקיק בתנועה:
ולכן:
נציב נתונים ונקבל:
בנוסף, גם:
נציב נתונים:
שאלה 3
כמו בשאלה קודמת, נוכל להסיק כי:
ולכן:
שאלה 4
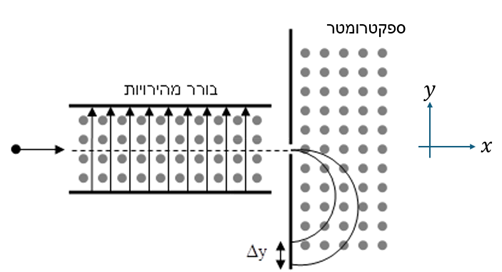
סכימת היונים והשדה המגנטי
נסמן את השדה המגנטי בספקטרומטר ב-
מדוגמה של כוח מגנטי על חלקיק בתנועה, אנו יודעים ש-
ולכן עבור כל אחד מהאיזוטופים:
ולכן הקטרים:
עלינו למצוא את
נסיק שלשני האיזוטופים אותה מהירות התחלתית. נציב בחיסור בין
נציב נתונים ונקבל ש:
שאלה 5
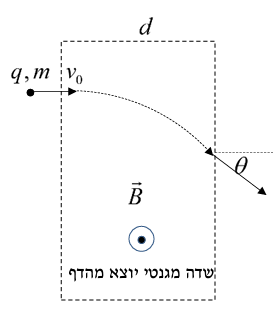
סכימת החלקיק והשדה המגנטי
מדוגמה על הכוח המגנטי, זמן המחזור הוא:
כלומר, ייקח לחלקיק
שאלה 6
מדוגמה על הכוח המגנטי, רדיוס הסיבוב מקיים:
סכימת הגליל והחלקיק
נדרוש ש-
ולכן:
שאלה 7
מאחר וזהו הכוח היחיד שפועל על החלקיק, נוכל להסיק שתאוצתו ההתחלתית (לפי חוק שני של ניוטון):
למעשה, כיוון ש-
כאשר
נשים לב שהיחיד מהתשובות בעל מבנה זה עבור
בדיקת שפיות זריזה גם מראה שאכן רדיוס הסיבוב בתנועה של חלקיק תחת השפעת שדה מגנטי היא:
שאלה 8
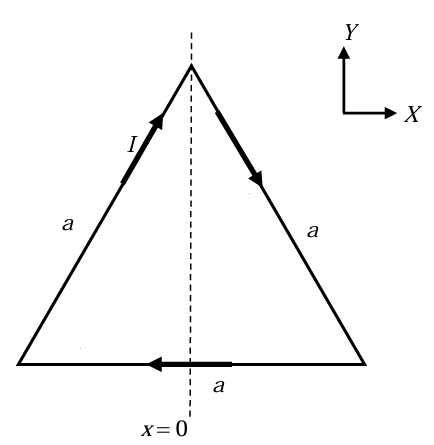
סכימת המשולש
מכוח מגנטי הפועל על זרם, ומהנתון, נסיק כי:
לכן:
שאלה 9
מדוגמאות על כוח מגנטי הפועל על זרם, נוכל לחשב פשוט את המרחק בין נקודת התחלה לנקודת סוף של התיל, ולבצע איתה מכפלה וקטורית על הזרם:
נוכל במקרה הזה לעשות זאת גם כאשר
שאלה 10
באותו אופן כמו שאלה קודמת:
מבחינת אורך מנקודת התחלה עד הסוף, תיל