PHY2_HW006 גיליון בית 6

שאלה 1

מפוטנציאל חשמלי של קליפה כדורית, וסופרפוזיציה של שתי קליפות כדוריות, נוכל להסיק כי הפרש הפוטנציאלים הוא:

נציב בהגדרת הקיבול ונקבל:

נקבל:

שאלה 2

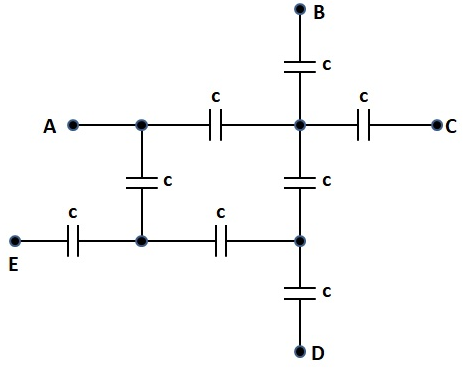
לאחר זיהוי של קבלים מחוברים בטור:

לאחר זיהוי של קבלים מחוברים במקביל:

נסיק שקיבול המערכת הוא .

שאלה 3

לאחר החיבור, הפוטנציאלים של שני הכדורים שווים:

נציב את ההגדרת הקיבול:

כאשר ו- הם המטענים על הכדורים לאחר החיבור.
אנו יודעים גם משימור מטען:

משתי המשוואות נקבל ש:

נציב בהגדרת הקיבול שוב כדי למצוא את הפוטנציאל על הכדור:

נציב נתונים ונקבל:

שאלה 4

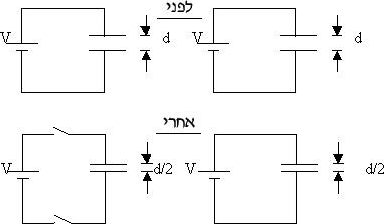
המעגלים החשמליים הנתונים

סעיף א’

מאנרגיה אגורה בקבל, לפני ואחרי הניתוק:

נחסר בין שתי המשוואות:

את הקבל השמאלי מנתקים לפני קירוב הלוחות, כך שכמות המטען בו נשארת אותה כמות המטען . בנוסף, מקבל לוחות, הקיבול נתון ע”י:

נציב בביטוי ל-:

נשים לב שגם , ולכן:

סעיף ב’

מאנרגיה אגורה בקבל, לפני ואחרי הניתוק:

נחסר בין שתי המשוואות:

את הקבל הימני משאירים מחובר למקור המתח, ולכן . בנוסף, מקבל לוחות, הקיבול נתון ע”י:

נציב בביטוי ל-:

נשים לב שגם , ולכן:

שאלה 5

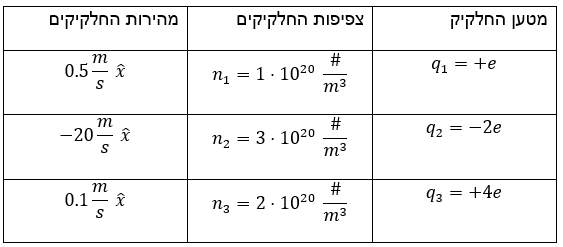
שלושת סוגי החלקיקים

מצפיפות זרם חשמלי:

נשים לב שכל שמהירויות כל המטענים הן בכיוון , ולכן נקבל פשוט:

נציב את הנתונים:

לכן:

שאלה 6

סעיף א’

לפי התנגדות וחוק אוהם:

נציב נתונים ונקבל:

סעיף ב’

לפי הספק חום מהתנגדות:

נציב נתונים:

שאלה 7

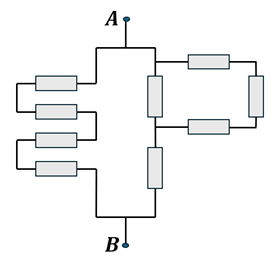
המעגל החשמלי הנתון

לאחר זיהוי של נגדים מחוברים בטור:

לאחר זיהוי של נגדים מחוברים במקביל:

לאחר זיהוי של נגדים מחוברים בטור:

ולכן ההתנגדות הכוללת:

שאלה 8

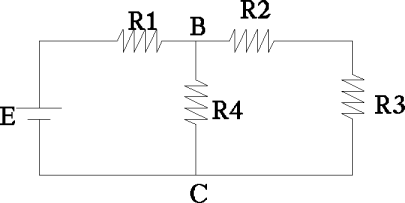
המעגל הנתון

לאחר זיהוי של נגדים מחוברים בטור:

כאשר:

לאחר זיהוי של נגדים מחוברים במקביל:

כאשר:

נציב נתונים ונקבל:

אותו הזרם עבור דרך ו-. מאחר והם מחוברים בטור, סך ההתנגדות היא:

לכן הזרם (לפי חוק אוהם):

נציב נתונים:

שאלה 9

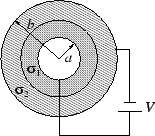
הנגד הנתון בשאלה

סעיף א’

נחשב את ההתנגדות של קליפה כדורית עבה כללית, באותו אופן כמו התנגדות של גליל עבה. נניח כי (בלי קשר לשאלה) שלקליפה הכדורית רדיוס חיצונית ורדיוס פנימי .

מבחינה דיפרנציאלית, כל קליפה דקה תורמת:

נסכום אינטגרלית:

נוכל להפריד את הנגד לשניים לפי המוליכות הסגולית שלו. נציב עבור כל חלק את הנוסחה שמצאנו (כעת ו- שונים):

שני הנגדים מחוברים בטור, ולכן:

נציב נתונים ונקבל:

סעיף ב’

הזרם דרך כל הקליפה צריך להיות זהה, ולכן:

נרצה למצוא את צפיפות המטען ב- :

ולכן:

מחוק אוהם המיקרוסקופי, ב-:

נציב נתונים ונקבל:

שאלה 10

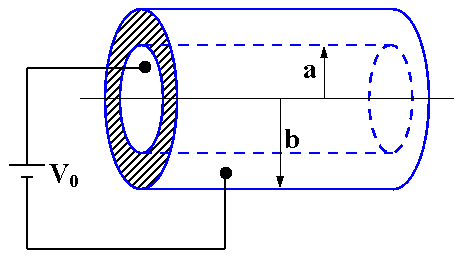
הגליל הנתון בשאלה

נחשב באותו אופן כמו התנגדות של גליל עבה. מבחינה דיפרנציאלית, כל קליפה דקה תורמת:

נסכום אינטגרלית:

נשים לב ש- תלוי ב-:

ולכן: