תורת היחסות הפרטית
נביט במערכת שכוללת רכבת הנעה במהירות קבועה ביחס לרציף. על הרציף עומד אדם אחד וברכבת ישב אדם אחר.
ברגע שהם חולפים זה ליד לזה, השעונים שלהם מסונכרנים. היגיון הבריא אומר שבכל רגע בהמשך, השעונים שלהם יראו את אותו זמן. כלומר, שקיים זמן אבסולוטי ליקום. תוצאה זו נכונה בתוך טווח השגיאה של ניסויים במהירויות קטנות משמעותית מ-
תורת היחסות הפרטית דנה בתרגום של מיקום וזמן מאורעות בין מערכות ייחוס הנעות במהירות קבועה אחת ביחס לשנייה. (מערכות אינרציאליות). מכיוון שתורה זו דנה רק במערכות ייחוס שאינן מאיצות, מוסיפים לה את התיאור תורת היחסות הפרטית. ב-1917 איינשטיין פרסם את תורת היחסות הכללית הכוללת אפקטים של תאוצה.
עקרונות תורת היחסות
תורת היחסות הפרטית בנויה על שני עקרונות:
חוקי הפיזיקה זהים בכל מערכת ייחוס אינרציאלית. כלומר, אין מערכת ייחוס אינרציאלית אחת עדיפה על מערכת אחרת. גם גליליאו הניח שחוקי המכניקה הם זהים בכל מערכת ייחוס אינרציאלית. איינשטיין הכללי רעיון זה לכלול אלקטרומגנטיות ואופטיקה. שימו לב שהחוק אינו אומר שהמדידות של גדים פיזיקליים שווים בכל מערכת ייחוס. מדידית המהירות, לדוגמה, משתנה במערכות ייחוס שונות. ההנחה היא שהחוק שמקשר בין הגדלים הנמדדים זהים.
מהירות האור היא קבועה בכל הכיוונים ובכל מערכות הייחוס. דרך אחרת להציג עקרון זה הוא שקיים בטבע מהירות מקסימלית אותה לא ניתן לעבור. נסמן את המהירות הזאת באות
שני העקרונות נבדקו ניסיונית במשך עשרת שנים ולא נמצא שום סטייה.
מהירות האור
דוגמה לניסוד שבדק שלא ניתן להאיץ גוף מעבר למהירות האור נעשה ב-1964 על ידי ברטוצי . בניסוי זה הוא האיץ אלקטרונים ומדד את האנרגיה הקינטית שלהם. הוא מצא שככל שמאיצים אלקטורן האנרגיה הקינטית שלו גדלה, אבל המהירות שלו לא עוברת את מהירות האור. אלקטרונים הואצו עד כדי
מהירות האור נמדדה להיות:
התארכות זמן
בתורת היחסות הפרטית אנו נרצה לתאר איך מאורעות במערכת ייחוס אינרציאלית אחת מתורגמות למערכת ייחוס אינרציאלית אחרת.
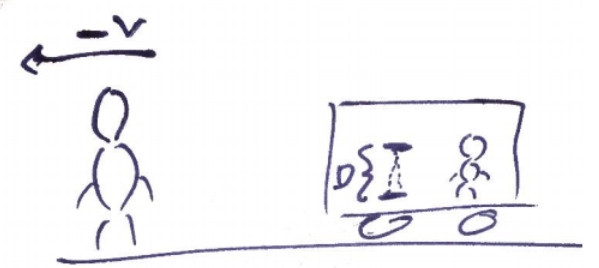
נתחיל בדוגמה שתוביל למושג של התארכות זמן . נדמיין שני אנשים, אחד על רכבת שנעה במהירות
בשעון אור, יש שתי מראות המופרדות במרחק
פרק זמן זה נקרא הזמן העצמי והוא מתאר שתי מאורעות שהתרחשו באותו מקום מבחינת האדם ברכבת : היציאה של קרן האור מהמראה התחתונה והחזרה שלה אליה.
נסמן את המאורעות בטבלה:
מאורע מערכת ייחוס הקבועה ברציף מערכת ייחוס הנעה עם הרכבת קרן האור יוצאת מהמראה התחתונה של שעון האור הנמצא על הרכבת. $$ \begin{gather}x’{1}=x \t’ {1}=t\end{gather}
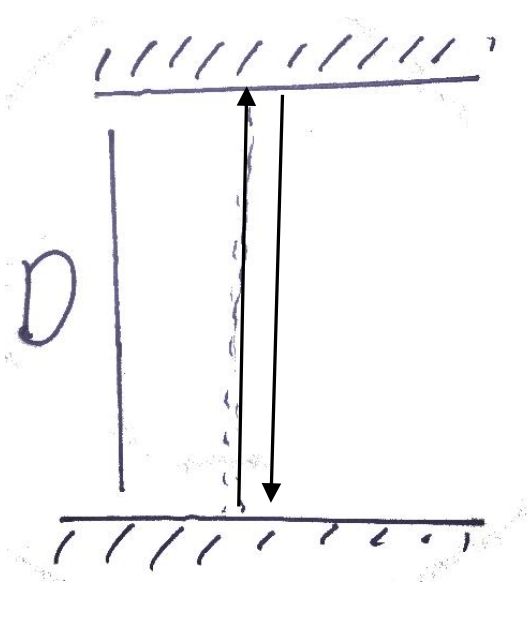
ק ר ן ה א ו ר ח ו ז ר ת ל מ ר א ה ה ת ח ת ו נ ה ש ל ש ע ו ן ה א ו ר ה נ מ צ א ע ל ה ר כ ב ת ל מ ע ש ה ח ל ק ג ד ו ל מ ה פ ת ר ו ן ש ל כ ל ת ר ג י ל ב י ח ס ו ת פ ר ט י ת ה ו א ל ז ה ו ת ב צ ו ר ה נ כ ו נ ה א ת ה מ א ו ר ע ו ת ת ו ר ת ה י ח ס ו ת ה פ ר ט י ת ת א פ ש ר ל נ ו ל ת ר ג ם א ת ה מ א ו ר ע ו ת ב י ן מ ע ר כ ו ת י י ח ו ס א י נ ר צ י א ל י ו ת ש ו נ ו ת נ ח ז ו ר ל ד ו ג מ ה א נ ו נ ר צ ה ל ד ע ת מ ה פ ר ק ה ז מ ן ב י ן א ו ת ן ש ת י מ א ו ר ע ו ת כ פ י ש נ צ פ ה מ מ ע ר כ ת י י ח ו ס ה ק ב ו ע ה ב ר צ י ף ב מ י ל י ם א ח ר ו ת ג ם א ד ם ה ע ו מ ד ע ל ה ר צ י ף מ ו ד ד א ת פ ר ק ה ז מ ן ש ע ב ר ב י ן א ו ת ן ש ת י ה מ א ו ר ע ו ת ש מ ד ד ה א ד ם ב ר כ ב ת ה י צ י א ה ש ל ק ר ן ה א ו ר מ ה מ ר א ה ה ת ח ת ו נ ה ש ע ל ה ר כ ב ת ו ה ח ז ר ה ש ל ה א ל י ה נ ש י ם ל ב ש מ ב ח י נ ת ה א ד ם ע ל ה ר צ י ף ש ת י ה מ א ו ר ע ו ת ל א י ת ר ח ש ו ב א ו ת ו מ ק ו ם ל מ ע ש ה מ ב ח י נ ת ו ה א ו ר ע ב ר מ ר ח ק ש ל ו ל כ ן ה ז מ ן ש ז ה ל ק ח ה ו א \Delta t=\frac{2L}{c}
נ ש י ם ל ב מ ה ע י ק ר ו ן ה ש נ י ש ל ת ו ר ת ה י ח ס ו ת ש מ ה י ר ו ת ה א ו ר ז ה ה ב ש ת י מ ע ר כ ו ת ה י י ח ו ס מ ע ר כ ת א ח ת ק ב ו ע ה ע ל ה ר צ י ף ו ה ש נ י י ה ק ב ו ע ה ב ר כ ב ת מ כ י ו ו ן ש מ ה י ר ו ת ה א ו ר ק ב ו ע ה ו ה א ו ר ע ו ב ר ד ר ך א ר ו כ ה י ו ת ר מ ב ח י נ ת ה א ד ם ה ע ו מ ד ע ל ה ר צ י ף א נ ו ר ו א י ם ש פ ר ק ז מ ן ז ה ג ד ו ל מ פ ר ק ה ז מ ן ש מ ד ד ה א ד ם ה י ו ש ב ב ר כ ב ת כ ל ו מ ר מ ב ח י נ ת ה א ד ם ע ל ה ר כ ב ת ע ב ר פ ח ו ת ז מ ן מ א ש ר ה א ד ם ע ל ה ר צ י ף נ ח ש ב א ת ה י ח ס ב י ן ה ז מ ן ב א ו פ ן מ ד ו י ק מ מ ש פ ט פ י ת ג ו ר ס L=\sqrt{ \left( \frac{1}{2}v\Delta t \right)^{2}+D^{2} }
נ צ י ב ב מ ש ו ו א ה ז ו א ת ש ח י ל צ נ ו מ ה מ ש ו ו א ה ה ק ו ד מ ת ו נ ק ב ך \begin{gather}
כ ל ו מ ר מ צ א נ ו כ י \Delta t=\dfrac{\Delta {t}_{0}}{\sqrt{ 1-\frac{v^{2}}{c^{2}} }}
מ כ י ו ו ן ש מ ה י ר ו ת ה ר כ ב ת ת מ י ד ק ט נ ה מ מ ה י ר ו ת ה א ו ר ה מ כ נ ה ת מ י ד ח י ו ב י ו ק ט ן מ א ח ד מ כ א ן ש נ י ת ן ל ז כ ו ר ת ו צ א ה ז א ת ע ל י ד י ה מ ש פ ט \text{Moving clocks run slow}
א נ ו ר ו א י ם ת ו צ א ה ז ו מ ה א י ו ר ל מ ע ל ה מ ב ח י נ ת ה א ד ם ה ע ו מ ד ע ל ה ר צ י ף ה ש ע ו ן ע ל ה ר כ ב ת מ ת ק ת ק י ו ת ר ל א ט ת ו פ ע ה ז ו נ ק ר א ת ה ת א ר כ ו ת ז מ ן מ ש מ ע ו ת ה ש פ ר ק ה ז מ ן ב י ן ש ת י מ א ו ר ע ו ת ש י ת ר ח ש ו ב א ו ת ו מ ק ו ם מ ב ח י נ ת מ ע ר כ ת י י ח ו ס א ח ת י ת ר ח ש ו ב פ ר ק ז מ ן י ו ת ר א ר ו ך מ ב ח י נ ת מ ע ר כ ת י י ח ו ס ה נ ע ה ב מ ה י ר ו ת ק ב ו ע ה ב י ח ס ל מ ע ר כ ת ה ר א ש ו נ ה ב ת ו ר ת ה י ח ס ו ת נ ה ו ג ל ה ג ד י ר א ת ה ג ד ל י ם ה ג ד ר ה ה ג ד ר ה מ כ א ן ש ה ז מ ן ש י ב ר ב י ן ש ת י ה מ א ו ר ע ו ת י צ י א ת ק ר ן ה א ו ר מ ה מ ר א ה ה ת ח ת ו נ ה ש ע ל ה ר כ ב ת ו ה ח ז ר ה ש ל ה א ל י ה כ פ י ש מ ד ד ו ה צ ו פ ה ע ל ה ר כ ב ת ו ה צ ו פ ה ע ל ה ר צ י ף מ ק י י מ ו ת א ת ה ק ש ר \Delta=\gamma\Delta {t}_{0}
You can't use 'macro parameter character #' in math mode תוצאה זו מתרגמת את מדידת הזמן העצמי שמודד צופה במערכת בה המאורעות התרחשו באותו מקום במרחב למדידת הזמן של צופה במערכת ייחוס אינרציאלית אחרת. התוצאה נכונה לא רק עבור מחזור אחד של שעון האור, אלא לכל פרק זמן שעבר. נשים לב שהתוצאה נכונה רק עבור מדידת זמן עצמי. >[!example] דוגמה: > >אתם יושבים במנוחה בחללית שעוברת ליד כדור הארץ עם מהירות יחסית של $0.999\,c$. לידכם שעון אור. מהרג שעברתם את כדור הארץ מדדתם שעברו $10$ שנים. בזמן זה אתם מסתובבים וחוזרים לכדור הארץ באותה מהירות. הדרך חזרה לוקחת לכם (מבחינתכם) עוד $10$ שנים. >כמה זמן האנשים על כדור הארץ מדדו שלקח המסע שלכם? אנו נזניח כל אפקט של עצירת ותאוצת החללית. >![[PHY1_010 תורת היחסות הפרטית 2023-06-23 22.21.20.excalidraw.svg]] > **פתרון**: > בבעיה זו יש שתי מערכות ייחוס אינרציאליות, אחת על כדור הארץ והשנייה על החללית. מדידת הזמן שלכם בדרך הלוך היא הזמן העצמי מכיוון שהמאורעות שמדדתם (פגיעת האור הלוך חזור במראה התחתונה של שעון האור שלידכם) התרחשו באותו מקום ביחס אליכם. כלומר בדרך הלוך: > $$ > \Delta {t}_{0}=10 \, \text{years} > $$ > מבחינת דור הארץ הזמן שעבר חייב להיות גדול מ-$10$ שנים. נחשב אותו: > $$ > \Delta {t}_{0}=\gamma\Delta {t}_{0}=\dfrac{\Delta {t}_{0}}{\sqrt{ 1-\dfrac{v^{2}}{c^{2}} }}=\dfrac{\pu{10 years}}{\sqrt{ 1-\left(\dfrac{0.999\,c}{c}\right)^{2} }}=\pu{224 years} > $$ > החישוב עבור הזמן שעבר בדרך חזרה זהה ולכן נמצא שסך הכל במהלך המסע שלכם שלקח $20$ שנה (מבחינתכם), על כדור הארץ עברו: > $$ > \Delta t_{\text{total}}=\pu{448 years} > $$ ### פרדוקס התאומים נביט בדוגמה הקודמת. אמרנו שמהירות היא יחסית. איך אפשר לדעת שנוסע אחד נע והשני נח? כל שצריך הוא להפוך את נקודת המבט ונגיע למסקנה ההפוכה. כלומר, ניקח את החללית כמערכת המנוחה. במקרה זה כדור הארץ נע במהירות $0.999\,c$ בכיוון ההפוך למשך $10$ שנים וחוזר למשך $10$ שנים. לפי אותו פתרון שעשינו הרגע, נגלה שהצופה על הארץ הזדקן ב-$20$ שנה, בעוד שהאדם בחללית הזדקן ב-$448$ שנה. נראה שיש כאן פרדוקס, שנקרא **פרדוקס התאומים**. מחיפוש קצר בגוגל, קל למצוא פתרון זריז לפרדוקס:  אבל מחיפוש יותר עמוק, הבעיה היא למעשה יותר גדולה:  # טרנספורציית לורנץ מאורע שהתרחש במערכת ייחוס $S$ יהיה בעל קואורדינטות $(x,y,z,t)$. אותו מאורע שיתרחש במערכת ייחוס $S'$ יהיה בעל קואורדינטות $(x',y',z',t')$. ה[[ALG1_009 טרנספורמציות לינאריות#טרנספורמציה-לינארית|טרנספורמציה]] שמשקשרת בין קואורדינטות המאורע במערכות הייחוס השונות היא **טרנספורמציית לורנץ**. כדי להקל על עצמינו, נניח תמיד ששתי מערכות הצירים מקבילות. נניח עוד שמערכת הייחוס $S'$ נעה במהירות קבועה $v$ ביחס למערכת הייחוס $S$. עוד נניח שראשית שתי המערכות מתלכדות ברגע $t=t'=0$. ![[PHY1_010 תורת היחסות הפרטית 2023-06-24 10.41.41.excalidraw.svg]] אם אות של אור נשלח מהראשית של שתי מערכות הייחוס בזמן $0$, אות זה מתפשט במרחב במהירות אחידה בכל הכיוונים. כלומר, נקבל שהמרחק של האות מהראשית בזמן $t$ במערכת $S$ מקיימת: \begin{gather}
נ ש י ם ל ב ש ה ג ו ד ל ה ו א ר ד י ו ס ש ל כ ד ו ר א ל י ו ה א ו ר ה ג י ע כ ד ו ר ז ה נ ק ר א כ ד ו ר ה א ו ר נ ג ד י ר א ת ל ה י ו ת ל ד ג ו מ ה כ ד ו ר ה א ר ץ מ ש ד ר ג ל י ר ד י ו ל ח ל ל ג ל י ה ר ד י ו ה א ל ה נ ע י ם ב מ ה י ר ו ת ה א ו ר מ כ א ן ש ר ק כ ו כ ב י ל כ ת ב מ ר ח ק ש ל ע ד כ א ש ר ה ו א ה ז מ ן מ ש י ד ו ר ה ר ד י ו ה ר א ש ו ן י ח ש פ ו ל ג ל י ה ר ד י ו ה א ל ה ת ו ר ת ה י ח ס ו ת ה פ ר ט י ת כ ל ו מ ר מ צ א נ ו כ א ן ג ו ד ל א י נ ו ו ר י א נ ט י ג ו ד ל ש א י נ ו מ ש ת נ ה ב י ן מ ע ר כ ו ת י י ח ו ס ב מ י ל י ם א ח ר ו ת ב כ ל מ ע ר כ ת י י ח ו ס א י נ ר צ י א ל י ת ה ג ו ד ל ש מ ו ג ד ר ע ל י ד י ס כ ו ם ר י ב ו ע י ה ק ו א ו ר ד י נ ט ו ת ה מ ר ח ב י ו ת פ ח ו ת ה מ כ פ ל ה ש ל ר י ב ו ע מ ה י ר ו ת ה א ו ר ב ר י ב ו ע ה ז מ ן ש ח ל ף ב א ו ת ה מ ע ר כ ת י י ח ו ס ש ו ו ה ל ע ל י ד י ה ע ב ר ת א ג פ י ם נ ק ב ל (\Delta S)^{2}=c^{2}t^{2}-x^{2}-y^{2}-z^{2}=0=c^{2}t’^{2}-x’^{2}-y’^{2}-z’^{2}=0
You can't use 'macro parameter character #' in math mode אנו נדרוש שהטרנספורמציה שמקשרת בין מערכות ייחוס ישמרו על הגודל $(\Delta S)^{2}$ אינוואריאנטי. >[!def] הגדרה: > >**טרנספורמציית לורנץ** היא: >$$ > \begin{aligned} > &t'=\gamma\left( t-\frac{\beta}{c}x \right) \\ > &x'=\gamma(x-vt) \\ > &y'=y \\ > &z'=z \\ > \end{aligned} > $$ >הטרנספורמצייה ההפוכה: >$$ > \begin{aligned} > &t=\gamma\left( t'+ \frac{\beta}{c}x' \right) \\ > &x=\gamma(x'+vt') \\ > &y=y' \\ > &z=z' \\ > \end{aligned} > $$ >[!notes] הערות: > >1. עבור מהירויות קטנות מאוד ממהירויות האור, $\frac{v}{c}\ll 1$, נקבל $\beta \to 0$ ו-$\gamma \to 1$ ומכאן שטרנספורמציית לורנץ הופכת ל[[PHY1_004 תנועה הרמונית ומערכות ייחוס#טרנספורמציית-גלילאו|טרנספורמציית גלילאו]]: > $$ > \begin{aligned} > &t'=t \\ > &x'=x-vt \\ > &y'=y \\ > &z'=z > \end{aligned} > $$ ביחסות פרטית אנו מתארים איך מיקום וזמן של מאורעות במערכת ייחוס אחת מתורגמות למערכת ייחוס אחרת. כלי עזר שיעזור לנו לא להתבלבל בין מערכות הייחוס הוא טבלת מאורעות: | מאורע | מערכת ייחוס $S$ | מערכת ייחוס $S'$ | | ----- | ------------------------------------------------- | ----------------------------------------------- | | | $$ \begin{gather}{x}_{1}= \\{t}_{1}=\end{gather} $$ | $$ \begin{gather}x'_{1}= \\t'_{1}=\end{gather} $$ | | | $$ \begin{gather}{x}_{2}= \\{t}_{2}=\end{gather} $$ | $$ \begin{gather}x'_{2}=\\t'_{2}=\end{gather} $$ | כאשר התרגום בין מערכות הייחוס תעשה באמצעות טרנספורמציית לורנץ. נראה אם טרנספורמציית לורנץ משחזרת את התארכות הזמן. אם נמדוד את הפרש הזמנים בין שתי מאורעות במערכת $S$ שמתרחשות באותה נקודה במרחב, ${x}_{1}={x}_{2}$, נקבל שבמערכת $S'$ הפרש הזמנים הינו: t’{2}-t’ {1}=\Delta t’=\gamma\left( {t}{2}-\frac{\beta}{c}{x} {2} \right)-\gamma\left( {t}{1}-\dfrac{\beta}{c}{x} {1} \right)=\gamma({t}{2}-{t} {1})=\gamma\Delta {t}_{0}
You can't use 'macro parameter character #' in math mode כאשר סימנו את פרק הזמן בין שתי המאורעות במערכת $S$ כהזמן העצמי $\Delta {t}_{0}$ משום שהם יתרחשו באותה נקודה במרחב במערכת זו. אנו רואים שקיבלנו את אותה תוצאה שקיבלנו מקודם ([[#התארכות-זמן|התארכות זמן]]). אנו רואים מדוגמה זו שהזמן העצמי בין שני מאורעות הוא הזמן הקצר ביותר. ## התקצרות אורך נניח מוט שנמצא במנוחה במערכת $S$. אורך המוט במערכת זו הוא ${L}_{0}$. מאחר והוא במנוחה, מיקום קצוות המוט לא תלויות בזמן. נקרא ל-${L}_{0}$ **אורך המנוחה**. מה יהיה אורך המוט במערכת $S'$? ![[PHY1_010 תורת היחסות הפרטית 2023-06-24 12.19.37.excalidraw.svg]] כדי למדוד את אורך המוט, על צופה ב-$S'$ למדוד את מיקום קצוות המוט באותו זמן $t'$. הדרישה למדוד באותו זמן היא חשובה מכיוון שמוט זז מבחינת מערכת $S'$. לכן אם נמדוד כל קצה של המוט בזמן שונה, נקבל מדידה שלא משקפת את אורך המוט. רק מדידה באותו זמן תהיה הגדרה הגיונית לאורך המוט. מכאן שטבלת המאורעות היא: | מאורע | מערכת ייחוס $S$ | מערכת ייחוס $S'$ | | -------------------------------------- | -------------------------------------------------------------- | --------------------------------------------------- | | מדידת קצה אחד של אורך המוט במערכת $S'$ | $$ \begin{gather}{x}_{1}=\gamma({x}_{1}'+vt'_{1})\end{gather} $$ | $$ \begin{gather}x'_{1} \\t'_{1}\end{gather} $$ | | מדידת קצה שני של אורך המוט במערכת $S'$ | $$ \begin{gather}{x}_{2}=\gamma(x'_{2}+vt'_{2})\end{gather} $$ | $$ \begin{gather}x'_{2}\\t'_{2}=t'_{1}\end{gather} $$ | לכן: {L}{0}={x} {2}-{x}{1}=\gamma(x’ {2}+vt’{2})-\gamma(x’ {1}+vt’{1})=\gamma(x’ {2}-x’_{1})=\gamma L’
כ א ש ר ה ג ד ר נ ו א ת ל ה י ו ת ה א ו ר ך ש ל ה מ ו ט כ פ י ש נ מ ד ד ב מ ע ר כ ת מ כ א ן א נ ו מ ו צ א י ם ש \begin{gather}{0}=\gamma L’ \ {0}}{\gamma}<{L}_{0}
You can't use 'macro parameter character #' in math mode כלומר, מבחינת הצופה במערכת $S'$, אורך המוט הוא קצר יותר! >[!example] דוגמה: > >נתבונן בחללית הנעה במהירות $V$ בין כדור הארץ לירח: > > ![[PHY1_010 תורת היחסות הפרטית 2023-06-24 12.36.22.excalidraw.svg]] >מבחינת צופה בחללית, המסה לוקח זמן $\Delta {t}_{0}$. זהו הזמן העצמי מאחר ומבחינת החללית, כדור הארץ והירח נמצאים באותו מקום, פשוט בזמן שונים. >לעומת זאת, מבחינת צופה על כדור הארץ, הזמן שלקח לחללית להגיע לירח הוא ארוך יותר בפקטור $\gamma$. נשים לב שביחס לצופה במנוחה בחללית, כדור הארץ והירח נעים במהירות $-V$. > מיקום הירח ביחס לצופה בכדור הארץ הוא קבוע, לכן המרחק שהוא מודד הוא אורך המנוחה, ${L}_{0}$. > >נשים לב שהצופה מהחללית והצופה על כדור הארץ יסכימו על גודל המהירות היחסית בינהם. בפרט, שניהם יסכימו שהם עצמם במנוחה והשהצופה השני מתרחק מהם במהירות בגודל $V$. מכיוון שמהירות זו היא $V=\dfrac{\text{length}}{\text{time}}$, ומכיוון שהצופים השונים מודדים זמנים שונים, עליהם גם למדוד אורכים שונים. בפתירת תרגילים עוזר מאוד להצליח להגדיר איזה צופה מודד את הזמן העצמי ואיזה צופה מודד את אורך המנוחה. מכאן אנו יודעים לקשר בין הזמנים והאורכים בין מערכות הייחוס בעזרת: >[!formula] נוסחה: > >$$ > \begin{gather} > L'=\frac{{L}_{0}}{\gamma} \\ > \Delta t=\gamma\Delta {t}_{0} > \end{gather} > $$ ## סימולטניות נדמיין רכבת שנעה במהירות $V$ ביחס לרציף. ברגע שמרכז הרכבת עוברת ליד צופה על הרציף, הצופה רואה שני ברקים פוגעים בקצוות הרכבת, אחת מקדימה ואחת מאחורה, באותו זמן. ![[PHY1_010 תורת היחסות הפרטית 2023-06-24 13.14.12.excalidraw.svg]] מה לגבי הצופה שיושב בתוך הרכבת? מבחינתו הוא במנוחה והעולם מסביב זז. גם הוא רואה הבזק של שני ברקים שפגעו ברכבת, אבל מבחינתו האור מהברק שפגע בקדמת הקרון הגיע אליו ראשון. ![[PHY1_010 תורת היחסות הפרטית 2023-06-24 12.51.37.excalidraw.svg]] בסוף הנסיעה הוא הולך לבדוק את קצוות הקרון ורואה שאכן פגע הם ברק. מכיוון שהוא ישב במרכז הרכבת והברקים, ומאחר והאור מהברק שפגע בקדמת הרכבת הגיע אליו לפני האור מהברק שפגע בקצה האחורי, הוא מגיע למסקנה שברק פגע קודם בקצה הימני ורק לאחר מכן בקצה השמאלי. מכאן אנו רואים שאירועים שנראים **סימולטניים** במערכת ייחוס אחת, אינם סימולטניים במערכת ייחוס אחרת. נראה זאת בעזרת טרנספורמציית לורנץ. הפרש הזמנים בין מאורעות במערכת $S$ למערכת $S'$ הוא: \Delta t’=\gamma\left( \Delta t- \dfrac{v\Delta x}{c^{2}} \right)
ע ב ו ר ה ד ו ג מ ה ע ם ה ר כ ב ת ב מ ר כ ת ה צ ו פ ה ר א ה ש ש נ י ה ב ר ק י ם פ ג ע ו ב א ו ת ו ה ז מ ן ו מ ב ר ח ק מ כ א ן ש ב מ ע ר כ ת ה ר כ ב ת ה ב ר ק י ם פ ג ע ו ב ה פ ר ש ז מ נ י ם \Delta t’=\gamma\left( -\dfrac{v\Delta x}{c^{2}} \right)
You can't use 'macro parameter character #' in math mode נשים לב שמבחינת הצופה ברכבת, ${t}_{1}<{t}_{2}$. אנו רואים שאפילו אם מאורעות התרחשו באותו זמן מבחינת צופה במערכת אחת, העבודה שהם התרחשו במקומות זונים במרחב משנות את הפרש הזמנים בהם צופה במערכת אחרת יצפה בהם. זאת דוגמה לערבוב בין זמן ומרחב ביחסות פרטית. בפרט, אנו רואים שמאורעות שהתרחשו סימולטנית עבור צופה במערכת ייחוס אינרציאלית אחת לא התרחשו סימולטנית עבור צופה במערכת ייחסו אינרציאלית אחרת.  ## טרנספורמציית לורנץ למהירות נניח שמדדנו את המקום של גוף כלשהו בשני זמנים שונים במערכת ייחוס $S$. עבור המדידות אנו יודעים את $\Delta t,\Delta x,\Delta y$. מכאן שהמהירות הממוצעת של הגוף היא: \begin{gather}{x}=\frac{\Delta x}{\Delta t} \[2ex] {y}=\frac{\Delta y}{\Delta t}
א ם נ י ק ח א ת ה ג ב ו ל ב ו נ ק ב ל א ת ה מ ה י ר ו ת ה ר ג ע י ת ר א י נ ו ע ד כ ה ש צ ו פ י ם ב מ ע ר כ ו ת י י ח ו ס ש ו נ ו ת מ ו ד ד י ם ז מ נ י ם ו א ו ר כ י ם ש ו נ י ם ע ב ו ר א ו ת ן מ א ו ר ע ו ת נ ת ע נ י י ן כ ע ת מ ה ה מ ה י ר ו ת ש ל ה ג ו ף כ פ י ש נ מ ד ד ה ב מ ע ר כ ת ה י י ח ו ס ש נ ע ה ב מ ה י ר ו ת ב י ח ס ל מ ע ר כ ת ה י י ח ו ס מ ט ר נ ס פ ו ר מ צ י י ת ל ו ר נ ץ א נ ו י ו ד ע י ם ש \begin{gather}
ש י מ ו ל ב ה ז ה ל א ה נ ג ז ר ת ז ה פ ש ו ט ב מ ע ר כ ת י י ח ו ס נ ח ש ב א ת ה מ ה י ר ו ת ה מ מ ו צ ע ת ב מ ע ר כ ת ה י י ח ו ס u_{x’}= \dfrac{\Delta x’}{\Delta t’}=\dfrac{\gamma(\Delta x-v\Delta t)}{\gamma\left( \Delta t-\dfrac{v}{c^{2}}\Delta x \right)}=\dfrac{\dfrac{\Delta x}{\Delta t}-v}{1-\dfrac{v}{c^{2}}\dfrac{\Delta x}{\Delta t}}=\dfrac{u_{x}-v}{1-\dfrac{v}{c^{2}}u_{x}}\xrightarrow[\Delta t \to 0]{} \dfrac{u_{x}-v}{1-\dfrac{v}{c^{2}}u_{x}}
כ א ש ר ב ש ו ו י ו ן ה ש ל י ש י ה ו צ א נ ו מ ח ו ץ ל ס ו ג ר י י ם ע ב ו ר ה מ ה י ר ו ת ב כ י ו ו ן נ ק ב ל \begin{aligned}
כ ל ו מ ר מ צ א נ ו מ ש פ ט ט ר נ ס פ ו ר מ צ י י ת ל ו ר נ ץ ל מ ה י ר ו ת ה י א ה ט ר נ ס פ ו ר מ צ י ה ה ה פ ו כ ה נ ש י ם ל ב ש ב ג ב ו ל ה ק ל א ס י נ ק ב ל \begin{gather}
You can't use 'macro parameter character #' in math mode כפי שקיבלנו בטרנספורמציית גלילאו. מכיוון שהשתמשנו בטרנספורמציית לורנץ, טרנספורמציית לורנץ למהירות שומרת שהגוף לא יעבור את מהירות האור. נראה זאת בדוגמה הבאה: >[!example] דוגמה: > >קרן אור נעה במהירות $u_{x}=c\,\hat{\mathbf{x}}$ במערכת ייחוס אינרציאלית $S$. מה מהירות הקרן במערכת ייחוס אינרציאלית אחרת, $S'$, הנעה במהירות $v\,\hat{\mathbf{x}}$ ביחס למערכת הנתונה? >![[Pasted image 20230625094528.png|book]] >**פתרון**: >נשתמש בטרנספורמציית לורנץ למהירות כדי לתרגם בין מהירות קרן האור במערכות הייחוס השונות. במערכת ייחוס הנעה במהירות $v\,\hat{\mathbf{x}}$ ביחס למערכת הנתונה נקבל שמהירות הקרן היא: >$$ > u_{x'}= \dfrac{u_{x}-v}{1-\dfrac{v}{c^{2}}u_{x}}=\dfrac{c-v}{1-\dfrac{v}{c}}=\dfrac{c-v}{\dfrac{c}{c}-\dfrac{v}{c}}=c > $$ >כלומר, טרנספורמציית לורנץ למהירות מקיימות את התנאי שמהירות האור היא אותו דבר בכל מערכת ייחוס אינרציאלית. לשם ההמחשה נניח שקרן האור נעה על רציף תחנת רכבת (מערכת $S$). מה מהירות הקרן כפי שרואה צופה ברכבת הנעה במהירות $v=0.8c$ (מערכת $S'$)? כפי שראינו בפתרון הדוגמv, גם לצופה בתוך הרכבת מהירות קרן האור היא $c$! >[!example] דוגמה: > >שתי חלליות, $A$ ו-$B$, יוצאות בו זמנית בזמן $t=0$ מאותה נקודה בכדור הארץ. ביחס לכדור הארץ, חללית $A$ נעה במהירות $v_{A}=\frac{1}{2}c\,\hat{\mathbf{x}}$ וחללית $B$ נעה במהירות $v_{B}=-\frac{1}{2}c\, \hat{\mathbf{y}}$. >מה גודל המהירות של חללית $B$ ביחס לצופה בחללית $A$? > >![[Pasted image 20230625094723.png|book|400]] >**פתרון**: >נשים לב שהשאלה מבקשת לתרגם בין מהירויות הנמדדות בכדור הארץ למהירויות הנמדדות בחללית $A$. לשם כך, נשתמש בטרנספורמציית לורנץ למהירות על מנת למצוא את המהירות ביחס לחללית $A$. >נקרא למערכת כדור הארץ מערכת $S$, ולמערכת הקבועה על חללית $A$ כמערכת $S'$. מכאן ש: >$$ > \begin{aligned} > &u_{B,x'}=\dfrac{u_{x}-V}{1-\dfrac{v}{c^{2}}u_{x}}=\dfrac{0-\dfrac{1}{2}c}{1-0}=-\frac{1}{2}c \\ > &u_{B,y'}=\dfrac{\sqrt{ 1-\left( \dfrac{v}{c} \right)^{2} }u_{y}}{1-\dfrac{v}{c^{2}}u_{x}}=\dfrac{\sqrt{ 1-\left( \dfrac{1}{2} \right)^{2} }\left( - \dfrac{1}{2}c \right)}{1-\dfrac{\left( \dfrac{1}{2} \right)}{c}\cdot 0}=\sqrt{ \frac{3}{4} }\left( -\dfrac{1}{2}c \right)=-\dfrac{\sqrt{ 3 }}{4}c > \end{aligned} > $$ >מכאן שגודל המהירות של חללית $B$ ביחס לחללית $A$ היא: >$$ > u_{B'}=\sqrt{ \left( -\frac{1}{2}c \right)^{2}+\left( -\dfrac{\sqrt{ 3 }}{4}c \right)^{2} }=\dfrac{\sqrt{ 7 }}{4}c > $$ >[!Question]- אבל לא לוקח זמן לאור להגיע מחללית $B$ לחללילת $A$ ולהפך? > >כן. בשאלה, אנו מניחים כבר ש-$B$ התחיל לראות את $A$ ולהפך. אנו לא עוסקים בשאלה *כמה* זמן לקח ל-$B$ להבחין בתנועה של $A$. זוהי שאלה לנושא אחר. ## סיבתיות נצייר גרף שבו הציר האופקי מייצג מקום והציר האנכי מייצג זמן עבור מערכת ייחוס מסוימת. אם קרן אור יוצאת מהראשית בזמן $t=0$, אז מיקום הקרן בכל זמן אחר ינתן על ידי $x=ct$. הקו המתאר את תנועת קרן האור בגרף שתיארנו נראה כמו קונוס, ולכן גרף זה נקרא קונוס האור. נשים לב שכל גוף בעל מסה שיוצא מהראשית ב-$t=0$ ימצא תמיד בתוך הקונוס (כי הוא ינוע במהירות נמוכה ממהירות האור). ![[Pasted image 20230625094847.png|book|400]] ביחס ל-$t=0$ שבחרנו, כל מאורע שנמצא ב-$t<0$ נמצא בקונוס התחתון (שנקרא קונוס העבר) וכל מאורע שהתרחש ב-$t>0$ נמצא בקונוס העתיד. אנו רואים שמאורע ב-$t=0$ לא יכול להשפיע על מאורעות מחוץ לקונוס האור, משום שאפילו אור לא היה מספיק להגיע למאורע מחוץ לקונוס זה. בפרט, מאורע בנקודה $A$ יכול להשפיע על מאורע בנקודה $B$, אבל לא על מאורע בנקודה $D$. זה משום שאלו מאורע $A$ היה משפיע על מאורע $D$, אז האינפורמציה בין המאורעות הייתה נעה במהירות גדולה ממהירות האור. **סיבתיות** מתייחסת לכך ששתי מאורעות יכולות להשפיע אחת על השנייה רק אם האינפורמציה העוברת ביניהן נעה במהירות קטנה ממהירות האור. # דינמיקה יחסותית עד עכשיו דנו בצורה אינטנסיבית בהשלכות של מהירות אור קבועה ושווה בכל מערכת ייחוס אינרציאלית. עקרון זה של תורת היחסות הוביל אותנו למסקנות מפתיעות כמו התארכות זמן, התקצרות אורך ולכך שסימולטניות היא דבר יחסי. למעשה, עקרון זה הוביל למסקנה שצריך למצוא טרנספורמציה שונה מטרנספורמציית גלילאו עבור מהירויות המתקרבות למהירות האור. כעת נתייחס לאקסיומה השנייה של תורת היחסות הפרטית: חוקי הפיסיקה זהים בכל מערכת ייחוס אינרציאלית. עבור מהירויות קטנות בהרבה ממהירות האור, מצאנו שהתנע של מערכת נשמר אם לא פועל עליו כוח חיצוני שקול. במקרה זה התנע של גוף מוגדר כ-$\vec{p}=m \dfrac{\mathrm{d}\vec{r}}{\mathrm{d}t}$. מה קורה עבור מהירויות המתקרבות למהירות האור? ראינו שבמהירויות אלה, צופים במערכות ייחוס שונות ימדדו זמנים שונים עבור אותן מאורעות. בעקבות תוצאות אלה, ניתן להראות שההגדרה שהשתמשנו בה עבור תנע אינה מקיימת את שימור התנע עבור צופים במערכות אינרציאליות שונות. כלומר, צופה במערכת ייחוס אחת שמודד שהתנע נשמר, לא יסכים עם צופה במערכת ייחוס אחרת, בניגוד לעקרון של תורת היחסות שדורש שחוקי הפיסיקה יהיו זהים במערכות ייחוס אינרציאליות שונות. על מנת לפתור את הבעיה שהזמנים נמדדים אחרת במערכות ייחוס שונות, אנו נמדוד את שינוי ההעתק של הגוף ביחס לשעון שנמצא על הגוף הנע. שעון זה מודד את הזמן העצמי, ${t}_{0}$, עבור שינוי ההעתק של הגוף. נגדיר את **התנע היחסותי** (כלומר התנע שנכון עבור כל מהירות, גם מהירויות הקרובות למהירות האור), כ: \vec{p}=m \dfrac{\mathrm{d}\vec{r}}{\mathrm{d}{t}{0}}=m \dfrac{\mathrm{d}\vec{r}}{\mathrm{d}t} \dfrac{\mathrm{d}t}{\mathrm{d}{t} {0}}=m \dfrac{\mathrm{d}\vec{r}}{\mathrm{d}t}\gamma=\gamma m\vec{v}= \dfrac{m\vec{v}}{\sqrt{ 1-\dfrac{v^{2}}{c^{2}} }}
כ א ש ר ה ש ת מ ש נ ו ב כ ך ש \begin{gather}{0} \ {0}}=\gamma
נ ש י ם ל ב ש פ ק ט ו ר ה ה ו פ י ע ב מ ע ב ר מ מ ע ר כ ת י י ח ו ס ש נ ע ה ע ם ה ח ל ק י ק ל מ ע ר כ ת ב ה א נ ו מ ו ד ד י ם א ת ה ת נ ע מ כ א ן ש מ ח ש ב י ם א ת ב ע ז ר ת מ ה י ר ו ת ה ח ל ק י ק נ ש י ם ל ב ש ע ב ו ר נ ק ב ל מ ה ש ג ו ר ר ש ה ת נ ע ה י ח ס ו ת י מ ת ל כ ד ע ם ה ת נ ע ה ק ל א ס י ש ר א י נ ו מ ו ק ד ם י ו ת ר ב ק ו ר ס \vec{p}=\gamma m\vec{v}\to m\vec{v}
You can't use 'macro parameter character #' in math mode כפי שניתן לראות בגרף הבא, ככל שמהירות הגוף מתקרבת למהירות האור, כך התנע שלו מתבדר. כלומר, על מנת להגדיל את המהירות של גוף הנע במהירות המתקרבת למהירות האור ב-$\Delta v$, יש צורך לשנות את התנע שלו בפער הולך וגדל. מהחוק השני של ניוטון אנו יודעים שכוח גורם לשינוי בתנע, $\vec{F}=\dfrac{\mathrm{d}\vec{p}}{\mathrm{d}t}$ . מכאן שנהיה קשה להאיץ את הגוף ככל שמהירותו מתקרבת למהירות האור. אכן, ניסויים במאיצי חלקיקים מראים שככל שמהירות החלקיק (לדוגמה אלקטרון) גדולה יותר, כך קשה להאיץ עוד. ![[Pasted image 20230625095040.png|book]] בדיוק כמו בגבול הקלאסי (הגבול בו המהירות של הגופים נמוכה באופן משמעותי ממהירות האור), אם לא פועל כוח חיצוני שקול על מערכת הגופים, התנע הכולל נשמר. ## אנרגיה נזכר ב[[PHY1_005 עבודה ואנרגיה#משפט-העבודה-אנרגיה|משפט העבודה אנרגיה]]: העבודה שעושה שקול הכוחות על גוף שווה לשינוי האנרגיה הקינטית שלו. על ידי שימוש בחוק השני של ניוטון, $F=\dfrac{\mathrm{d}p}{\mathrm{d}t}$, (נדון במקרים חד-ממדיים ולכן נשמיט את הכתיב הווקטורי) נמצא ש: \begin{aligned}
כ א ש ר ב ש ו ו י ו ן ה ר ב י ע י ב י צ ע נ ו א ת ה נ ג ז ר ת ש מ ו פ י ע ב ת ו ך ה א י נ ט ג ר ל ו ב ש ו ו י ו ן ה ח מ י ש י א י ח ד נ ו א ת ה ב י ט ו י י ם ב ת ו ך ה א י נ ט ג ר ל ע ל י ד י מ כ נ ה מ ש ו ת ף א ת ה א י נ ט ג ר ל ה ע ר כ נ ו ע ב ו ר ש נ י ז מ נ י ם ע ב ו ר ם מ ה י ר ו ת ה ג ו ף ה ה ת ח ל ת י ת ה י א ו ה ס ו פ י ת ה י א נ נ י ח כ ע ת ש ה ח ל ק י ק ה ת ח י ל מ מ נ ו ח ה מ כ א ן ש ה ע ב ו ד ה ש ו ו ה ל א נ ר ג י ה ה ק י נ ט י ת ש ל ה ח ל ק י ק E_{k}=\frac{mc^{2}}{\sqrt{ 1-\dfrac{v^{2}}{c^{2}} }}-mc^{2}=mc^{2}(\gamma-1)
You can't use 'macro parameter character #' in math mode ביטוי זה לא נראה כמו $\frac{1}{2}mv^{2}$. נשים לב שאם הגוף נע במהירות נמוכה כך ש- $\dfrac{v}{c}\ll1$ , נוכל לפתח את $\gamma$ לסדר ראשון ב[[CAL1_006 פולינום טיילור#פולינום-טיילור|טור טיילור]] כאשר הפרמטר הקטן הוא $\dfrac{v}{c}$. בפרט נקבל: \gamma=\frac{1}{\sqrt{ 1-\dfrac{v^{2}}{c^{2}} }}\cong 1+\dfrac{v^{2}}{2c^{2}}
כ א ש ר ה ש ת מ ש נ ו ב ט ו ר ט י י ל ו ר ע ד ל ס ד ר ר א ש ו ן ש ל ה פ ו נ ק צ י ה נ צ י ב ב ב י ט ו י ש מ צ א נ ו ל א נ ר ג י ה ק י נ ט י ת ו נ ק ב ל E_{k}=mc^{2}(\gamma-1)=mc^{2}\left( 1+\frac{v^{2}}{2c^{2}}-1 \right)= \frac{1}{2}mv^{2}
כ פ י ש ק י ב ל נ ו ב ג ב ו ל ה ק ל א ס י ה ע ר ו ת א ל ו ה י י נ ו מ פ ת ח י ם א ת ל ס ד ר א ז כ פ י ש ע ש י נ ו ע ד ע כ ש י ו ה א י נ פ ו ר מ צ י ה ע ל ה א נ ר ג י ה ה ק י נ ט י ת ה י י ת ה נ ע ל מ ת ל כ ן נ א ל צ נ ו ל ק ר ב א ת ל ס ד ר ה ב א א נ ו ר ו א י ם ע ו ד מ ה ב י ט ו י ש מ צ א נ ו ל א נ ר ג י ה ה ק י נ ט י ת ה י ח ס ו ת י ת כ י \begin{gather}
מ ב י ט ו י ז ה א נ ו ר ו א י ם כ י ה ג ו ד ל ש ו ו ה ל ס כ ו ם ש ל ה א נ ר ג י ה ה ק י נ ט י ת ו ג ו ד ל ק ב ו ע א נ ו מ ג ד י ר י ם א ת ה א נ ר ג י ה ה י ח ס ו ת י ת ה כ ו ל ל ת ש ל ח ל ק י ק ל ה י ו ת \boxed {
Erroneous nesting of equation structures מביטוי זה רואים שגם כאשר לגוף אין אנרגיה קינטית, עדיין יש לו אנרגיה $E=mc^{2}$. אנרגיה זו נקראת **אנרגיית המנוחה** ומסומנת לעיתים באות $E_{0}$. ביטוי זה נותן את השקילות בין מסה לאנרגיה. לעיתים נוח להגדיר את המסה היחסותית של גוף להיות $\gamma m$. במונחים של הגדרה זו, המסה, $m$, שמופיעה בהרצאה שלנו היא מסת המנוחה הנמדדת כאשר הגוף במנוחה. כאשר המערכת היא סגורה (לא פועלים עליה כוחות חיצוניים), האנרגיה הכוללת שלה נשמרת. >[!example] דוגמה: > >שני חלקיקים בעלי מסות $m$ ו $3m$ נעים לאורך ציר $x$ כך שלשניהם אנרגיות שוות כפי שנמדד במערכת המעבדה. ידוע שגודל מהירותו של חלקיק $3m$ ביחס למעבדה היא $0.8c$. > - מהי האנרגיה הכוללת של המערכת ביחס למערכת המעבדה? > **פתרון**: > אנו יודעים את מהירות החלקיק המסיבי יותר. מכאן שפקטור ה-$\gamma$ שלו הוא: > $$ > \gamma=\frac{1}{\sqrt{ 1-\dfrac{v^{2}}{c^{2}} }}=\frac{1}{\sqrt{ 1-0.8^{2} }}=\frac{5}{3} > $$ > בעזרת תוצאה זו נמצא שהאנרגיה של חלקיק זה ביחס למערכת המעבדה היא: > $$ > E_{3m}=\gamma 3mc^{2}=\frac{5}{3}3mc^{2}=5mc^{2} > $$ > מכיוון שנתון שלשני החלקיקים אנרגיה זהה, האנרגיה הכוללת במערכת היא: > $$ > E_{\text{tot}}=E_{m}+E_{3m}=5mc^{2}+5mc^{2}=10mc^{2} > $$ > - מה התנע הכולל של המערכת ביחס למערכת המעבדה? > **פתרון**: >התנע של החלקיק המסיבי יותר הוא: >$$ > p_{3m}=\gamma 3mv=\frac{5}{3} 3m \cdot 0.8c=4mc > $$ >עבור החלקיק בעל מסה $m$ נחשב את פקטור $\gamma$ מהביטוי לאנרגיה שלו (ששווה לאנרגיה של חלקיק $3m$ שמצאנו בסעיף א'): >$$ > \begin{gather} > E_{m}=E_{3m}=5mc^{2}=\gamma mc^{2} \\ > \gamma=5 > \end{gather} > $$ >מהביטוי ל-$\gamma$ נמצא את מהירות החלקיק: >$$ > \begin{gather} > \gamma=5=\frac{1}{\sqrt{ 1-\dfrac{v^{2}}{c^{2}} }} \\ > v=\sqrt{ \frac{24}{25} }c > \end{gather} > $$ >מכאן שהתנע של גוף זה הינו: >$$ > p=\gamma mv=5m\sqrt{ \frac{24}{25} }c=\sqrt{ 24 }mc > $$ >התנע הכולל של המערכת הוא: >$$ > p_{\text{tot}}=p_{m}+p_{3m}=\sqrt{ 24 }mc+4mc=(4+\sqrt{ 24 })mc > $$ נוסיף עוד קשר אחד מועיל עבור הגדול של התנע היחסותי. ניתן לבטא את גודל המהירות כפונקציה של פקטור $\gamma$: \begin{gather}
נ צ י ב ב ב י ט ו י ע ב ו ר ת נ ע ו נ ק ב ל p=\sqrt{ \gamma ^{2}-1 },, mc
You can't use 'macro parameter character #' in math mode סיכום התוצאות בדינמיקה יחסותית: >[!formula] נוסחה: > >$$ > \begin{gather} > p=\gamma mv \\[1ex] > E=\gamma mc^{2} \\[1ex] > E_{k}=mc^{2}(\gamma-1) \\[1ex] > E_{0}=mc^{2} \\[1ex] > p=\sqrt{ \gamma ^{2}-1 } \,\, mc > \end{gather} > $$ ## גודל אינוואריאנטי נשים לב לקשר הבא עבור חלקיק בודד: E^{2}-p^{2}c^{2}=\gamma ^{2}m^{2}c^{4}-\gamma ^{2}m^{2}v^{2}c^{2}=\gamma ^{2}m^{2}c^{4}\left( 1-\dfrac{v^{2}}{c^{2}} \right)=\gamma ^{2}m^{2}c^{4} \frac{1}{\gamma ^{2}}=m^{2}c^{4}
כ ל ו מ ר ה ג ו ד ל ה ו א ק ב ו ע ב נ ו ס ף מ כ י ו ו ן ש מ ס ת ה מ נ ו ח ה ל א ת ל ו י ה ב מ ע ר כ ת ה י י ח ו ס ג ו ד ל ז ה ש ו ו ה ב כ ל מ ע ר כ ו ת ה י י ח ו ס E^{2}-p^{2}c^{2}=E’^{2}-p’^{2}c^{2}=m^{2}c^{4}
ג ו ד ל ש א י נ ו מ ש ת נ ה ב י ן מ ע ר כ ו ת ה י י ח ו ס נ ק ר א ג ו ד ל א י נ ו ו א ר י א נ ט י ד ו ג מ ה פ ר ט י ת ל כ ך ה י א ש ב מ ע ר כ ת מ ר כ ז ה מ ס ה מ ע ר כ ת ש נ ע ה ע ם ה ח ל ק י ק ב מ ק ר ה ז ה ו ל כ ן נ ק ב ל E^{2}-p^{2}c^{2}=E’{\text{com}}{}^{2}-p’ {\text{com}}{}^{2}c^{2}=E’_{\text{com}}{}^{2}=m^{2}c^{4}
ה ג ו ד ל ש י מ ו ש י ל ע י ת י ם ב פ ת י ר ת ב ע י ו ת ב ע ז ר ת ק ש ר ז ה נ ו כ ל ג ם ל ר א ו ת כ י cp=\sqrt{ E^{2}-m^{2}c^{4} }
ו ל כ ן ג ם כ א ש ר ל ג ו ף א י ן מ ס ה ע ד י י ן י ש ל ו ת נ ע p=\frac{E}{c}
ב נ ו ס ף א נ ו י ו ד ע י ם כ י p=\gamma mv,, \quad E=\gamma mc^{2}
ל כ ן \begin{gather}
Erroneous nesting of equation structures מכאן קיבלו שמהירות של חלקיק חסר מסה חייב להיות שווה למהירות האור. >[!notes] הערות: > >1. ראינו שהצירוף $E^{2}-p^{2}c^{2}$ עבור חלקיק יחיד נשאר קבוע במעבר בין מערכות ייחוס שונות. תוצאה זו נכונה גם עבור מערכת סגורה של גופים. במערכת סגורה האנרגיה הכוללת והתנע הכולל נשמרים ומתקיים שהגודל $E_{\text{tot}}^{2}-p_{\text{tot}}^{2}c^{2}$ נשאר קבוע לפני ואחרי התנגשויות\התפרקויות וערכו אינו משתנה במעבר בין מערכות ייחוס. > שימו לב שהגודל של האנרגיה הכוללת והתנע הכולל כן משתנים במעבר בין מערכות ייחוס (הם שמורים רק כאשר מסתכלים על התהליך לפני ואחרי ההתנגשות\התפרקות באותה מערכת ייחוס), אך השילוב הספציפי $E_{\text{tot}}^{2}-p_{\text{tot}}^{2}c^{2}$ נשאר קבוע. >[!example] דוגמה: > > חלקיק בעל מסה $m$ נמצא במנוחה במערכת המעבדה. פוטון בעל אנרגיה $$ > E_{p}=4mc^{2} > $$ מתנגש בחלקיק. > > ![[Pasted image 20230702092725.png|book]] > > > כתוצאה מכך נוצר חלקיק חדש בעל מסה $M$, הנע מרחק $D$ במערכת המעבדה ומתפרק לשני חלקיקים זהים בעלי מסה $m'=\frac{6}{5}m$. החלקיקים שנוצרו נעים לאורך קו התנועה המקורי. > > > ![[Screenshot_20230702_104525_Obsidian.jpg|book]] > > 1. מה המסה $M$? > **פתרון**: > ניקח כמערכת שלנו את הפוטון ואת החלקיק $m$. מכיוון שזו מערכת סגורה, התנע והאנרגיה נשמרים. > אנו מתעניינים במסה של החלקיק שנוצר כתוצאה מההתנגשות של הפוטון וחלקיק $m$. נזכור שמסה זו היא מסת המנוחה של החלקיק (בקורס שלנו, כשנתון מסה של גוף הכוונה היא למסת המנוחה) ולכן יהיה נוח לעבוד במערכת שנעה עם חלקיק $M$ (משום שבמערכת זו חלקיק $M$ במנוחה). הבעיה היא שכל נתוני השאלה הם ביחס למעבדה. > לכן נשתמש בגודל האינוואריאנטי. כאשר המערכת סגורה, התנע והאנרגיה נשמרים, ולכן גודל זה הוא קבוע לפני ואחרי ההתנגשות. בנוסף, מכיוון שהגודל זהה בכל מערכות הייחוס, ניתן להשוות את הגודל לפני ואחרי ההתנגשות במערכות שונות. מכאן שנוכל להשוות את הגודל $E^{2}-p^{2}c^{2}$ לפני ההתנגשות במערכת המעבדה לאותו גודל אחרי ההתנגשות במערכת מרכז המסה של חלקיק $M$: > $$ > \bigg(\underbrace{ 4mc^{2}+mc^{2} }_{ \begin{gather} > \text{Energy before,} \\ > \text{according to the lab} > \end{gather} }\bigg)^{2}-\left( \frac{E_{p}}{c} \right)^{2}c^{2}=M^{2}c^{4}-0 > $$ > במשוואה למעלה השתמשנו בכך שתנע של פוטון הוא $p_{p}=\frac{E_{p}}{c}$ , ובכך שבמערכת מרכז המסה התנע הכולל של המערכת הוא $0$. מכאן נוכל לפתור עבור המסה $M$ כדי לקבל: > $$ > \begin{gather} > 25m^{2}c^{4}-16m^{2}c^{4}=M^{2}c^{4} \\ > M=3m > \end{gather} > $$ > 2. מה מהירות חלקיק $M$ במערכת המעבדה? > **פתרון**: > השאלה מבקשת למצוא את מהירות הגוף במערכת המעבדה. אכן, מכיוון שלמערכת יש תנע לפני ההתנגשות (במערכת המעבדה), אחרי ההתנגשות התנע יהיה זהה. נמצא את המהירות בשתי דרכים שונות: בעזרת שימור אנרגיה ובעזרת שימור תנע. המהירות נכנסת לביטוי של האנרגיה היחסותית דרך פקטור $\gamma$. בעזרת שימור אנרגיה נמצא שבמערכת המעבדה: > $$ > \begin{gather} > 4mc^{2}+mc^{2}=\gamma_{M}Mc^{2} \\ > \gamma_{M}=\dfrac{5mc^{2}}{3mc^{2}}=\frac{5}{3} > \end{gather} > $$ > שימו לב שבמערכת המעבדה לגוף $M$ יש מהירות ולכן האנרגיה שלו היא $\gamma_{M}Mc^{2}$ . מפקטור $\gamma$ נפתור עבור המהירות: > $$ > \begin{gather} > \gamma_{M}=\frac{5}{3}=\frac{1}{\sqrt{ 1-\dfrac{v_{M}^{2}}{c^{2}} }} \\ > v_{M}=0.8c > \end{gather} > $$ > שימו לב שבביטוי לשימור אנרגיה חשוב ששני צידי המשוואה יתייחסו לאותה מערכת ייחוס. במקרה זה בחרנו במערכת המעבדה. רק הגודל האינוואריאנטי אינו משתנה בין מערכות הייחוס. דרך אחרת למצוא את מהירות החלקיק היא בעזרת שימור תנע. לפני ההתנגשות רק לפוטון יש תנע $\frac{E_{p}}{c}$ . מכאן ששימור תנע נותן: > $$ > \begin{gather} > \frac{4mc^{2}}{c}=\sqrt{ \gamma_{M}^{2} -1}\,Mc \\ > \sqrt{ \gamma_{M}^{2}-1 }=\frac{4}{3} \\ > \gamma_{M}=\frac{5}{3} > \end{gather} > $$ > בביטוי זה השתמשנו בקשר $p=\sqrt{ \gamma ^{2}-1 }\,mc$. > 3. נתון ש-$D=\pu{5cm}$. מה זמן החיים $\tau$ (הזמן העצמי) של $M$? > **פתרון**: > השאלה מבקשת למצוא את הזמן שעבר עד שחלקיק $M$ התפרק מבחינת מערכת ייחוס הנעה עם החלקיק. זהו זמן עצמי מכיוון שבמערכת זו החלקיק במנוחה ולכן היווצרותו והתפרקותו התרחשו באותה נקודה במרחב. הקושי בשאלה הוא שכל הפרטים הקינמטים נתונים במערכת ייחוס הקבועה במעבדה. לכן נמצא את זמן ההתפרקות במערכת המעבדה ונתרגם אותה למערכת הנעה עם החלקיק. במערכת המעבדה אנו יודעים שלחלקיק $M$ יש מהירות קבועה $v_{M}$, והוא עבר מרחק $D$ עד שהתפרק. מכאן שנוכל לחשב את הזמן שעבר עד ההתפרקות. בפרט, הזמן במעבדה עד שחלקיק $M$ התפרק הוא $t_{\text{lab}}=\frac{D}{v_{M}}$ . מכאן שהזמן העצמי מקיים את הקשר: > $$ > \begin{gather} > t_{\text{lab}}=\gamma_{M}\tau \\[2ex] > \tau=\dfrac{t_{\text{lab}}}{\gamma_{M}}=\dfrac{0.05}{\frac{5}{3}\times 0.8c}=\pu{1.25\times 10^{-10}s} > \end{gather} > $$ > 4. מה המהירות של החלקיקים הסופיים, $m'$, במערכת המעבדה? > **פתרון**: > לפני ההתפרקות היה לגוף $M$ תנע במערכת המעבדה. מכיוון שהמערכת סגורה, התנע נשמר לפני ואחרי ההתפרקות. מכאן ששני החלקיקים נוצרו עם תנע כל אחד כך שהתנע הכולל נשמר. נוח לעבוד במערכת מרכז המסה של חלקיק $M$ לפני ההתפרקות (במערכת זו החלקיק במנוחה והתנע הכולל במערכת הוא $0$). מכיוון שהחלקיקים שנוצרו זהים והתנע הכולל במערכת מרכז המסה הנ"ל הוא $0$, יש לחלקיקים מהירויות בגודל זהה אך בכיוונים הפוכים (במערכת זו). משיקולים אלה נבצע את החישוב במערכת מרכז המסה של חלקיק $M$. שימו לב שמערכת מרכז המסה של גוף $M$ נעה במהירות יחסית של $v_{M}=0.8c$ ביחס למערכת המעבדה. בעזרת הגודל האינוואריאנטי נקבל: > $$ > \begin{gather} > (3mc^{2})^{2}=\left( 2\gamma' \frac{6}{5}mc^{2} \right)^{2} \\ > (\gamma')^{2}=\frac{225}{144} > \end{gather} > $$ > כאשר בחרנו לקרוא למערכת מרכז המסה $S'$ ולכן מופיע $\gamma'$. נפתור עבור מהירות החלקיקים במערכת מרכז המסה שלהם: > $$ > \begin{gather} > \gamma'=\sqrt{ \frac{225}{144} }=\frac{1}{\sqrt{ 1-\dfrac{(u')^{2}}{c^{2}} }} \\[2ex] > u'=\pm \frac{3}{5}c > \end{gather} > $$ > כאשר $u'$ היא מהירות החלקיקים. כדי למצוא את המהירויות במעבדה, נשתמש בטרנפורמציית לורנץ. אנו מעבירים את המהירויות בין מערכת $S'$ הנעה במהירות $v_{M}=0.8c$ יחסית למערכת המעבדה, $S$: > $$ > \begin{aligned} > &{u}_{1}=\dfrac{{u}_{1}'+v_{M}}{1+\dfrac{v_{M}}{c^{2}}u'_{1}}=\dfrac{0.6c+0.8c}{1+\dfrac{0.8}{c^{2}}0.6c}=0.946c \\[2ex] > &u_{2}=\dfrac{u_{2}'+v_{M}}{1+\dfrac{v_{M}}{c^{2}}u'_{2}}=\dfrac{-0.6c+0.8c}{1+\dfrac{0.8c}{c^{2}}}(-0.6c)=0.385c > \end{aligned} > $$ >[!example] דוגמה: > > חלקיק בעל מסה $M$ נח במעבדה. החלקיק מתפרק לשני חלקיקים זהים, בעלי מסה $m$. כעבור $\Delta t=\pu{10^{-7}s}$ מרגע ההתפרקות, גלאי הממוקם במרחק של $x=18m$ קולט את אחד החלקיקים. מצאו את המסה $m$ כפונקציה של $M$. > ![[Pasted image 20230702093011.png|book]] > **פתרון**: > המערכת סגורה ולכן יש שימור תנע ואנרגיה. נעבוד במערכת המעבדה. לפני ההתפרקות התנע הכולל הוא $0$ ולכן משימור תנע נקבל שהתנע של שני החלקיקים מקיימים: > $$ > \begin{gather} > {p}_{1}+{p}_{2}=0 \\ > {p}_{1}=-{p}_{2} > \end{gather} > $$ > מכיוון שהחלקיקים זהים, מהירותם זהה בגודלה והפוכה בכיוונה. מכאן שיש להם את אותו פקטור $\gamma$. נשתמש כעת בתנאי עבור שימור אנרגיה: > $$ > \begin{gather} > Mc^{2}=2\gamma mc^{2} \\[1ex] > m=\frac{M}{2\gamma} > \end{gather} > $$ > כל שחסר הוא פקטור $\gamma$. נזכור שבמערכת המעבדה אנו יודעים את מהירות החלקיקים: > $$ > u=\frac{\Delta x}{\Delta t}=\dfrac{18}{10^{-7}}=0.6c > $$ > מכאן שפקטור $\gamma$ שלהם (במערכת זו) הוא: > $$ > {\gamma}=\frac{1}{\sqrt{ 1-\dfrac{u^{2}}{c^{2}} }}=\frac{1}{\sqrt{ 1-\dfrac{(0.6c)^{2}}{c^{2}} }}=\frac{5}{4} > $$ > נציב גודל זה לביטוי שמצאנו עבור המסה: > $$ > m=\frac{2}{5}M > $$ >[!example] דוגמה: > > פוטון בעל אנרגיה $E_{p}=E$ הנתונה במערכת המעבדה פוגע בחלקיק נח במערכת המעבדה ומסתו $m=\frac{2E}{c^{2}}$. כתוצאה מכך נבלע הפוטון על ידי החלקיק ונוצר חלקיק חדש בעל מסה $M$. מצאו את $M$. > ![[Pasted image 20230702093109.png|book|300]] > **פתרון**: > המערכת סגורה ולכן יש שימור תנע ואנרגיה. התנע לפני ההתנגשות הוא התנע של הפוטון, $p=\dfrac{E_{p}}{c}$. מכאן שלחלקיק שנוצר יהיה תנע $p=\frac{E_{p}}{c}$ במערכת המעבדה. על מנת לחשב את המסה, יהיה נוח לעבוד במערכת מרכז המסה של החלקיק שנוצר (במערכת זו הוא במנוחה). מכיוון שהפרמטרים בבעיה נתונים במערכת המעבדה, נשתמש בגודל האינוואריאנטי כדי לקשר בין המערכות. > $$ > (E_{p}+mc^{2})^{2}-\left( \frac{E_{p}}{c} \right)^{2}c^{2}=M^{2}c^{4} > $$ > נפתור עבור $M$: > $$ > \begin{gather} > \left( E+\frac{2E}{c^{2}}c^{2} \right)^{2}-\left( \frac{E}{c} \right)^{2}c^{2}=M^{2}c^{4} \\ > 8E^{2}=M^{2}c^{4} \\ > M=\frac{\sqrt{ 8 }E}{c^{2}}=\dfrac{2\sqrt{ 2 }E}{c^{2}} > \end{gather} > $$ > באופן מעניין, $M>m$. הסיבה היא שחלק מאנרגיית הפוטון הפכה למסה. משימור תנע, המסה $M$ חייבת לנוע ביחס למעבדה. נמצא את המהירות משימור אנרגיה. נבצע את החישוב במערכת המעבדה. > $$ > \begin{gather} > E+\frac{2E}{c^{2}}c^{2}=\gamma Mc^{2} \\ > \gamma=\frac{3E}{Mc^{2}}=\dfrac{3E}{\dfrac{2\sqrt{ 2 }E}{c^{2}}c^{2}}=\frac{3}{2\sqrt{ 2 }} > \end{gather} > $$ > כאשר הצבנו את הערך שמצאנו עבור $M$. מכאן נמצא שגודל המהירות היא: > $$ > \begin{gather} > \gamma=\frac{1}{\sqrt{ 1-\dfrac{v^{2}}{c^{2}} }}=\frac{3}{2\sqrt{ 2 }} \\ > 1-\frac{v^{2}}{c^{2}}=\frac{8}{9} \\ > v=\frac{1}{3}c > \end{gather} > $$ > נזכור שמהירות היא וקטור ולכן חשוב לציין עבורה כיוון. משימור תנע אנו יודעים שהמהירות היא בכיוון התנועה של הפוטון. >[!example] דוגמה: > > חלקיק שמסתו $M$, הנע במהירות יחסותית $\vec{v}$ ביחס למערכת המעבדה, מתפרק לשני פוטונים. נתון כי במערכת המעבדה הפוטונים זהים באנרגיה שלהם. מהו הקשר בין מהירות החלקיק לזווית בין הפוטונים? > > ![[Pasted image 20230702093158.png|book|400]] > > **פתרון**: > הפרמטרים בבעיה מוצגים במערכת המעבדה ולכן נעבוד במערכת זו. בעזרת שימור אנרגיה נמצא את אנרגיית הפוטונים כפונקציה של הפרמטרים הנתונים. > $$ > \begin{gather} > \gamma Mc^{2}=2E_{p} \\ > E_{p}=\frac{\gamma Mc^{2}}{2} > \end{gather} > $$ > משימור תנע בכיוון $y$ נקבל: > $$ > 0=\frac{E_{p}}{c}\sin (\theta)-\frac{E_{p}}{c}\sin (\theta)=0 > $$ > כאשר השתמשנו בכך שהתנע של פוטון הוא $p=\frac{E_{p}}{c}$. התנאי עבור שימור תנע בכיוון $y$ לא הוסיפה אינפורמציה. > משימור תנע בכיוון $x$ נקבל: > $$ > \sqrt{ \gamma ^{2}-1 }\,Mc=2 \dfrac{E_{p}}{c}\cos (\theta)=2 \dfrac{ \dfrac{\gamma Mc^{2}}{2}}{c}\cos (\theta)=\gamma Mc \cdot \cos \theta > $$ > נפתור עבור $\cos\theta$: > $$ > \cos (\theta)=\frac{\sqrt{ \gamma ^{2}-1 }}{\gamma}=\sqrt{ 1-\frac{1}{\gamma ^{2}} } > $$ > מכאן אנו רואים שככל שהמהירות של חלקיק $M$ קטנה (כלומר $\gamma$ מתקרב ל-1), $\cos(\theta)$ נהיה קטן (כלומר הזווית נהיית קרובה ל-$\frac{\pi}{2}$). במילים אחרות, ככל שהמהירות קטנה יותר, הזווית גדולה יותר. >[!example] דוגמה: > > חלקיק בעל מסה $M$ מתפרק לשני חלקיקים זהים בעלי מסה $m$. וקטורי התנע של החלקיקים שנוצרו אחרי ההתפרקות הם: > $$ > \begin{aligned} > &\vec{p}_{1}=\frac{1}{2}mc\,\hat{\mathbf{x}}+\frac{\sqrt{ 3 }}{2}mc\,\hat{\mathbf{y}} \\ > &\vec{p}_{2}=\frac{1}{2}mc\,\hat{\mathbf{x}} -\frac{\sqrt{ 3 }}{2}mc\,\hat{\mathbf{y}} > \end{aligned} > $$ > מה מסת החלקיק $M$? > ![[Pasted image 20230702093304.png|book|400]] > **פתרון**: > מכיוון שיש למערכת תנע אחרי ההתפרקות, חייב להיות לחלקיק $M$ תנע גם לפני ההתפרקות. נשים לב שגודל התנע של החלקיקים זהה: > $$ > |{p}_{1}|=|{p}_{2}|=\sqrt{ \left( \frac{1}{2}mc \right)^{2}+\left( \frac{\sqrt{ 3 }}{2}mc \right)^{2} }=mc > $$ > מכאן נמצא את פקטור $\gamma$ שלהם: > $$ > \begin{gather} > p=\sqrt{ \gamma ^{2}-1 }\,mc=mc \\ > \sqrt{ \gamma ^{2}-1 }=1 \\ > \gamma ^{2}=2 \\ > \gamma=\sqrt{ 2 } > \end{gather} > $$ > כאשר השתמשנו בביטוי עבור גודל התנע היחסותי $p=\sqrt{ \gamma ^{2}-1 }\,mc$. > > נשים לב שהתנע הכולל במערכת אחרי ההתנגשות (ומשימור תנע גם לפניה) הוא $\vec{p}=mc\,\hat{\mathbf{x}}$. כדי למצוא את מסת החלקיק $M$, נשתמש בגודל האינוואריאנטי לקשר בין האנרגיה במערכת מרכז המסה שלו לבין התנע והאנרגיה של החלקיקים במערכת המעבדה: > $$ > \begin{gather} > M^{2}c^{4}=(2\cdot\sqrt{ 2 }mc^{2})^{2}-(mc)^{2}c^{2} \\ > M^{2}c^{4}=7m^{2}c^{4} \\ > m=\sqrt{ 7 }M > \end{gather} > $$