אנרגיה פוטנציאלית
אנרגיה פוטנציאלית חד-ממדית
נתחיל מדוגמה:
נתון גוף בעל מסה
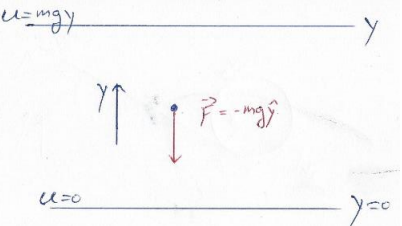
מכיוון שהעבודה תלויה רק בנקודת ההתחלה והסוף של המסלול שעבר הגוף, כוח הגרביטציה הוא כוח משמר. בנוסף, אנו רואים שהעבודה שעשה הגרביטציה פרופורציונית לשינוי האנרגיה הפוטנציאלית.
נצייר גרף של האנרגיה הפוטנציאלית כפונקציה של גובה הגוף. כפי שנראה, גרף זה הוא כלי יעיל בהבנת בעיות בפיסיקה. במקרה של אנרגיה פוטנציאלית גרביטציונית בקרבת כדור הארץ, הגרף ליניארי. אם הגוף מתחיל בנקודה
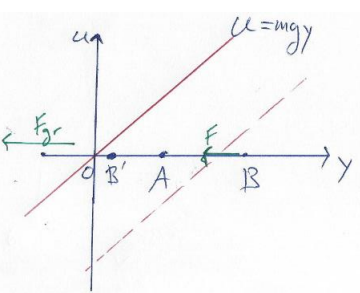
נעבור נעבור מגרביטציה לקפיץ. נדון במסה המחוברת לקפיץ. כפי שראינו בכוח משמר, האנרגיה הפוטנציאלית של הקפיץ נתונה כ-
נהוג להגדיר את האפס של האנרגיה הפוטנציאלית של הקפיץ במרחק המנוחה
נצייר גרף של האנרגיה הפוטנציאלית של הקפיץ כפונקציה של אורך המתיחה.
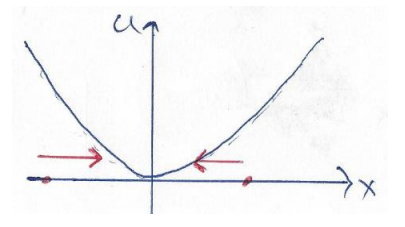
מכיוון ש-
באופן כללי, אם נשחרר גוף בנקודה כלשהי ממנוחה, הגוף ינוע במורד האנרגיה הפוטנציאלית. מדוגמאות אלו אנו רואים שאם אנו יודעים את הכוח המשמר הפועל על המערכת, במקרה זה כוח הקפיץ ובמקרה הקודם כוח הגרביטציה, אנחנו מסוגלים לחשב את האנרגיה הפוטנציאלית. גם הדרך ההפוכה אפשרית, כלומר אם אנו יודעים את האנרגיה הפוטנציאלית אפשר למצוא בעזרתה את הכוח.
נתחיל במקרה של הקפיץ:
כאשר השוויון האחרון מתקבל משום שכוח הקפיץ הוא
סימן המינוס אומר שהכוח מצביע נגד כיוון גדילת הפוטנציאל, כפי שדיברנו עד כה. אז עבור קפיץ, ניתן למצוא את הכוח מהאנרגיה הפוטנציאלית באמצעות גזירה והוספת סימן מינוס.
עבור גרביטציה בקרבת כדור הארץ,
ניתן להוכיח שעבור כוח משמר, ניתן להגדיר עבורו פונקציית אנרגיה פוטנציאלית
נסיק כי:
משפט:
עבור כוח משמר (ורק עבור כוח משמר) ניתן להגדיר פונקציית פוטנציאל כך ש:
אנרגיה פוטנציאלית תלת מימדית
במקרה התלת ממדי, אם אנו יודעים את האנרגיה הפוטנציאלית כפונקציה של הקואורדינטות
כאשר:
קיבלנו למעשה שוקטור הכוח הוא הגרדיאנט של פונקציית הפוטנציאל:
משפט:
לכל כוח משמר (ורק לכח משמר)
קיימת פונקציית פוטנציאל כך ש: כאשר עדיין מתקיים:
נקודות שיווי משקל
נניח כעת שאנו דנים בגוף הנע בתוך הפוטנציאל החד-ממדי שמופיע באיור למטה. בפוטנציאל זה יש נקודות בהן
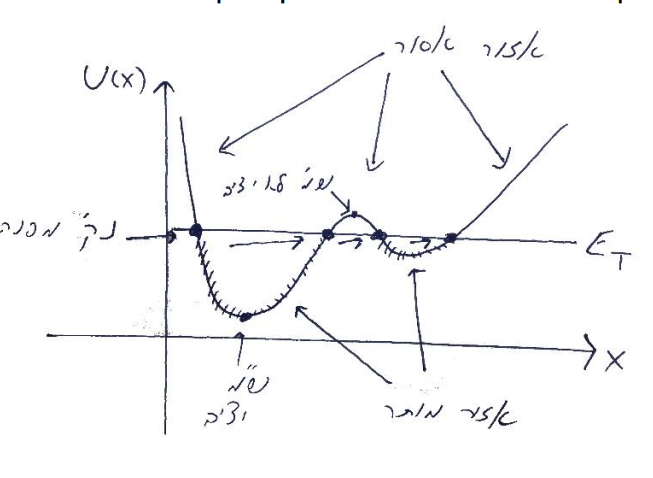
יש הבדל גדול בין נקודות המקסימום לנקודות המינימום של פונקציית הפוטנציאל. אם נניח גוף בנקודת המקסימום, כל סטייה קטנה ממקום זה תגרום לגוף להרגיש כוח ולזוז במורד האנרגיה הפוטנציאלית. בנקודות המינימום, לעומת זאת, סטיות קטנות יגרמו לגוף לחזור לכיוון נקודת המינימום של האנרגיה הפוטנציאלית, כי הכוח תמיד פועל נגד כיוון עליית הפוטנציאל.
אנו קוראים לנקודות המינימום של האנרגיה הפוטנציאלית נקודות שיווי משקל יציב. עבור נקודות אלו מתקיימים שני התנאים:
אנו קוראים לנקודות המקסימום נקודות שיווי משקל לא יציב. עבור נקודות אלו מתקיימים שני התנאים:
אם הנגזרת השנייה שווה לאפס,
שיווי משקל יציב:
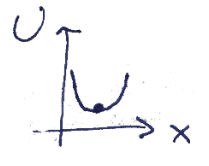
שיווי משקל לא יציב:
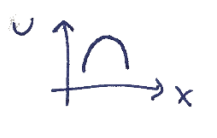
שיווי משקל רופף:
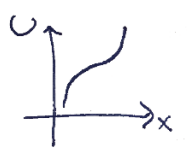
שיווי משקל אדיש:

נקודות מפנה
עבור מקרים שבהם פועלים על גוף רק כוחות משמרים, האנרגיה מכנית קבועה. מכיוון שהאנרגיה הקינטית לעולם לא שלילית, תמיד חייב להתקיים שהאנרגיה הפוטנציאלית תהיה קטנה מהאנרגיה הכוללת:
מכאן שהגוף לא יגיע לעולם למקום בו האנרגיה הפוטנציאלית גדולה מהאנרגיה הכללית.
בדוגמא שלנו, הגוף לא יכול להימצא במקומות איפה שהאנרגיה הפוטנציאלית גדולה מסך האנרגיה ההתחלתית,
נמחיש זאת ע”י קפיץ:
ראינו כי מסת הקפיץ עושה תנודות הרמוניות המתאורות ע”י משוואת התנועה:
פתרון משוואה זו:
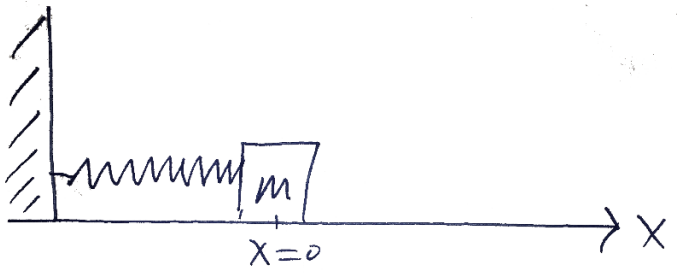
כעת ניתן לשאול, עבור זמן אקראי
אכן האנרגיה המכנית היא קבועה ללא תלות בזמן או במקום הגוף. במהלך התנודות, האנרגיה הקינטית הופכת לפוטנציאלית (ולהפך) בדיוק באופן על מנת ששימור אנרגיה תתקיים. בנוסף, אנו רואים שהאנרגיה המכנית שווה לאנרגיה הפוטנציאלית של הקפיץ כאשר המסה נמצאת ב-

- עבור
:
הגוף במנוחה רגעית וכל האנרגיה היא פוטנציאלית. - עבור
:
הקפיץ רפוי וכל האנרגיה היא קינטית. בנקודה זו מהירות הגוף מקסימלית. - עבור
.
כאן האנרגיה היא שילוב של אנרגיה קינטית ופוטנציאלית.
עבודת כוחות לא משמרים
ממשפט העבודה אנרגיה, העבודה הנעשית על ידי שקול הכוחות במערכת שווה לשינוי באנרגיה הקינטית. נדגיש ששקול הכוחות כולל בתוכו גם את הכוחות המשמרים וגם את הכוחות הלא משמרים.
נחלק את העבודה של שקול הכוחות לסכום של עבודת הכוחות המשמרים ולעבודת הכוחות הלא משמרים. מכאן ש:
העבודה של הכוחות המשמרים היא:
נציב את זה בביטוי של משפט העבודה אנרגיה ונקבל:
משפט:
כלומר, השינוי באנרגיה המכנית הכוללת שווה לעבודה של הכוחות הלא משמרים (אם כל הכוחות בבעיה משמרים, אין שינוי באנרגיה המכנית הכוללת).