ICT1_HW001 פרויקטון 1

	סטודנט א’	סטודנט ב’
שם	עידו פנג בנטוב	יובל הנדל
ת”ז	322869140	211828587
דואר אלקטרוני	ido.fang@campus.technion.ac.il	yuval.hendel@campus.technion.ac.il

קוד MATLAB נמצא בGitHub.

---

---

חלק א’

שאלה 1

ללא הזנחת השראות, המשוואת מנוע DC:

כאשר הוא המתח כניסה, הוא מתח הכא”מ החוזר, הוא התנגדות המנוע, הוא הזרם, ו- הוא השראות המנוע.
נחלק ב-:

בהזנחת ההשראות נקבל:

מתח הכא”מ החוזר הוא:

כאשר הוא קבוע הכא”מ החוזר. לכן:

נכפול בקבוע מנוע :

הביטוי בצד שמאל הוא למעשה המומנט שהמנוע מפעיל:

במישור לפלס:

נתון כי הגלגל שיניים מגדיל את המומנט הנוצר ע”י המנוע לפי:

בנוסף, נתון כי דינמיקת העומס מתוארת ע”י:

נציב את כל המשוואות אחת בשנייה כדי לקבל את המשוואה הבאה עבור זווית זרוע המנוע. מהצבת ב-:

נציב את :

---

---

במישור לפלס:

נוכל כעת לבנות את הדיאגרמת בלוקים:

דיאגרמת בלוקים של המערכת הנתונה.

שאלה 2

מהדיאגרמת בלוקים, וכללי פישוט דיאגרמות:

נישאר עם:

באותו אופן עבור :

נרצה להציג את הפונקציית תמסורת בצורה הבאה:

נמצא כי:

כאשר הוא ההגבר הסטטי ו- הוא קבוע הזמן.

שאלה 3

ניתן לראות מ- ש- הוא proper ויש לו קוטב ב-LHP הפתוח (כל הקבועים חיוביים), ולכן הוא יציב.
עבור , ממשוואה , יש קוטב , ולכן הוא לא יציב.

חלק ב’

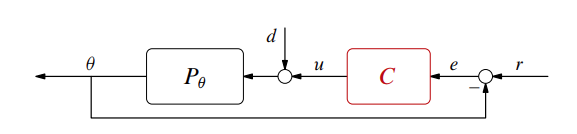
נתונים:

שאלה 4

סעיף א’

עבור וה- שקיבלנו:

הייצוג מג”ש:

לכן הקטבים בחוג הפתוח:

---

---

• עבור :
  מאחר ויש מספר אי זוגי של שורשים מימין, בין ו-, נסיק כי יש ענף על הציר הממשי, בין ל-. בנוסף, יש עודף של שני קטבים, ולכן ישנם שתי אסימפטוטות בזוויות .
  

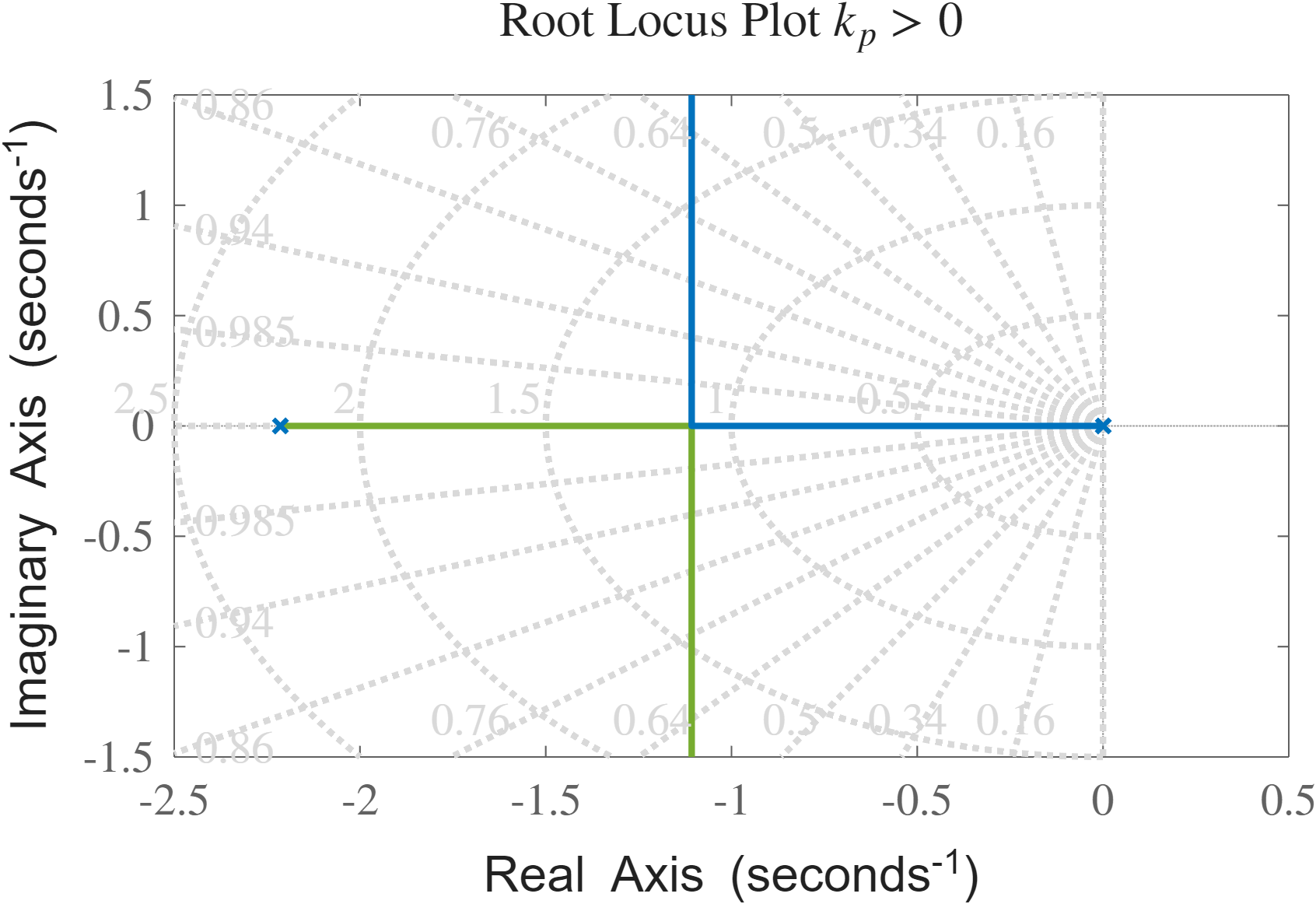
  מג”ש המערכת עבור .

  נסיק שהמערכת יציבה עבור כל .

• עבור :
  מאחר ויש מספר זוגי של שורשים מימין ל- ומשמאל ל- נסיק כי יש ענף על הציר הממשי מימין ל- ומשמאל ל-. בנוסף, יש עודף של שני קטבים, ולכן ישנם שתי אסימפטוטות בזוויות .
  

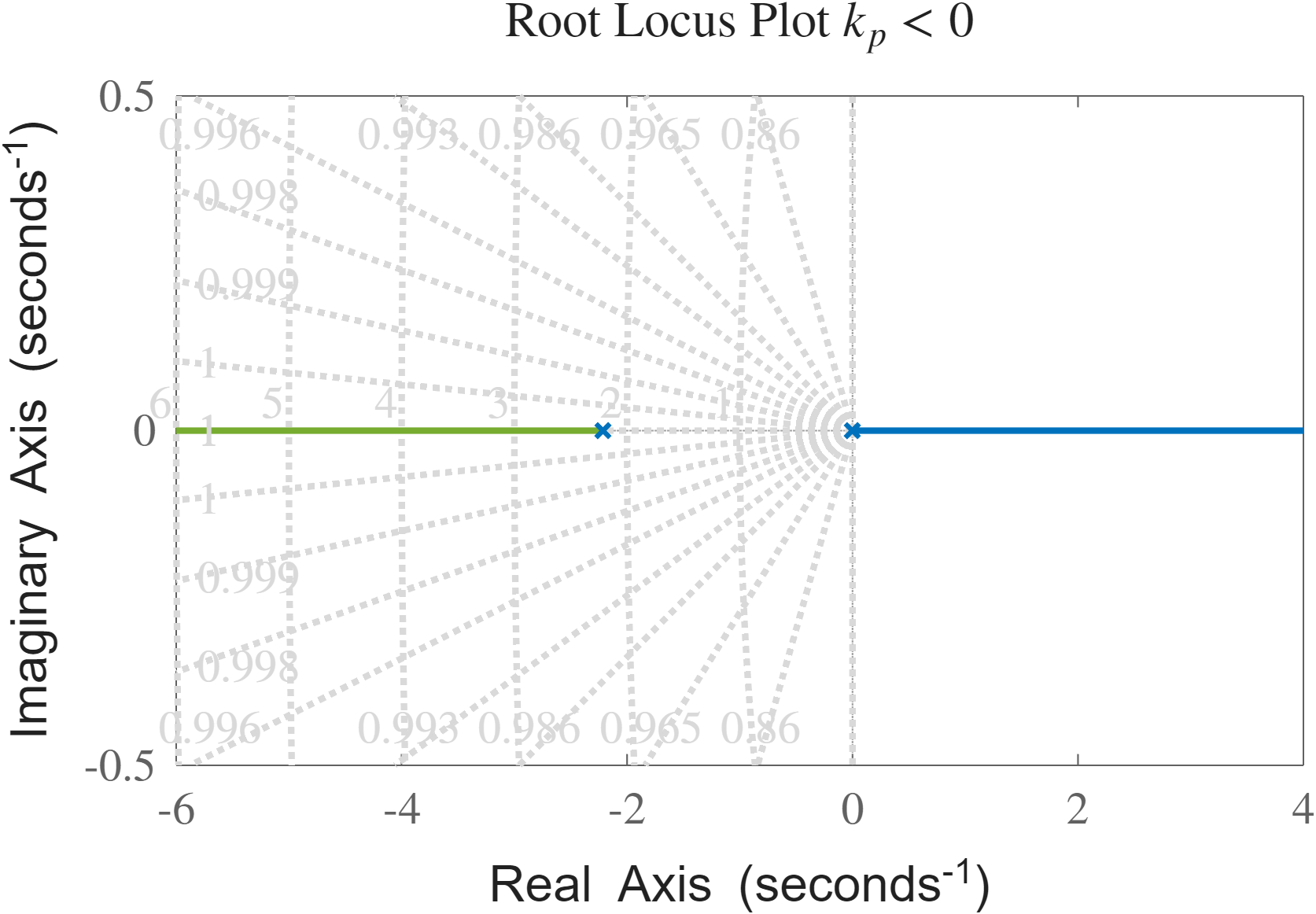
  מג”ש המערכת עבור .

  נסיק שהמערכת לא יציבה עבור כל .

---

---

סעיף ב’

ראינו בהרצאה שהשגיאה עבור אות ייחוס מדרגה מתאפסת כאשר:

במקרה שלנו:

בהינתן ו- , שזה נכון עבור כל בקר המייצב את המערכת.
נסיק ש- אמ”ם מייצב את המערכת, שזה נכון עבור המקרה שלנו ש- לכל .

סעיף ג’

מערכת כללית מסדר שני היא מהצורה:

שלושת פונקציות התמסורת של החוג הסגור הן:

לכולם אותו המכנה, שהוא הפולינום האופייני:

לכן, כאשר נרצה להתאים את המערכות שלנו לצורה , נקבל שהתדירות הטבעית היא:

ולכן מקדם הריסון:

נבודד את :

נציב נתונים ונקבל שערכי עבורם נקבל מקדמי ריסון הם:

לגבי , במקרה של מערכת מסדר שני אנו יודעים ש:

ולכן נקבל שבטווח :

סעיף ד’

ממשוואה :

נבודד את :

ולכן נקבל עבור:

סעיף ה’

לפי שגיאה עבור הפרעת מדרגה, השגיאה במצב מתמיד היא:

כאשר נעלם לנו כי . במקרה הנתון, , ורוצים ש- , ולכן נדרוש ש- . במילים אחרות:

לגבי הטווח , ראינו במשוואה ש:

ולכן טווח ה- הוא:

כך שה-, לפי , הוא:

שאלה 5

סעיף א’

עבור הבקר , נבנה את הייצוג מג”ש:

יש לנו אפס אחד ב- , ושלושה קטבים, שניים מהם על הראשית , והשלישי ב- . לכן, נקבל דיאגרמות שונות כתלות במיקום יחסית ל-. כלומר, נפרק למקרים הבאים:

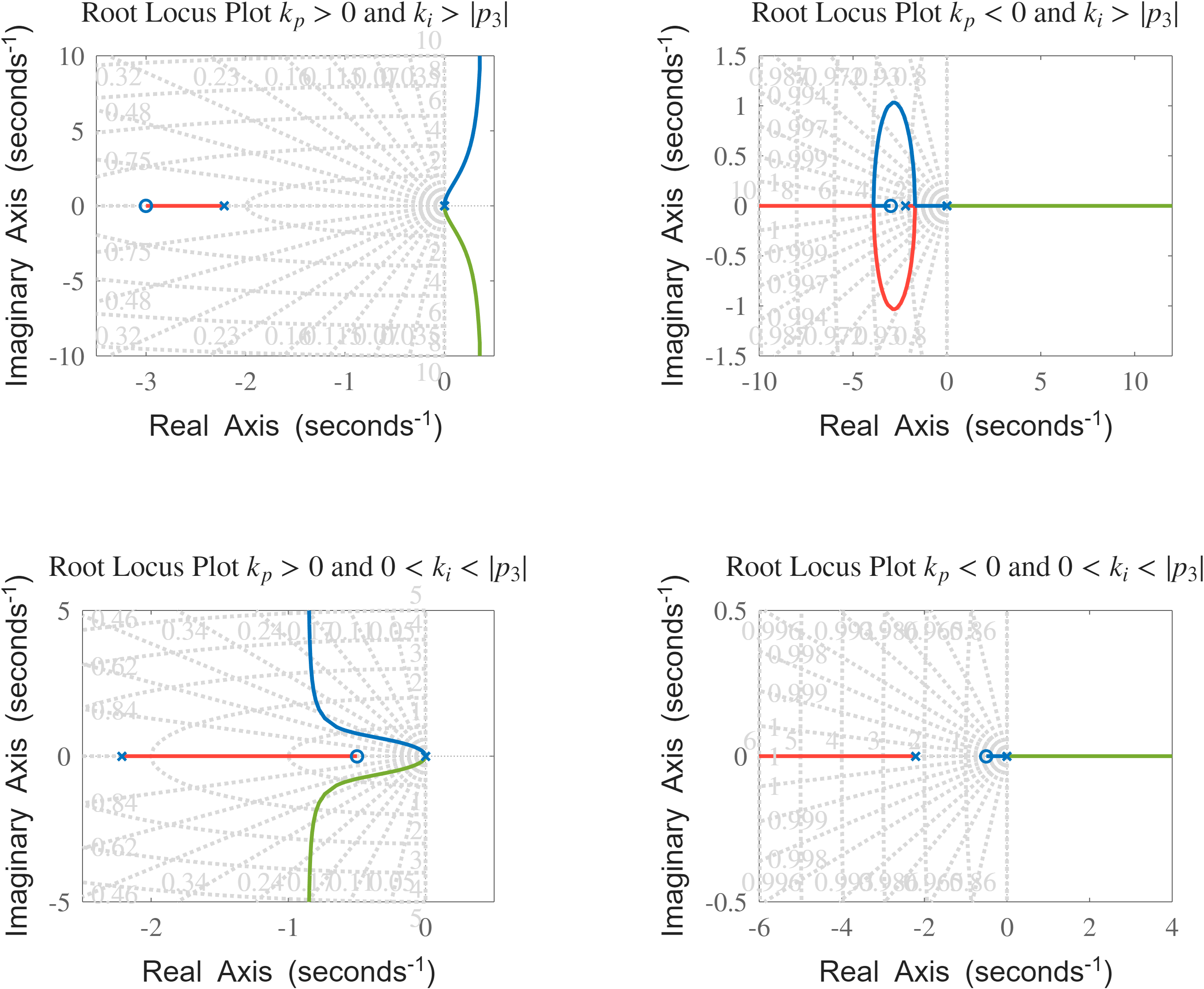
דיאגרמת מג”ש עבור ערכי ו- שונים. לא נתייחס למקרה של כי ניתן לראות שהמערכת לא תהיה יציבה אם יהיה אפס ב-RHP. במקרה של , נקבל בדיוק את אותו הבקר משאלה 4.

קיבלנו שהמערכת תהיה יציבה רק אם:

סעיף ב’

כפי [[#שאלה 4#סעיף ב’|שאלה 4 סעיף ב’]], ראינו שנקבל עבור כל שמייצג את המערכת, או פשוט:

שזה נכון עבור המקרה שלנו ש- עבור כל:

סעיף ג’

באותו אופן כמו [[#שאלה 4#סעיף ה’|שאלה 4 סעיף ה’]], נדרוש ש- . במילים אחרות:

המכנה שואף לאינסוף, ולכן התנאי לעיל מתקיים עבור כל ו-. מאחר ודרוש גם מערכת יציבה, נדרוש ש:

סעיף ד’

עבור הרצת ערכי ו- שונים קיבלנו שעבור כניסת מדרגה, לפונקציית התמסורת :

Best kp: 0.37748
Best ki: 0.01
Best Overshoot: 14.7704
Best Settling Time: 2.8092

תגובת המדרגה היא:

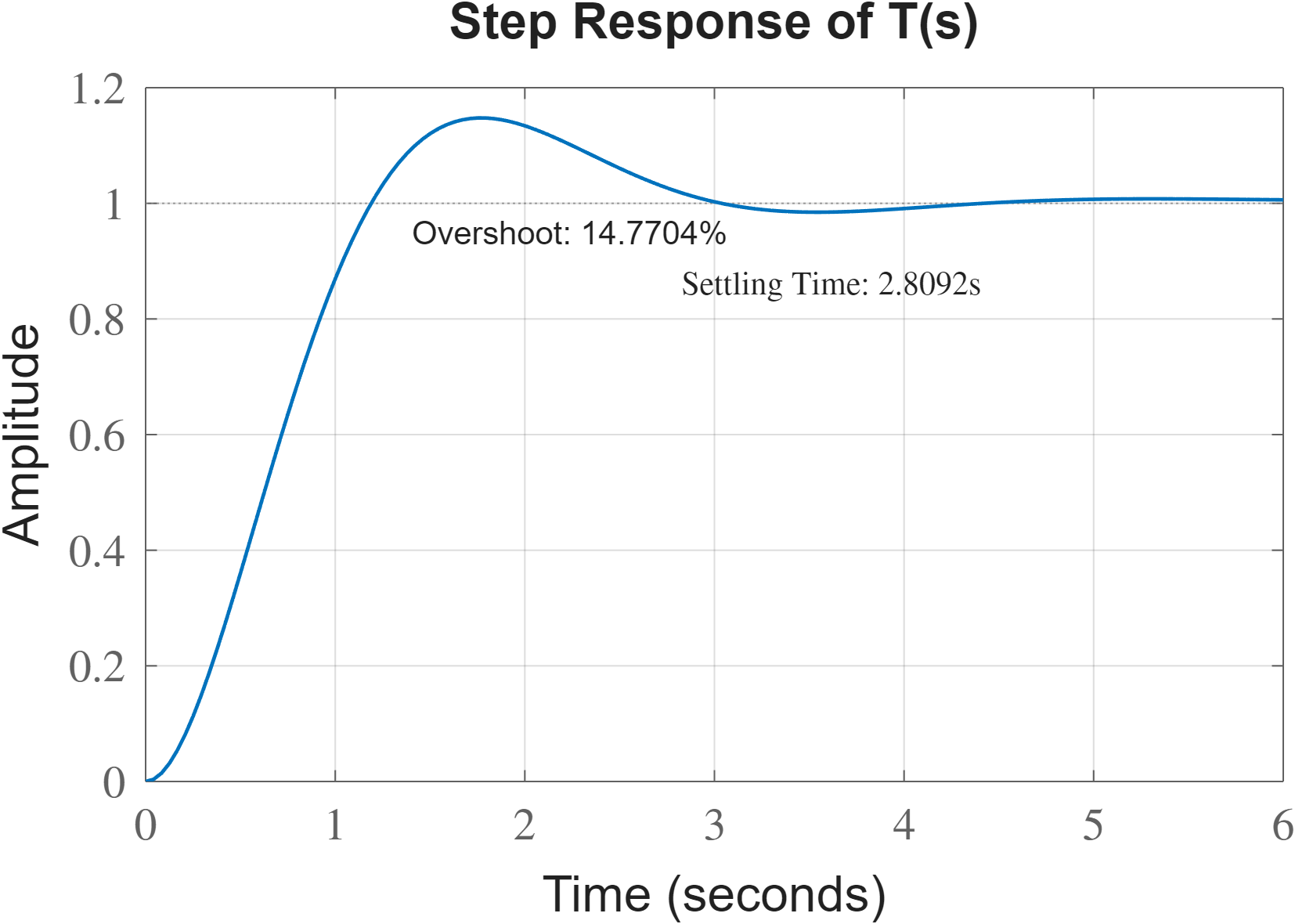
תגובת המדרגה של .