FLD1_HW006 תרגיל בית 6

שאלה 1

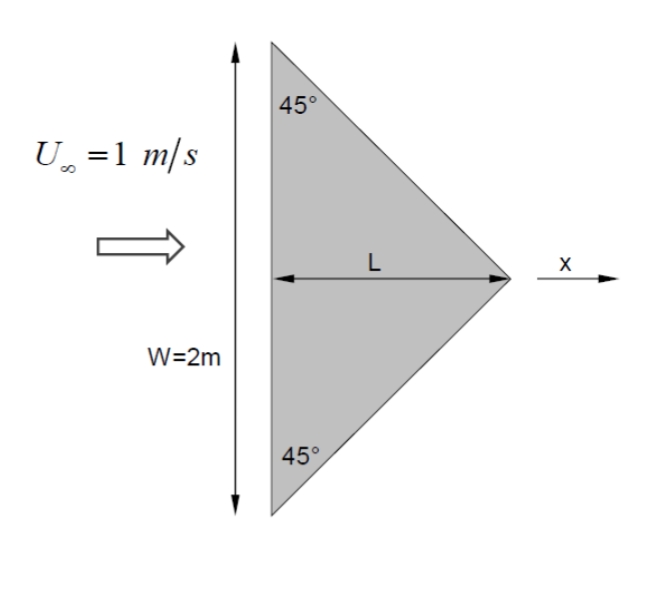
סכימת הפלטה

סעיף א’

לפי בלסויס:

לכן, על הפלטה כוח הגרר (משני הצדדים) יהיה:

מגאומטרית הפלטה, נסיק שהקשר בין רוחב הפלטה ל- הוא:

ולכן גבולות האינטגרציה שלנו הן:

נשים לב גם ש- , ולכן:

סעיף ב’

נגדיר:

נשים לב ש:

לפי תנאי שפה על שכבות גבול:

עבור תנאי השפה השלישי, אנו יודעים ש- . מאחר ו- , נוכל לומר כי:

לפי כלל השרשרת:

נסיק ש:

ולכן . נסכם:

סעיף ג’

לפי אינטגרל פון קרמן:

נחשב את העובי שכבת מומנטום:

מאחר ו- , נסיק כי . נציב באינטגרל פון קרמן:

אנו גם יודעים מהגדרת המאמץ על הקיר ש:

נשווה בין שני הערכים של שקיבלנו:

קיבלנו משוואה פרידה. נבצע אינטגרציה:

סעיף ד’

מסעיף קודם:

נציב את שקיבלנו:

סעיף ה’

נציב את החדש באותם החישובים מ[[#שאלה 1#סעיף א’|סעיף א’]] ונקבל:

סעיף ו’

השגיאה היחסית מוגדרת כ:

שאלה 2

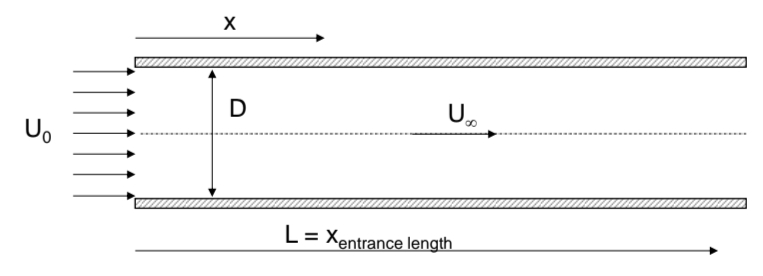
סעיף א’

לפי הגדרת עובי שכבת מומנטום:

נציב את הנתון:

ולכן:

סעיף ב’

באותו אופן כמו ב[[FLD1_009 שכבות גבול#שאלה 2#סעיף א’|שאלה מתרגול]], נסיק שבאורך הכניסה מתקיים .
מאינטגרל פון קרמן אנו יודעים ש:

מהגדרת מאמץ הגזירה בקיר אנו גם יודעים ש:

נשווה:

נציב ערכים שאנו מכירים:

זוהי משוואה פרידה. נבצע אינטגרציה:

נציב בחזרה בתנאי ש:

סעיף ג’

נבצע שימור מסה אינטגרלי על הכניסה והיציאה מהתעלה:

בסוף התעלה אנו יודעים שעובי שכבת הגבול הוא כבר . נציב: