| סטודנט א’ | סטודנט ב’ | |
|---|---|---|
| שם | עידו פנג בנטוב | ניר קרל |
| ת”ז | 322869140 | 322437203 |
| דואר אלקטרוני | ido.fang@campus.technion.ac.il | nir.karl@campus.technion.ac.il |
תרגיל 1
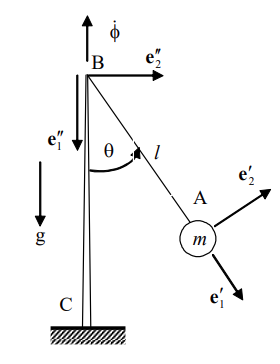
סכימת המטוטלת
סעיף א’+ב’
אין משמעות לשימור תנע זוויתי וקווי בכיוון
כך שלא מתקיים שימור תנע זוויתי ביחס לנקודה
סעיף ג’
נחשב את סך המומנטים ביחס לנקודה
לכן, לפי מאזן תנע זוויתי:
בכיוון
כך שמתקיים שימור תנע זוויתי ביחס לנקודה
סעיף ד’
דג”ח על המסה
החוט מפעיל כוח
נסיק כי החוט לא מבצע עבודה על המסה.
סעיף ה’
מהגדרת התנע הזוויתי:
ברגע ההתחלתי, נתון ש-
מאחר ומתקיים שימור תנע זוויתי ביחס, נוכל לקבוע כי תמיד:
סעיף ו’
נרצה למצוא ביטוי ל-
נשים לב גם שסיבוב מערכת הצירים
לכן, לפי כלל האופרטור:
| נקבל: |
לכן האנרגיה הקינטית:
לסיכום:
סעיף ז’
מהגדרת התנע הזוויתי, אנו יודעים ש:
נציב את הביטוי ל-
מ[[#שאלה 1#סעיף ה’|סעיף ה’]] אנו מצאנו עוד ביטוי ל-
סעיף ח’
הכוח היחיד שמבצע עבודה הוא כוח הכבידה, כך שנוכל להשתמש בשימור אנרגיה:
בכללי, האנרגיה הקינטית והפוטנציאלית (אנרגיה קינטית כבר מצאנו, פוטנציאלית נגדיר
נשווה ביחס לאנרגיות ברגע ההתחלה:
סעיף ט’
דג”ח על המסה
נבצע מאזן תנע קווי:
ולכן:
סעיף י’
מצאנו כי:
נגזור לפי כלל האופרטור:
ממאזן תנע קווי בכיוון
נציב את
תרגיל 2
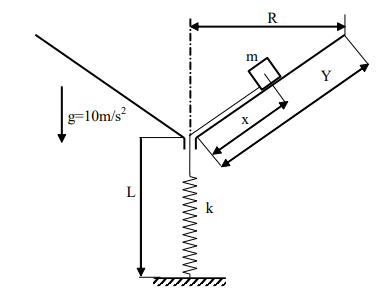
סכימת החלקיקים
סעיף א’
דג”ח על המסה ובחירת מערכת הצירים בתחתית הקונוס
הכוחות שפועלים על המסה הם כוחות משמרים (כוח כבידה, קפיץ) וכוח שלא מבצע עבודה (כוח נורמלי) כי הוא ניצב לתנועת המסה. לפיכך, מתקיים שימור אנרגיה:
גיאומטריית המצב בזמן במרחק
כללי
נשים לב ש:
ולכן, גובה החלקיק (ביחס לקצה התחתון של הקונוס) הוא:
נציב ביחד עם נתונים ידועים:
נרצה כעת למצוא את
מבט על החלקיק
נשים לב שבכיוון
בכל זמן נתון. לפיכך, מתקיים שימור תנע זוויתי בכיוון
מהגדרת התנע הזוויתי:
מיקום ומהירות החלקיק (במערכת קואורדינטות
נציב:
ולכן:
ומשימור תנע זוויתי:
מהנתונים,
לכן:
נציב בחזרה בשימור אנרגיה, ביחד עם הפרמטרים:
סעיף ב’
כדי למצוא את ה-
(שאר הפתרונות לא פיזיקליים).
נסיק ש-
סעיף ג’
בסעיף קודם מצאנו ש:
מאחר וזהו הרכיב היחיד של המהירות, נוכל להסיק ש:
נציב נתונים ונקבל:
תרגיל 3
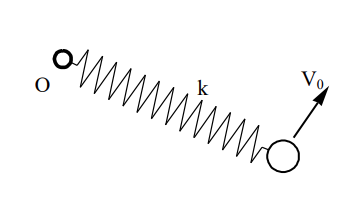
סכימת המסה והקפיץ
סעיף א’
דג”ח על המסה
מאחר והמסה לא זזה בכיוון האנכי, נסיק ש-
מבחינת תנע זוויתי, הוא נשמר בכל הכיוונים, כי כל הכוחות או מתאפסים אחד מול השני (כבידה ונורמל), או שעוברים דרך הנקודה הקבועה
במערכת ישנם רק כוחות משמרים (קפיץ וכבידה) וכוחות שלא מבצעים עבודה (כוח נורמלי), כך שגם מתקיים שימור אנרגיה כוללת.
סעיף ב’
המסה מבצעת תנועה מעגלית ברדיוס משתנה (באופן הרמוני, בגלל הקפיץ). כיוון שמתקיים שימור תנע זוויתי בכיוון האנכי, כאשר הרדיוס גדול המסה תנוע לאט ביחס למהירותה כאשר הרדיוס קטן.
תרגיל 4
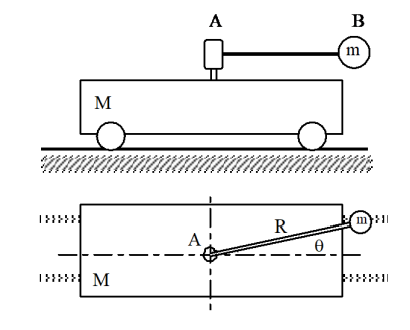
סכימת העגלה
סעיף א’
דג”ח על כלל מערכת החלקיקים
מהדג”ח ניתן לראות שלא פועלים כוחות חיצוניים בכיוון
התנע הזוויתי של מערכת חלקיקים מוגדר כ:
כאשר
נשים לב ש-
ולכן המהירות (גזירה פשוטה, לא צריך כלל האופרטור):
נציב בהגדרת התנע הקווי של המערכת:
לכן, לפי שימור תנע קווי בכיוון
בין אם
אנו יודעים ש:
נציב ונקבל:
סעיף ב’
הערה:
ממבט ראשון נרצה כנראה להשתמש בשימור תנע זוויתי של המסה סביב
, כי אין מומנטים סביב נקודה . הבעיה שאי אפשר להשתמש בתנע זוויתי מוחלט, כי היא נקודה שזזה (מאיצה אפילו). נוכל להשתמש במקום בשימור תנע זוויתי יחסי ל- , אבל כשקלטתי את זה ,כבר ויתרתי על שימור תנע זוויתי, ועברתי לשימור אנרגיה.
נשים לב שהכוחות היחידים שמבצעים עבודה במערכת הם כוחות משמרים (הכוחות הנורמליים והכוחות הציריים ניצבים תמיד לכיוון התנועה ולכן עבודתם אפסית). נסיק כי מתקיים שימור אנרגיה במערכת:
נשים לב ש:
מ[[#תרגיל 4#סעיף א’|סעיף א’]] (שימור תנע קווי) נוכל למצוא ביטוי כללי ל-
נציב בחזרה בביטוי ל-
בנוסף, הכבידה לא מבצעת עבודה, ולכן
לכן, כאשר
סעיף ג’
מהביטוי ל-
כאשר
סעיף ד’
נביט בביטוי שפיתחנו עבור
נקבל ערך מינימלי עבור