CAL2_009 פונקציות סתומות

הערות:

כל הגדרה כאן ניתן בקלות להרחיב לפונקציה ב- משתנים.

פונקציות סתומות

ציטוט מנאדר:

סטודנט: “נאדר מה הנושא הבא?”
נאדר: “סתומות יא חביבי !!!”

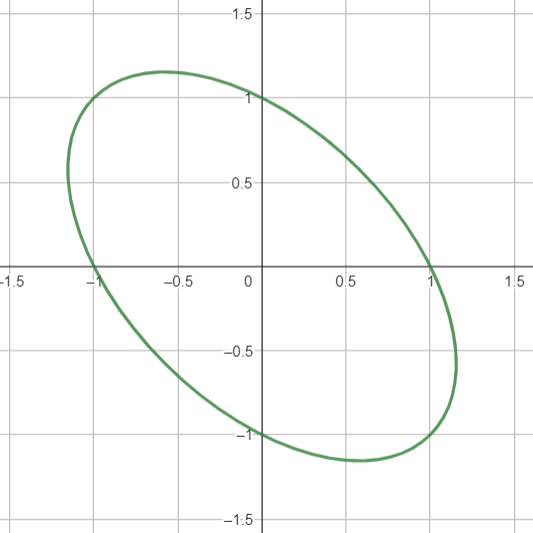
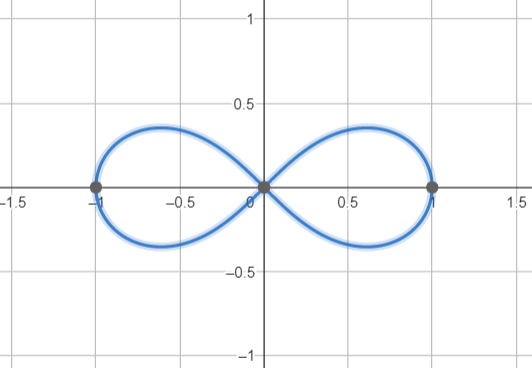
נניח ויש לנו פונקציה ואנו מעוניינים בפתרונות המשוואה . למשל:

נביט בקו גובה:

נטיל את קו גובה זה על מישור :

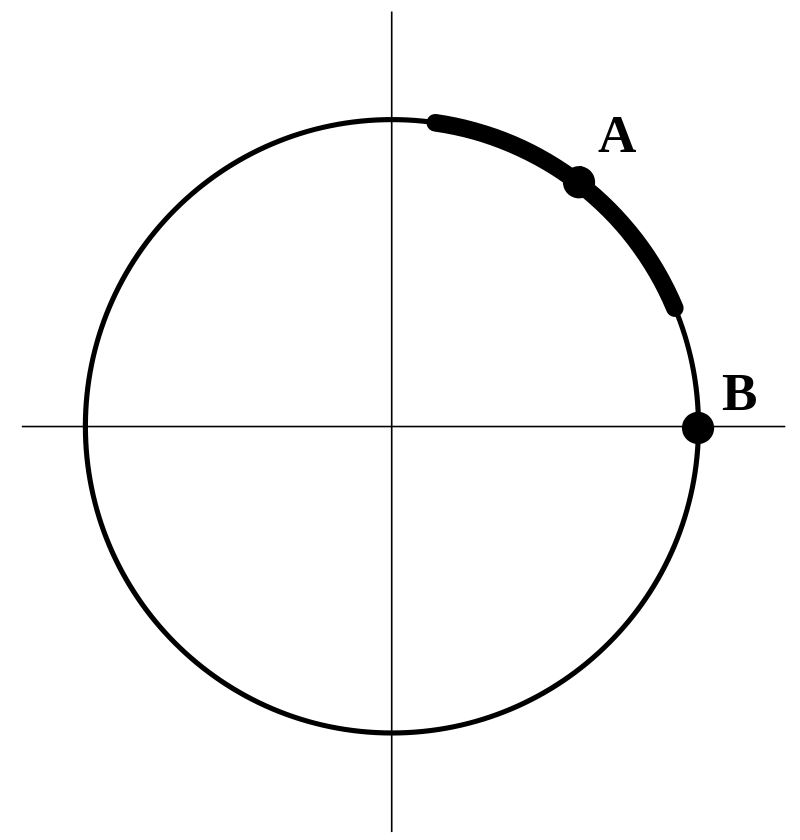
לא ניתן לייצג את קו גובה זה כגרף של פונקציה במשתנה אחד - הרי עבור כל בחירה של , ישנם שתי בחירות עבור :

אבל, עדיין ניתן לייצג חלק מהמעגל כגרף של פונקציה במשתנה אחד. אם נסמן:

אז הגרף של מתאר את החלק העליון של המעגל. באותו אופן:

מתאר את החלק התחתון של המעגל.

לסיכום, נוכל לומר כי הפונקציות הן פונקציות מפורשות שנותנות את אותו הקשר בין ו- כמו במשוואה:

טענה זו נכונה לסביבה של כל נקודה, חוץ מהנקודות . בסביבת נקודות אלו לא ניתן לחלץ פונקציה מפורשת שתקיים את המשוואה.

משפט הפונקציות הסתומות נותן לנו תנאים, תחתם ניתן לחלץ אפילו מפונקציה הנתונה ע”י משוואה סתומה מהסוג:

פונקציה מפורשת בסביבה של נקודה מסוימת.

פונקציה סתומה

הגדרה:

משוואה סתומה היא משוואה מהצורה:

כאשר הוא פונקציה של מספר משתנים.
פונקציה סתומה מוגדרת ע”י משוואה סתומה, בהקשר לאחד מן המשתנים במשוואה, ומשתנה זה נחשב ערך הפונקציה, כאשר האחרים הם המשתנים שלה.

הערות:

1. ישנם פונקציות סתומות שניתן לכתוב אותן כפונקציות מפורשות, כלומר מהצורה הלא סתומה:

אבל, ישנן פונקציות, כמו בדוגמאות, שעבורן זה לא ניתן עבור נקודות מסוימות.

דוגמאות:

1. המשוואה הסתומה הבאה:

מגדירה פונקציה סתומה, אבל לא ניתן להציג אותה בצורה מפורשת של .

1. מהמשוואה הסתומה הבאה:

לא ניתן לחלץ פונקציות מפורשות בסביבת הנקודה .

משפט הפונקציות הסתומות לשני משתנים

משפט:

תהי הפונקציה המוגדרת בסביבת הנקודה ככה ש:

1. מתקיים .
2. הפונקציה בעלת נגזרות חלקיות רציפות בנקודה ובסביבתה.
3. הנגזרת החלקית לפי מקיימת: .

אזי קיימת סביבה של שבה המשוואה מגדירה פונקציה יחידה , ועבורה:

1. מתקיים .
2. לכל בסביבת מתקיים .
3. ה- גזירה ברציפות בסביבת-, ומתקיים:

דוגמאות:

1. נתונה הפונקציה:

האם בסביבת הנקודה , המשוואה: מקיימת את תנאי המשפט?
נבדוק שאכן הנקודה נמצאת על העקומה:

נבדוק את תנאי המשפט.
אלמנטרית עם נגזרות חלקיות רציפות בכל המישור.

קיימת כאשר והיא גזירה בנקודה , ומתקיים:

ישר המשיק לקו גובה

משפט:

יהי קו גובה של המתאים לנקודה . כלומר . נניח:

1. הנגזרות החלקיות רציפות ב-.
2. מתקיים .

אז בנקודה קיים ישר משיק לקו הגובה בנקודה ומשוואתו היא:

הערות:

1. משוואה זו תואמת למשפט שהגרדיאנט הוא נורמל לקו גובה. הרי כיוון הגרדיאנט הוא , וכיוון הישר שקיבלנו במשפט זה הוא . ואכן מכפלתם הסקלרית היא .

משפט הפונקציות הסתומות לשלושה משתנים

משפט:

תהי הפונקציה המוגדרת בסביבת הנקודה ככה ש:

1. מתקיים .
2. הפונקציה בעלת נגזרות חלקיות רציפות בנקודה ובסביבתה.
3. הנגזרת החלקית לפי מקיימת: .

אזי קיימת סביבה של שבה המשוואה מגדירה פונקציה יחידה , ועבורה:

1. מתקיים .
2. לכל בסביבת מתקיים .
3. ה- גזירה ברציפות בסביבת , ומתקיים:

תרגילים:

1. נתונה המשוואה: האם מוגדרת באופן יחיד בסביבת ? כנ”ל לגבי . אם כן, חשבו נ”ח לפי .
   פתרון:
   הפונקציה שלנו: אכן מתקיים התנאי הראשון למשפט הפונקציות הסתומות: התנאי השני:
   בעלת נ”ח בסביבת הנקודה, כי היא מורכבת מפולינום, אקספוננט ו- שגזירה ברציפות בסביבת .
   התנאי השלישי: נסיק כי מוגדרת באופן יחיד בסביבת הנקודה. נחשב נגזרות חלקיות: ניתן לגזור גם ע”פ כללי הגזירה: נציב :
2. הראו כי המשוואה: מגדירה פונקציה יחידה המוגדרת בסביבת: והמקיימת .
   בנוסף, ראשמו פולינום טיילור מסדר ראשון לפונקציה הנ”ל סביב .
   פתרון:
   נניח: נבדוק את תנאי המשפט:
   תנאי ראשון: תנאי שני:
   בעלת נגזרות חלקיות רציפות בסביבת הנקודה.
   תנאי שלישי: ולכן מוגדרת באופן יחיד בסביבת הנקודה.
   פולינום טיילור מסדר ראשון: נמצא כי: ולכן: נציב בחזרה: