תרגיל בית 5
| סטודנט א’ | סטודנט ב’ | |
|---|---|---|
| שם | עידו פנג בנטוב | ניר קרל |
| ת”ז | 322869140 | 322437203 |
| דואר אלקטרוני | ido.fang@campus.technion.ac.il | nir.karl@campus.technion.ac.il |
תרגיל 1
סעיף א’
הקוד הכולל של סעיף א’ וסעיף ב’ ב-python:
import numpy as np
import matplotlib.pyplot as plt
def weight(j, point_x):
w = 1
n = len(point_x)
for i in range(n):
if i != j:
w *= (1 / (point_x[j] - point_x[i]))
return w
def helper_polynom(x, point_x):
phi = 1
n = len(point_x)
for i in range(n):
phi *= (x - point_x[i])
return phi
def lagrange(f, n, a, b):
point_x = np.linspace(a, b, n)
point_y = f(point_x)
w = [weight(j, point_x) for j in range(n)]
# Evaluate p at 0.01 intervals
t = 0.01
x = np.linspace(a, b, int((b - a) / t) + 1)
p = np.zeros_like(x)
phi = np.zeros_like(x)
for k in range(len(x)):
for j in range(n):
p[k] += (w[j] * point_y[j]) / (x[k] - point_x[j])
phi[k] = helper_polynom(x[k], point_x)
p[k] = phi[k] * p[k]
return x, p, phi
def f(x):
return np.cos(2 * np.pi * x)
a = -1
b = 1
n = [2, 5, 10, 20]
# n derivative of f
f_n = [
lambda x: -((2 * np.pi) ** 2) * np.cos(2 * np.pi * x),
lambda x: -((2 * np.pi) ** 5) * np.sin(2 * np.pi * x),
lambda x: -((2 * np.pi) ** 10) * np.cos(2 * np.pi * x),
lambda x: ((2 * np.pi) ** 20) * np.cos(2 * np.pi * x)
]
graph_i = plt.figure()
plt.title("Interpolant evaluations")
plt.plot(np.linspace(a, b, 100), f(np.linspace(a, b, 100)))
for k in range(len(n)):
# Interpolant evaluation
plt.figure(graph_i.number)
x, p, phi = lagrange(f, n[k], a, b)
plt.plot(x, p, "--")
# Absolute error
graph_e = plt.figure()
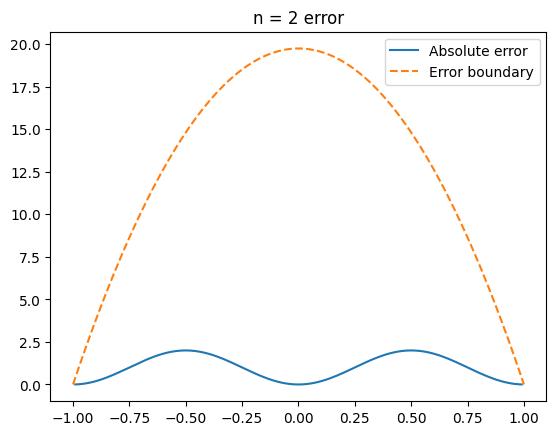
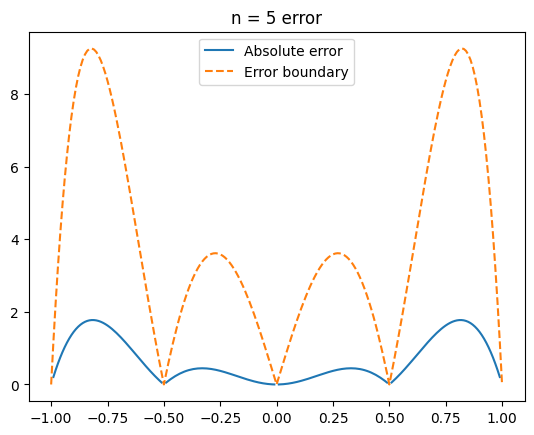
plt.title("n = " + str(n[k]) + " error")
fval = f(x)
e_abs = np.abs(fval - p)
plt.plot(x, e_abs)
# Error boundaries
fnxi = np.max(np.abs(f_n[k](np.arange(-1, 1.25, 0.25))))
e_boundary = np.abs(phi) * (fnxi * (1 / np.math.factorial(n[k])))
plt.plot(x, e_boundary, "--")
plt.legend(["Absolute error", "Error boundary"])
plt.figure(graph_i.number)
plt.legend(["f(x)", "n=2", "n=5", "n=10", "n=20"])
plt.show()
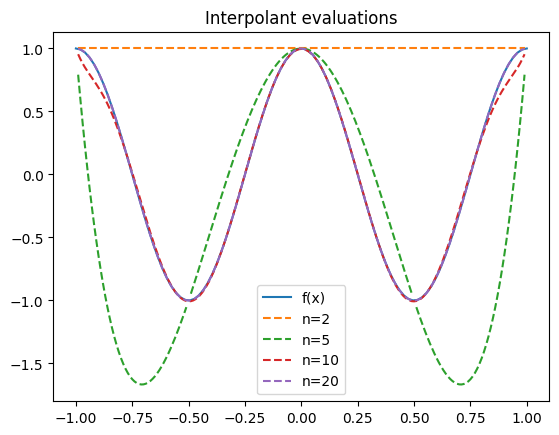
הערה:
הגרפים של
ו- מאוד דומים, ולכן הם פשוט נמצאים בגרף אחד על השני.
סעיף ב’
מאחר והנגזרות של
ולכן מספיק לחשב את ערכי הנגזרת רק בהן. ברור שעבור רוב הנקודות הערכים יהיו זהים, אבל זה רק מוסיף כמה בדיקות בודדות, אז טוב לקחת מקדם ביטחון.
הערה:
ה-
שלנו בשאלה הוא שונה מה- שנתונה בנוסחה (וזה למה הוגדר שונה מ- בשאלה). לכן, בקוד, ה- שאנו משתמשים בו לחישוב הוא , כך שמקבלים את הנוסחה:
קיבלנו כי החסם לשגיאה אכן מהווה חסם לשגיאה האמיתית:
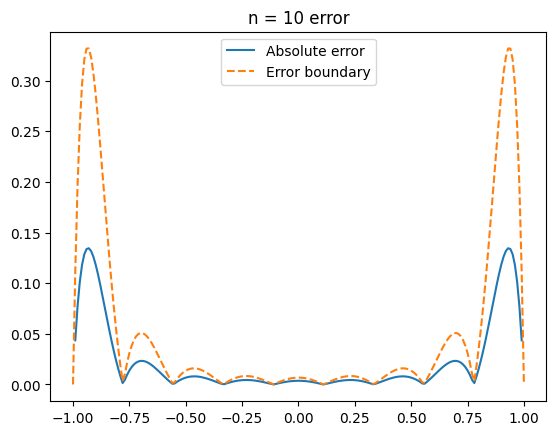
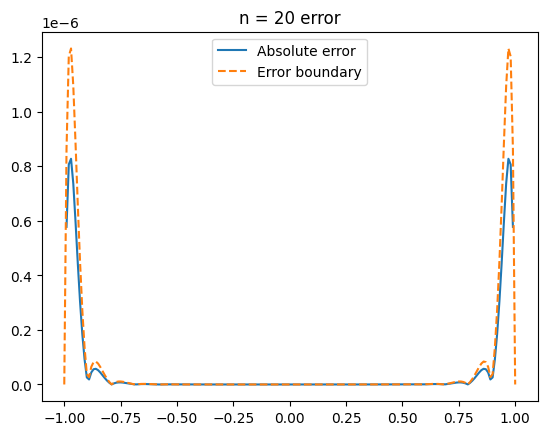
תרגיל 2
סעיף א’
נחשב את פולינום הבסיס עבור כל אחד מה-
סעיף ב’
נשים לב שקיבלנו שהסכום של פולינומי הבסיס קבוע, לכן נשער שלא משנה אילו
נוכיח את ההשערה:
ניקח פונקציה
לפי הגדרה קירוב פולינומי של פולינום הוא הפולינום עצמו, לכן:
מכיוון ש-
כלומר:
בהוכחה שהצגנו למעלה, לא הייתה תלות ב-
סעיף ג’
מכיוון שבכל הגורמים יש לנו
לכן נקבל:
כאשר
מכאן שהמקדם של
תרגיל 3
סעיף א’
לא נוכל להשתמש בשיטת רגרסיה לינארית כדי לפתור ישירות את הבעיה. הסיבה היא שאחד מהתנאים לשימוש בשיטה זו היא שהפונקציה שאליה אנו רוצים להתאים,
אבל כל הפרמטרים
כן נוכל לפתור את הבעיה הזאת בעקיפין עם שיטת הרגרסיה, אם נגדיר פונקציה חדשה,
סעיף ב’
נסמן:
נבנה את המערכת משוואות:
בצורה מטריציונית:
נפתור כעת את הבעיה:
סעיף ג’
נציב את הנתונים במערכת משוואות:
נסיק כי:
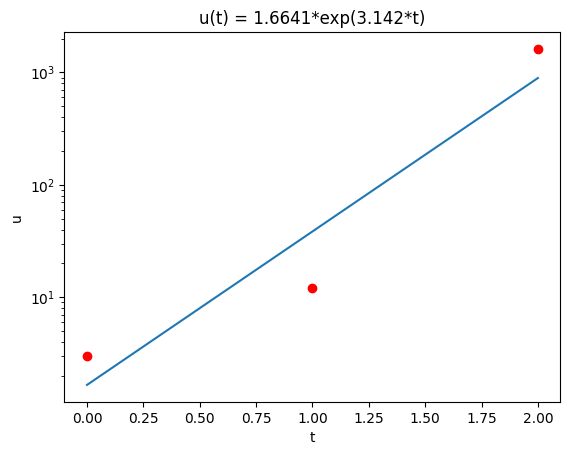
ולכן הפונקציה המקורית היא מהצורה:
הנקודות
קוד python להצגת הגרף והנקודות:
import numpy as np
import matplotlib.pyplot as plt
points_t = [0,1,2]
points_y = [1.1052, 2.4956, 7.3891]
points_u = [np.exp(y) for y in points_y]
plt.plot(points_t, points_u, 'ro')
u = lambda t: 1.6641*np.exp(3.142*t)
ts = np.linspace(0, 2, 100)
plt.plot(ts, [u(t) for t in ts], '-')
plt.title('u(t) = 1.6641*exp(3.142*t)')
plt.yscale('log')
plt.xlabel('t')
plt.ylabel('u')
plt.show()