NUM1_HW004 תרגיל בית 4

תרגיל בית 4

	סטודנט א’	סטודנט ב’
שם	עידו פנג בנטוב	ניר קרל
ת”ז	322869140	322437203
דואר אלקטרוני	ido.fang@campus.technion.ac.il	nir.karl@campus.technion.ac.il

תרגיל 1

סעיף א’

1. נשים לב כי: לכן, לפי משפט ערך הביניים, מאחר ו-, ו- היא פונקציה רציפה, קיימת נקודה כאשר כך ש- .
2. נשים לב כי: לכן, לפי משפט ערך הביניים, מאחר ו-, ו- היא פונקציה רציפה, קיימת נקודה כאשר כך ש- .

סעיף ב’

נקבע את התנאי עצירה לאם:

ואז נדע כי . מאחר ואנחנו לא תמיד נוכל להגיע לפתרון המדויק, אז נקבע תנאי עצירה אחר:

כאשר את נקבע שרירותית. למקרה שלנו, הגדרנו .

clear
clc
close all
 
f = @(x) tanh(x)+0.1*x^2-1;
ans_1 = fzero(f,[0,5]);
eps = 1e-9;
 
%[0,5]
a = 0;
b = 5;
p = 0;
k = 1;
 
abdiff_init = abs(a-b);
 
 
while abs(f(p)) > eps
	[a,b,p] = bisect(f,a,b);
	e = abs(ans_1-p);
	error_1(1,k) = e;
	limit_1(1,k) = abdiff_init/(2^k);
	k = k + 1;
end

axes("XScale", "linear", "YScale", "log");
xlabel("Iterations");
ylabel("Absolute error");
hold on
plot(1:k-1, error_1, "-");
plot(1:k-1, limit_1, "-");
legend("Error", "|b-a|/2^k");
 
%[-5,0]
a = -5;
b = 0;
p = 0;
k = 1;
 
while abs(f(p)) > eps
	[a,b,p] = bisect(f,a,b);
	k = k + 1;
end
 
function [a,b,p] = bisect(f,a,b)
   p = (a+b)/2;
   if f(a)*f(p) < 0
	   b = p;
   elseif f(a)*f(p) > 0
	   a = p;
   end
end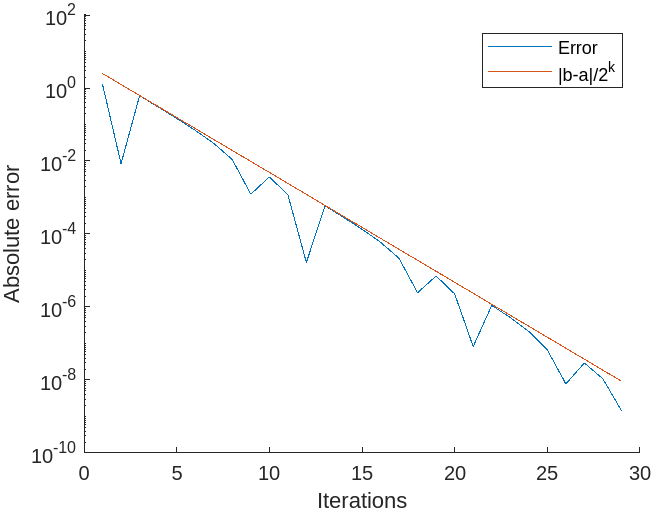

מהגרף אנו רואים שהשגיאה בצעד הראשון חסומה ע”י . כלומר:

אז למשל, עבור התרגיל שלנו:

שזה תואם למה שלמדנו בהרצאה על הלינאריות של התכנסות שיטת החציה.

נוכל להמשיך ולפתח את החסם כדי להסיק כי:

ולכן סדר השגיאה הוא .

סעיף ג’

קיבלנו כי עבור הקטע :
root = 1.2415
ועבור הקטע :
root = -4.4718

תרגיל 2

סעיף א’

סעיף ב’

clear
clc
close all
format long g
 
function x_k = newton(f, f_tag, starting_guess, c, n, epsilon)
	x_k = starting_guess;
	err = [];
	while not(abs(f(x_k, n, c)) < epsilon)
		x_k = x_k - f(x_k, n, c)/f_tag(x_k, n, c);
		err = [err, abs(x_k-sqrt(50.8))];
	end
 
	ord = err(2:end)./err(1:end-1);
 
	axes("XScale", "linear", "YScale", "log");
	xlabel("Iterations");
	ylabel("Absolute error");
	hold on;
	plot(1:length(err), err);
	plot(1:length(ord), ord);
	hold off;
end

סעיף ג’

נבצע איטרציות:

לשם השוואה הפתרון האמיתי הוא .

סעיף ד’

c = 50.8;
n = 2;
epsilon = 1e-14;
 
func = @(x, n, c) x^n-c;
func_tag = @(x, n, c) n*x^(n-1);
 
disp("newton: " + newton(func, func_tag, 10, c, n, epsilon))
 
 

בחרתי כתנאי עצירה, מכיוון שזהו דיוק טוב מספיק עבור הרוב המוחלט של השימושים ההנדסיים.

סעיף ה’

disp("secant: " + secant(func, 10, c, n, epsilon))
 
function x_k = secant(f, starting_guess, c, n, epsilon)
	x_k_prev = 0;
	x_k = starting_guess;
	alpha = [];
	while not(abs(f(x_k,n,c)) < epsilon)
		x_k_next = x_k - f(x_k,n,c)*(x_k-x_k_prev)/(f(x_k,n,c)-f(x_k_prev,n,c));
		x_k_prev = x_k;
		x_k = x_k_next;
		alpha = [alpha, log(abs(x_k-sqrt(50.8)))/log(abs(x_k_prev-sqrt(50.8)))];
	end
	disp("alpha: " + alpha)
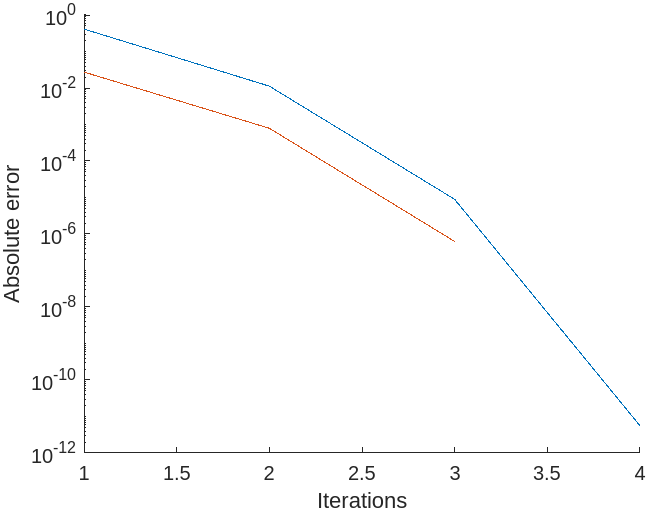
end

אם נחשב נומרית את היחסים בין השגיאות בעזרת הנוסחה הבאה (כפי שמוצג בקוד):

, נקבל כי:

קיבלנו כי מתכנס לערך הקרוב ל-. זוהי תוצאה שתואמת לספרות - סדר השגיאה של שיטת secant היא אכן יחס הזהב.

תרגיל 3

ניחוש התחלתי .

סעיף א’

נרשום את המערכת משוואות:

סעיף ב’

clc
clear
close all
format long g
 
x_init = [1;1;1];
real_ans = fsolve(@f, x_init);
n = 7;
 
[x,k,e] = newtons(@f, @J, x_init, n, real_ans);
axes("XScale", "linear", "YScale", "log");
xlabel("Iterations");
ylabel("Absolute error")
hold on
plot(1:n, e)
hold off

function f = f(vec)
	x = vec(1);
	y = vec(2);
	z = vec(3);
	f = [x*y-z^2-2; x*y*z-x^2+y^2-4; exp(x)-exp(y)+z-6;];
end
 
function J = J(vec)
	x = vec(1);
	y = vec(2);
	z = vec(3);
	J = [y, x, -2*z; y*z-2*x, x*z+2*y, x*y; exp(x), -exp(y), 1];
end
 
function [x,k,e] = newtons(f, J,x,n, real_ans)
	for k=1:n
		fx = feval(f, x); 
		Jx = feval(J, x);
		p = -Jx \ fx;
		x = x + p;
		e(k) = norm(real_ans-x, 2);
	end
	k = n;
end

סעיף ג’

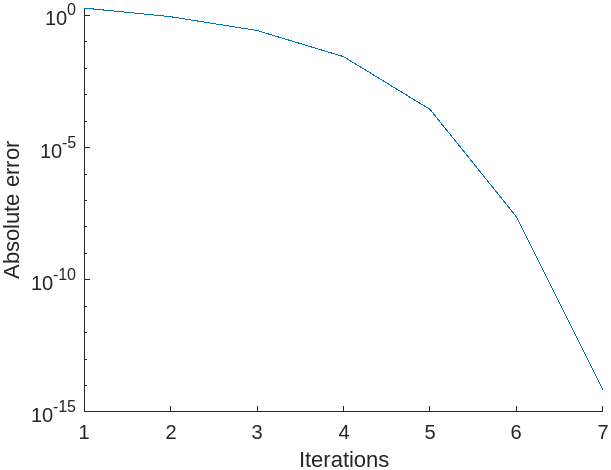
אם נחשב נומרית את היחסים בין השגיאות בעזרת הנוסחה הבאה:

, נקבל כי:

for i = 2:n
	alpha(i-1) = log(e(i))/log(e(i-1));
end
 
>> alpha

קיבלנו כי מתכנס לערך הקרוב ל-. זוהי תוצאה שתואמת לכך שסדר השגיאה של שיטת ניוטון היא , גם עבור מערכת משוואות לא לינאריות.