NUM1_HW003 תרגיל בית 3

תרגיל בית 3

	סטודנט א’	סטודנט ב’
שם	עידו פנג בנטוב	ניר קרל
ת”ז	322869140	322437203
דואר אלקטרוני	ido.fang@campus.technion.ac.il	nir.karl@campus.technion.ac.il

תרגיל 1

סעיף א’

נניח כי האיטרציות מתכנסות לפתרון , כלומר ש- .
נציב בשיטה:

היות ו- הוא פתרון של המערכת, הוא מקיים , ולכן:

סעיף ב’

נציב :

זוהי הצורה המטריציונית של שיטת יעקובי.

סעיף ג’

כתיב אינדקסי לצורה המטריציונית האחרונה שקיבלנו, רק הפעם לא נציב :

סעיף ד’

נרשום את השיטה האיטרטיבית בצורה מטריציונית כך שנקבל משוואה מהצורה:

נשים לב שהיא כבר נתונה לנו בהתחלה בצורה זו ולכן:

תנאי מספיק והכרחי להתכנסות הוא שהרדיוס הספקטרלי של יקיים:

נמצא ע”ע של :

נתון ש- ו- הם ע”ע של , ולכן:

נשווה מקדמים בין שתי המשוואות שקיבלנו:

קיבלנו שהע”ע העצמיים, של תלויים ב-:

הרדיוס הספקטרלי של הוא המקסימלי ביניהם, ולכן:

כאשר בשוויון השלישי לקחנו בחשבון את הנתון ש- חיוביים וממשיים.
נדרוש ש-, אז נפרק למקרים:

או:

לסיכום:

סעיף ה’

קצב ההתכנסות נתון ע”י:

כלומר, נצטרך למצוא מתי הביטוי ב- הוא הכי קטן.
כדי לקבל שהביטוי יהיה כמה שיותר קטן, נדרוש שהביטויים בתוך ה- יהיו שווים. אחרת, פשוט יבחר את הגדול מביניהם.

לכן קצב ההתכנסות יהיה:

תרגיל 2

סעיף א’

סעיף ב’

סעיף ג’

close all
clear;
clc;
 
A = [1, 0, 0, 0, 0, 1/sqrt(2);
	0, 0, 0, 1, 0, 1/sqrt(2);
	0, 1, 0, 0, 1, 0;
	0, 0, 1, -1, 0, 0;
	0, 0, 0, 0, 1, 1/sqrt(2);
	0, 0, 0, 0, 0, 1/sqrt(2)];
x_ans = [1;-1;1;1;1;-sqrt(2)];
b = [0;0;0;0;0;-1];
 
A_T = A';
 
A_tilde = A_T*A;
b_tilde = A_T*b;
 

 
k = 50;
 
 
x_jacobi = zeros(length(x_ans),1);
for i = 1:k
	prev_x = x_jacobi(:);
	x_jacobi = jacobi(A_tilde, b_tilde, x_jacobi);
	r_j(i) = norm(A_tilde*x_jacobi-b_tilde, inf);
	d_j(i) = norm(x_jacobi - prev_x, inf);
	e_j(i) = norm(x_jacobi - x_ans, inf);
end
 
figure()
axes('XScale', 'linear', 'YScale', 'log')
hold on;
plot(1:k, r_j, "-");
plot(1:k, d_j, "-");
plot(1:k, e_j, "-");
 
x_gz = zeros(length(x_ans),1);
for i = 1:k
	prev_x = x_gz(:);
	x_gz = gz(A_tilde, b_tilde, x_gz);
	r_gz(i) = norm(A_tilde*x_gz-b_tilde, inf);
	d_gz(i) = norm(x_gz - prev_x, inf);
	e_gz(i) = norm(x_gz - x_ans, inf);
end
 
 
plot(1:k, r_gz, "-");
plot(1:k, d_gz, "-");
plot(1:k, e_gz, "-");
 
legend("r Jacobi", "d Jacobi", "e Jacobi", "r GZ", "d GZ", "e GZ");
hold off;

function x_k_1 = jacobi(A, b, x_k)
	x_k_1 = x_k;
	for i = 1 : length(x_k)
		sum = 0;
		for j = 1:length(x_k)
			if j ~= i
			 sum = sum + A(i,j)*x_k(j);
			end
		end
		x_k_1(i) = (1/A(i,i))*(b(i)-sum);
	end
end
 
function x_k_1 = gz(A, b, x_k)
	x_k_1 = x_k;
	for i = 1 : length(x_k)
		sum = 0;
		for j = 1:i-1
			sum = sum + A(i,j)*x_k_1(j);
		end
		for j = i:length(x_k)
			sum = sum + A(i,j)*x_k(j);
		end
		x_k_1(i) = x_k(i) + (1/A(i,i))*(b(i)-sum);
	end
end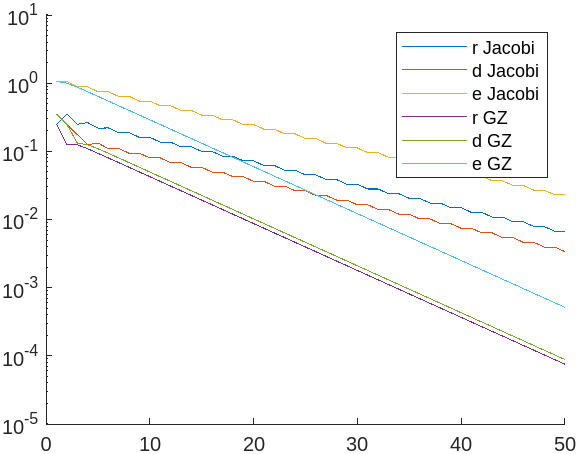

לפי הגרף ניתן לראות ש- ו- מתכנסים יחד עם , ניתן לראות שבהתחלה השגיאה גדולה בהרבה מהנורמות האחרות, אך ככל שהאיטרציות מתקדמות הנורמות של נותנות קירוב יותר טוב של השגיאה.

כלומר בכמות איטרציות נמוכה הנורמות של , אינן מתארות טוב את הנורמה של בצורה טובה. בכמות איטרציות גבוהה, הם מתארים את יחסית טוב.

סעיף ד’

G = eye(length(A_tilde)) - diag(diag(A_tilde))\A_tilde;

נחשב נורמה של ב-matlab:

>> norm(G, inf)
ans =
	1.0607

ולכן:

כאשר השיטה מתכנסת, במקרה שלנו מכיוון שהנורמה גדולה מ-1 לא ניתן לדעת.

סעיף ה’

נחשב את הע”ע של ב-matlab:

>> eig(G)
ans =
   -0.9239
   -0.3827
	0.3827
	0.9239
	0.7071
   -0.7071

ולכן, מאחר ו-, אז:

ניתן לומר ששיטת יעקובי מתכנסת כי הוא תנאי הכרחי ומספיק להתכנסות.

סעיף ו’

[a ,eig_G] = eig(G);
values = diag(eig_G);
max_val_abs = max(abs(values));
 
figure()
axes('XScale', 'linear', 'YScale', 'log')
hold on;
rho_G_vec = arrayfun(@(n) max_val_abs^n, 1:k);
plot(1:k, rho_G_vec, "-");
plot(1:k, e_j, "-");
legend("rho G", "norm e");
hold off;

function x_k_1 = SOR(A, b, x_k, w)
	x_k_1 = x_k;
	for i = 1 : length(x_k)
		sum = 0;
		for j = 1:i-1
			sum = sum + A(i,j)*x_k_1(j);
		end
		for j = i:length(x_k)
			sum = sum + A(i,j)*x_k(j);
		end
		x_k_1(i) = x_k(i) + (w/A(i,i))*(b(i)-sum);
	end
end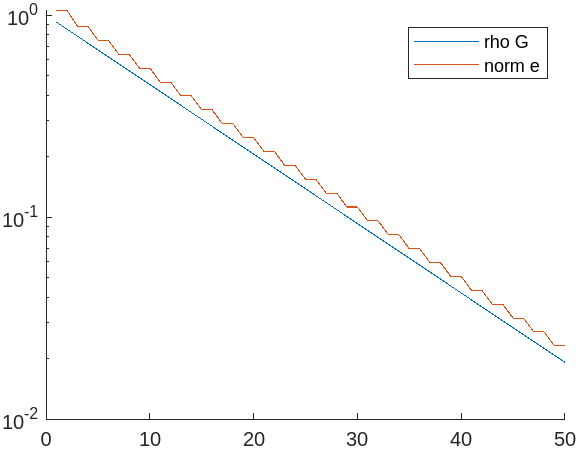

מהגרף ניתן לראות ש- הוא קירוב מאוד טוב של השגיאה שלנו.

סעיף ז’

figure();
axes('XScale', 'linear', 'YScale', 'log')
hold on;
for w = 0.75:0.25:1.75
	x_SOR = zeros(length(x_ans),1);
	e_SOR = zeros(k, 1);
	for i = 1:k
		x_SOR = SOR(A_tilde, b_tilde, x_SOR, w);
		e_SOR(i) = norm(x_SOR - x_ans, inf);
	end
	semilogy(1:k, e_SOR, "-");
end
legend('w = 0.75', 'w = 1.00', 'w = 1.25', 'w = 1.50', 'w = 1.75')
hold off;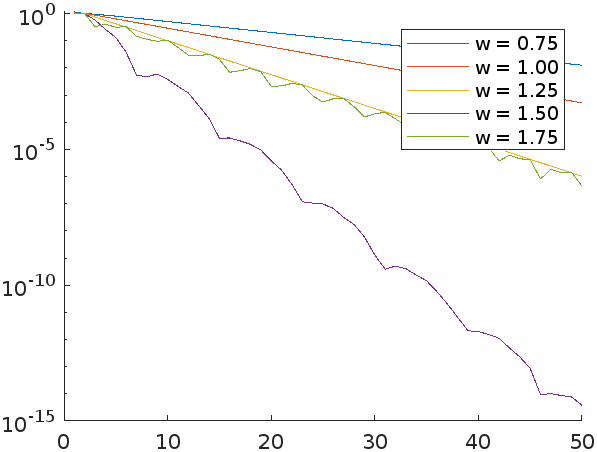

מהגרף ניתן לראות שהשיטה מתכנסת הכי מהר עבור .