NUM1_HW001 תרגיל בית 1

תרגיל בית 1

	סטודנט א’	סטודנט ב’
שם	עידו פנג בנטוב	ניר קרל
ת”ז	322869140	322437203
דואר אלקטרוני	ido.fang@campus.technion.ac.il	nir.karl@campus.technion.ac.il

תרגיל 1

נדרג עד שנקבל מטריצה משולשת עליונה:

נפתור עבור :

ועבור שאר ה--ים:

אכן הגענו לתשובה:

תרגיל 2

סעיף א’

סעיף ב’

את פעולות השורה ניתן לייצג בעזרת כפל מטריצות מצד שמאל עם המטריצות הבאות:

פעולה ראשונה:

פעולה שנייה:

פעולה שלישית:

סעיף ג’

סעיף ד’

על מנת למצוא את מתוך המטריצות של פעולות השורה שמצאנו בסעיפים קודמים, נחבר את המטריצות ההופכיות להן שמצאנו בסעיף הקודם.

מחיבור מטריצות אלו קיבלנו מטריצה משולשית תחתונה, וכעת נראה שהכפלתה במטריצה המשולשית העליונה שקיבלנו במהלך הדירוג בשיטת גאוס נותן לנו את המטריצה המקורית.

סעיף ה’

פירוק המטריצה לפי הסעיפים הקודמים:

פירוק המטריצה לפי תרגול 2 שאלה 4:

קיבלנו שהפירוקים שונים, הדבר קורה כי השתמשנו באלגוריתמים שונים. פעם אחת השתמשנו באלגוריתם דוליטל, ופעם שניה ב-”crout”.

תרגיל 3

סעיף א’

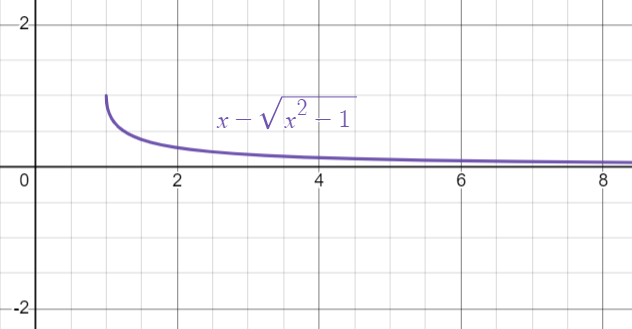
הראו כי:

פתרון:

סעיף ב’

איזה מצורות אלו טובה יותר לחישוב נומרי? נמקו למה, והציגו דוגמה הממחישה זאת.
פתרון:
אנו נעדיף את הביטוי הימני לחישוב נומרי. בביטוי השמאלי ישנו חיסור, שגורם ליותר טעויות כאשר מחסרים שני מספרים מאוד קרובים אחד לשני. למשל, עבור , עם דיוק של 3 ספרות, ביטוי שמאל יניב לנו:

ואלו ביטוי ימין:

סעיף ג’

עבור אלו ערכים של ההבדל משמעותי?
פתרון:
ככל ש- גדול יותר, ההבדל נעשה יותר ויותר משמעותי, כי הביטוי שואף יותר ויותר לאפס, מה שיגרום לחישוב הנומרי להגיע למסקנה הלא נכונה שאין תשובה.

תרגיל 4

בשאלה זו נחקור איבוד דיוק במחשב. נתחיל עם הסדרה:

שימו לב שהערך האנליטי המדויק הוא:

סעיף א’

בצעו את האיטרציות במחשב (לפחות עד ) ושרטטו את השגיאה האבסולוטית כתלות ב-.

פתרון:

a = zeros(1,30);
a(1) = 1/3;
err_abs = zeros(1,30);
 
for n = 1:29
	a(n+1)=10*a(n)-3;
	err_abs(n+1) = abs(a(n+1)-1/3);
end
 
figure;
plot(1:30, err_abs, LineWidth=3)
figure;
semilogy(1:30, err_abs, LineWidth=3)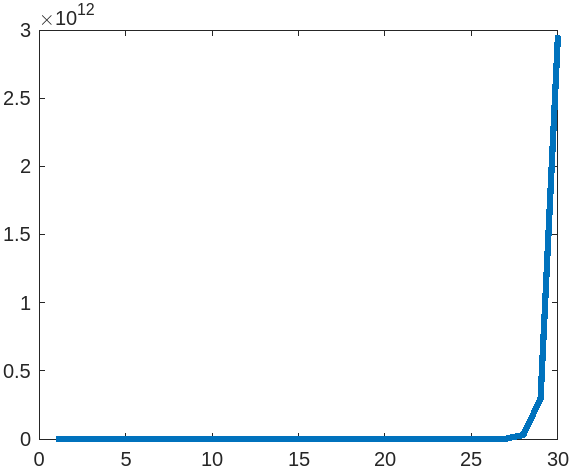

סעיף ב’

איזו פונקציה מתארת את השגיאה כתלות ב-? (מומלץ לצייר את השגיאה כתלות ב- על סקאלה לוגריתמית בציר ).
פתרון:

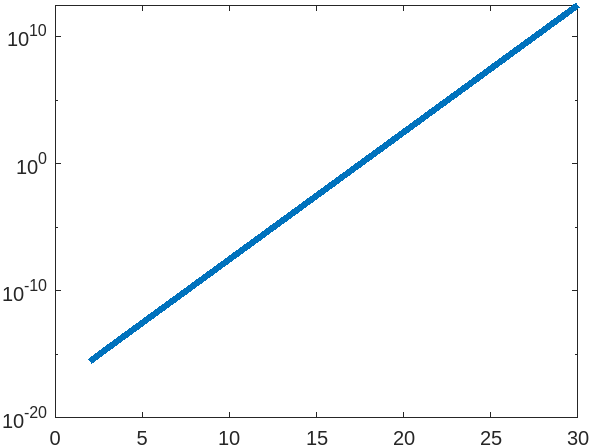
קיבלנו קו ישר בסקאלה לוגריתמית, מה שמעיד שהפונקציה אקספוננציאלית.

סעיף ג’

כדי להסביר מדוע השגיאה כל פעם גדלה, ואף גדלה כל פעם פי , נניח כי אנחנו מחשבים עד דיוק של ספרות, כך שכבר בהתחלה יש לנו איזושהי שגיאה :

כל פעם אנו מגדילים את השגיאה פי , ולכן בגרף הלוגריתמי על בסיס אנחנו מקבלים קו ישר.

שאלה 5

סעיף א’

ניקח מטריצה משולשית עליונה בגודל .
נפתח את הדטרמיננטה לפי העמודה הראשונה:
מכיוון שכל האיברים בעמודה הראשונה שאינם האיבר הראשון הם אפס, נקבל שתוצאת הדטרמיננטה היא האיבר הראשון כפול המינור שלו.
לכן קיבלנו שהמינור שלו הוא: שגם הוא מטריצה משולשית עליונה.
נעשה גם לו פיתוח דטרמיננטה לפי העמודה הראשונה ומאותן סיבות כמו בפעם הראשונה נקבל את הערך שבשורה הראשונה, בעמודה הראשונה כפול המינור שלו.
נעשה את אותה הפעולה באופן רקורסיבי עד שנגיע למינור בגודל 1, שהדטרמיננטה שלו היא הערך עצמו. ונקבל שהדטרמיננטה של המטריצה היא מכפלת כל הערכים שעל האלכסון הראשי.
באופן דומה אפשר לפתח את הדטרמיננטה של מטריצה משולשית תחתונה לפי העמודה האחרונה ולקבל את אותה המסקנה.

סעיף ב’

מכיוון שהוכחנו בסיף א. שהדטרמיננטה של מטריצה משולשית (עליונה \ תחתונה) היא מכפלת איברי האלכסון, נציב את זה לתוך הזהות הנתונה ונקבל:

ולכן אם הדטרמיננטה של :$$
\det(A)=\det(LU)=\prod_{}^{}l_{ii}\prod_{}^{}u_{ii}