NUM1_010 גזירה נומרית

מבוא

למרות שאנו מכירים דרכים אנליטיות לחישוב נגזרות מחדו”א 1, ישנם סיבות לחשב אותן נומרית. אחת הסיבות היא אם אנו לא יודעים בוודאות מהו ה- שאנו רוצים לגזור, או ש- עצמה היא מסובכת מדי לגזירה אנליטית. אז למשל, גזירה נומרית היא פעולה מאוד נפוצה בחישוב משוואות דיפרנציאליות. כדי לקבל נוסחאות עבור גזירה נומרית, ניעזר בקירוב פולינומי של .

פיתוח שיטות בעזרת טור טיילור

מחדו”א 1, הנגזרת של פונקציה בנקודה נתונה ע”י:

הגדרה זו משתמשת בערכים של ליד נקודת הגזירה . אז כדי לקבל נוסחה לחישוב הנגזרת, אנו לרוב נבחר נקודות במרחקים שווים ליד הנקודה, ונבנה קירוב של מנקודות אילו.

בהנחה ו- חלקה מספיק, ככל ש- קטן, השגיאה שלנו תקטן.

שיטות בשתי נקודות

כאשר נפתח את לטור טיילור סביב , נוכל לפתח שיטות הפרשים לפנים ולאחור. למשל, בנוסחת הפרשים לאחור, נבחר ונפתח לטיילור:

נסדר ונקבל:

בשיטה לפנים אנו נבחר ונקבל:

כאשר
נוכל להשתמש בשיטה לפנים פעמיים כדי לקבל את הנגזרת השנייה:

כאשר .

שיטה בשלוש נקודות

שיטת ההפרשים המרכזיים עבור ניתנת כאשר נפתח סביב גם ב- וגם ב-, כך שנקבל:

נחסר בין שתי המשוואות, ונקבל:

כאשר .
באותו אופן נוכל לקבל את הנגזרת השנייה מתוך שלוש נקודות:

נחסר בין שני המשוואות ונקבל את שיטת ההפרשים המרכזיים לנגזרת שנייה:

כאשר .

דוגמה:

הטבלה הבאה מציגה את השגיאה עבור הגזירה הנומרית () של הפונקציה בנקודה , עם מרווחים , בעזרת שיטות עם שתי נקודות, שלוש נקודות, וחמש נקודות (שלא למדנו ולא באמת צריך לדעת).

השגיאה של גזירה נומרית. משמאל לימין, מהעמודה השנייה, שגיאה בשני נקודות, שגיאה בשלוש נקודות, ושגיאה בחמש נקודות. הגרף מוצג בסקאלת log-log.

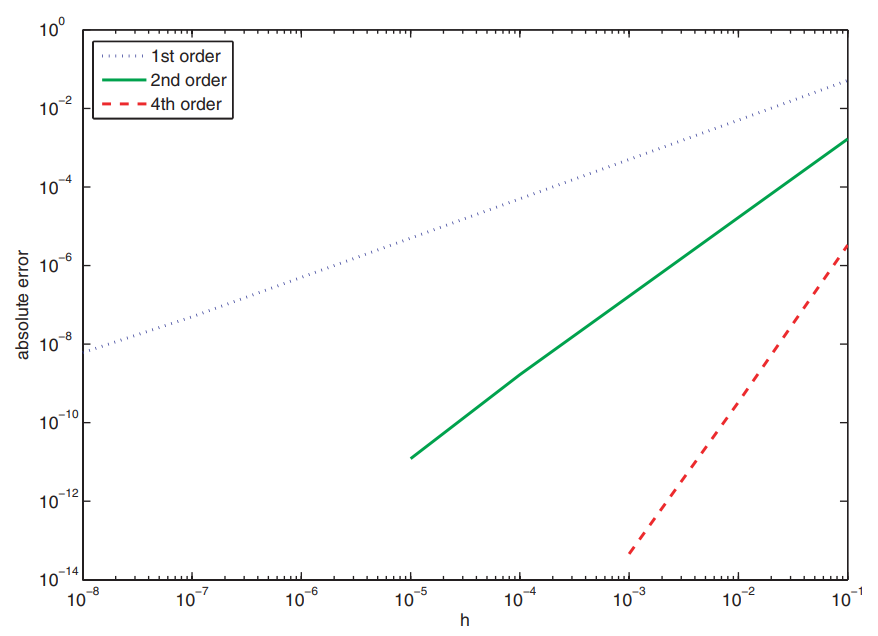
נוכל גם להציג את התוצאות על גרף:

שגיאה אמיתית של שלושת השיטות. שימו לב ששיפוע הגרף מציג לנו את סדר השגיאה ().

אקסטרפולציית ריצ’רדסון

בדומה לאינטגרציית רומברג, נוכל לבצע את אקסטרפולציית ריצ’רדסון על שיטות נומריות לחישוב נגזרות כדי לקבל סדר שגיאה יותר גבוה.

נחשב את הנגזרת השנייה של ב-, פעם בעזרת ופעם בעזרת :

נכפיל את הנוסחה הראשונה ב-, נחסר את השנייה, ונחלק ב-, כדי לקבל שיטה לחישוב נגזרת שנייה עם שגיאה מסדר :

נרשום בצורה הדומה לשיטות הקודמות:

כאשר .