הערה:
לצערי אני נאלץ לרשום גם את השאלות עצמן במבחן הזה כי סגל הקורס כותב ומצייר כמו יד שמאל של סבתא שלי.
שאלה 1
פח שעשוי מאלומיניום
תיאור התהליך
- חומר הגלם הוא חוט בעל חתך עגול בקוטר
המיוצר במשיכה. - כיוון הערגול הוא במקביל לציר של החוט.
- חתך הפס בסיום הערגול הוא בקרוב מלבן, בעובי
ורוחב .
נתון גם כי:
סעיף א’
מהו הקוטר של חומר הגלם,
פתרון:
בכניסה, הנפח של חומר הגלם באורך
ביציאה, הנפח של המוצר באורך
משימור נפח, בהנחה ואין שינוי באורך, מתקיים
נציב נתונים ונקבל:
סעיף ב’
באיור הבא גרף
פילוג המאמצים עבור שתי מערגלות שונים
הסבר ונמק:
- מדוע קטן המאמץ
- מדוע התרחקה הנקודה בה נקבל את המאמץ המקסימלי מהכניסה למערגלת.
פתרון:
-
מ[[MNF1_003 Bulk Deformation Processes#Rolling#Roll Pressure Distribution|פילוג מאמצים בערגול]] (במקרה שלנו,
): ניתן לראות שכאשר מקטינים את
, המקסימום של קטן - כלומר, המאמץ המקסימלי קטן. -
כאשר
קטן, יותר קשה לכוח המניע את החומר לקדם אותו דרך המערגלת. כלומר, נדרש יותר כוח כדי להאיץ את מהירות החומר גלם למהירות המערגלת. בהנחה וכוח זה נשאר קבוע (כלומר, ההספק קבוע), כאשר נקטין את , ייקח יותר דרך כדי להאיץ את החומר גלם למהירות המערגלת. לפיכך, הנקודה בה המאמץ מקסימלי תנוע ימינה.
סעיף ג’
מהו מקדם החיכוך המינימלי שיאפשר את תהליך הערגול?
פתרון:
דג”ח על הכניסה למערגל, ב-
. המאמץ נובע מהחיכוך, שתמיד מקיים כאשר יש תנועה. במקרה הדיפרנציאלי, מוחלף במאמץ .
נדרוש שתהיה תאוצה בכיוון
נצמצם ונקבל:
נציב
סעיף ד’
לפי [[MNF1_003 Bulk Deformation Processes#Rolling#Roll Torque and Power|הספק של ערגול]]:
אנו גם יודעים שב[[MNF1_003 Bulk Deformation Processes#Rolling#Roll Pressure Distribution|ערגול]]:
ולכן:
נציב נתונים ונקבל:
הערה:
לא יודע אם זה התשובה הנכונה, כי סגל הקורס מאוד נחמד וממש מפרסם פתרונות למבחני עבר.
סעיף ה’
מצא את מיקום הנקודה הניטרלית
- מהירות היציאה הקווית של הפח היא
. - אין שינוי ברוחב הפח לאורך המערגלת.
פתרון:
אין לי שמץ, אין לזה נוסחה (יש בספר, לא למדנו אותה). אפשר אולי להניח שמהירות היציאה הקווית היא
סעיף ו’
על מנת להקטין את השקיעה הרדיאלית של המערגלת במרכזה, הוסיפו זוג מערגלות ברדיוס
פתרון:
אין לי שמץ. תודה רבה לסגל הקורס שיודע איזה חומר הוא כן העביר ואיזה חומר הוא לא העביר לסטודנטים.
שאלה 2
כבישת אטם - נתון אטם מעופרת (lead gasket - חפשו בגוגל) בצורת מלבן וחתך מלבני. בתחילת התהליך המידות החוסמות של האטם הן אורך של
האטם נכבש בכוח
סכימת האטם וחתך בה רואים גם את הכבישה.
נתונים:
בנוסף, הקשיית המעוותים זניחה, ויש להניח קריטריון כניעה פון מיזס.
סעיף א’
שרטט בצורה איכותית את החתך של האטם בגובה
פתרון:
מאחר ומתקיים שימור נפח, נסיק כי החתך
החתך
לפני ואחרי הכבישה.
סעיף ב’
צייר דיאגרמת גוף חופשי לאלמנט בחומר הנכבש (רוחב
פתרון:
לפי [[MNF1_003 Bulk Deformation Processes#Forging#Slab Method of Analysis|שיטת הטבלה]]:
דג”ח על אלמנט ברוחב
וגובה .
אנו מניחים כי:
- הבעיה סימטרית ביחס לציר ה-
. - ישנו חיכוך קינטי
, כאשר במקרה שלנו, הוא המאמץ בכיוון האופקי במגע עם הקיר, ו- הוא הלחץ הנורמלי, . - מצב עיבורים מישורי (
).
סעיף ג’
תארו באופן סכמתי את פילוג המאמצים על המקב במהלך הכבישה (התייחסו לחתך האטם
פתרון:
מ[[MNF1_003 Bulk Deformation Processes#Forging#Slab Method of Analysis|פילוג לחץ בכבישה]]:
כאשר
צורת פילוג מאמצים זה הוא:
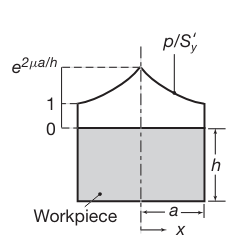
פילוג המאמצים בחתך, באופן מנורמל
.
סעיף ד’
מצא את כוח המקב
פתרון:
הכוח הוא פשוט סכימה של הלחץ לאורך כל שטח החתך (החתך שנמצא במישור
כאשר את
שאלה 3
בשרטוט מתואר חלק שהתקבל ביציקה לפני תהליך כרסום.
שרטוט החלק הנתון. נדרש לעבד את חלקו העליון (המדרגה האמצעית).
נתון כי קוטר הכרסום הוא
בניסוי התקבל גרף הכוח השקול כנגד זווית סיבוב הכרסום:
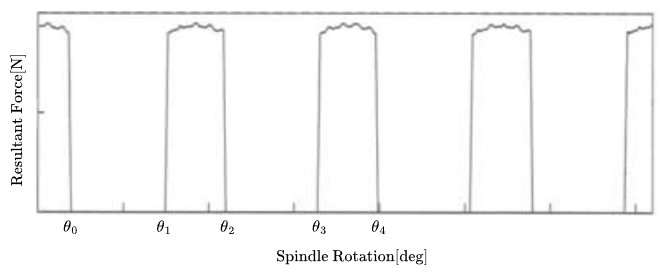
סעיף א’
מהו מספר השיניים המקסימלי בכרסום?
פתרון:
מהגרף ניתן לראות שישנם רגעים בהם הכוח שמפעיל הכרסום הוא אפס. כלומר, ישנם רגעים בהם אין שן על העובד. לפיכך מספר השיניים המקסימלי הוא כך שיאפשר רגעים בהם אין שן על העובד:
תיאור המרווח המינימלי בין שיניים על הכרסום. כל מרווח קטן יותר יעיד על כך שתמיד תהיה שן על העובד.
לפיכך, עלינו לדרוש ש-
לפיכך, מספר השיניים המקסימלי בכרסום הוא
סעיף ב’
מצא את הפרש הזוויות
פתרון:
הפרש הזוויות
סעיף ג’
הנח כי:
מהי הזווית
פתרון:
נציב את פתרון סעיף קודם בהנחות:
עבור ההנחה השנייה:
נשים לב כי
מהגרף ניתן לראות ש-
מהגרף ניתן לראות ש-
נציב ערכים שכבר מצאנו:
ולכן
לסיכום:
הערה:
יש דרך יותר פשוטה להראות את זה, לא היה לי כוח לשרטט על הגרף.
סעיף ד’
מהו מספר השיניים בכרסום (לפי סעיפים ב’ ו-ג’)?
פתרון:
נדמה את רגע
רגע
אנו יודעים שלאחר עוד סיבוב של
שאלה 4
נתון חלק מפלדה מסגסוגת SAE4340 בקשיות
הכרסומת בעלת הספק של
מהירויות הסיבוב האפשריות של הכרסום הן:
מהירויות השולחן האפשריות הן:
יש לעבוד עם קדמה לשן של
ממדי החלק
אופן פעולת הכרסום
הערה:
במבחן רשום ש-
, ופשוט החלפתי ב- כי אחרת זה לא מסתדר מבחינת יחידות.
מה שלא ציפיתי שיקרה, שלפי התשובות שאני רואה ברפרנסים לפעמים, שכנראה סגל הקורס לא יודע להמיר יחידות וחושב ש-, ואז כל התשובות יוצאות פי ממה שאני רושם. אם זה המצב, ואני נופל על זה במבחן, אני אבקש להקפיא את המחקר של האחראי.
אם הם מתכוונים ל-, אז שיכתבו .
סעיף א’
מהי מהירות סיבוב הכלי שתבחר?
פתרון:
מהירות החיתוך המקסימלית עבור הסכין הנתונה היא
נדרוש שהיא תהיה קטנה מהערך המקסימלי:
לכן, מהמהירויות הנתונות, נבחר ב-
סעיף ב’
מהי מהירות השולחן המתאימה?
פתרון:
אנו יודעים כי [[MNF1_004 Machining Processes#Milling#Key Parameters and Equations|מהירות השולחן]] נתונה ע”י:
נציב פרמטרים ואת
כלומר, אם נעבוד עם קדמה לשן קטנה יותר מ-
אם הייתי מקבל את השאלה הזאתי במבחן הייתי שובר את הראש על זה במשך שעה, כי הייתי מצפה שהתשובה תהיה אחת מהאפשרויות (שוב, סגל קורס מטורף, באמת אין כמוכם).
מסתבר יש לשאלה הזאתי גם פתרון רשמי במודל, אבל שם נתון להם גם שמספר השיניים בכרסום נתון לשינוי, שזה בכלל משנה את השאלה ודורש מהם להתחשב גם בהספק המכאני של הכרסום. אבל בשאלה שנתנו לנו שכחו בכלל מהחלק הזה והשאירו נתונים שלא נשתמש בהם.
סעיף ג’
מהו הכוח המקסימאלי הפועל על השן?
פתרון:
גאומטריית הכרסום
מהאיור ניתן לראות ש:
מאחר וישנן
כאשר
סעיף ד’
מהו ההספק הממוצע הדרוש לתהליך, בתנאים שבחרת?
פתרון:
לפי [[MNF1_004 Machining Processes#Milling#Cutting Force and Power|הספק של כרסום]]:
לכן:
סעיף ה’
מהו זמן העיבוד המינימאלי (עגל תשובתך)?
פתרון:
פתרון:
לפי [[MNF1_004 Machining Processes#Milling#Key Parameters and Equations|זמן עבודה]] אנו יודעים כי:
נציב נתונים ונקבל:
סעיף ו’
שרטט גרף המתאר את השתנות כוח השיבוב ההיקפי הכולל כפונקציה של זווית סיבוב (ציין את ערכי הקיצון).
פתרון:
אם נציב ב-Desmos את הפונקציה שנמצאנו עבור
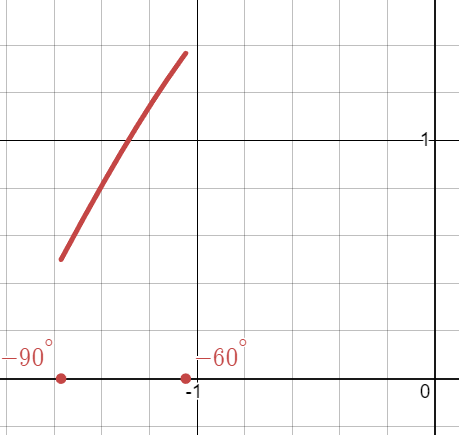
הפונקציה
כאשר