עקרונות יסוד
בפרק זה אנו נעסוק בקבוצה של מנגנונים המעבירים תנועה סיבובית בין שני אלמנטים.
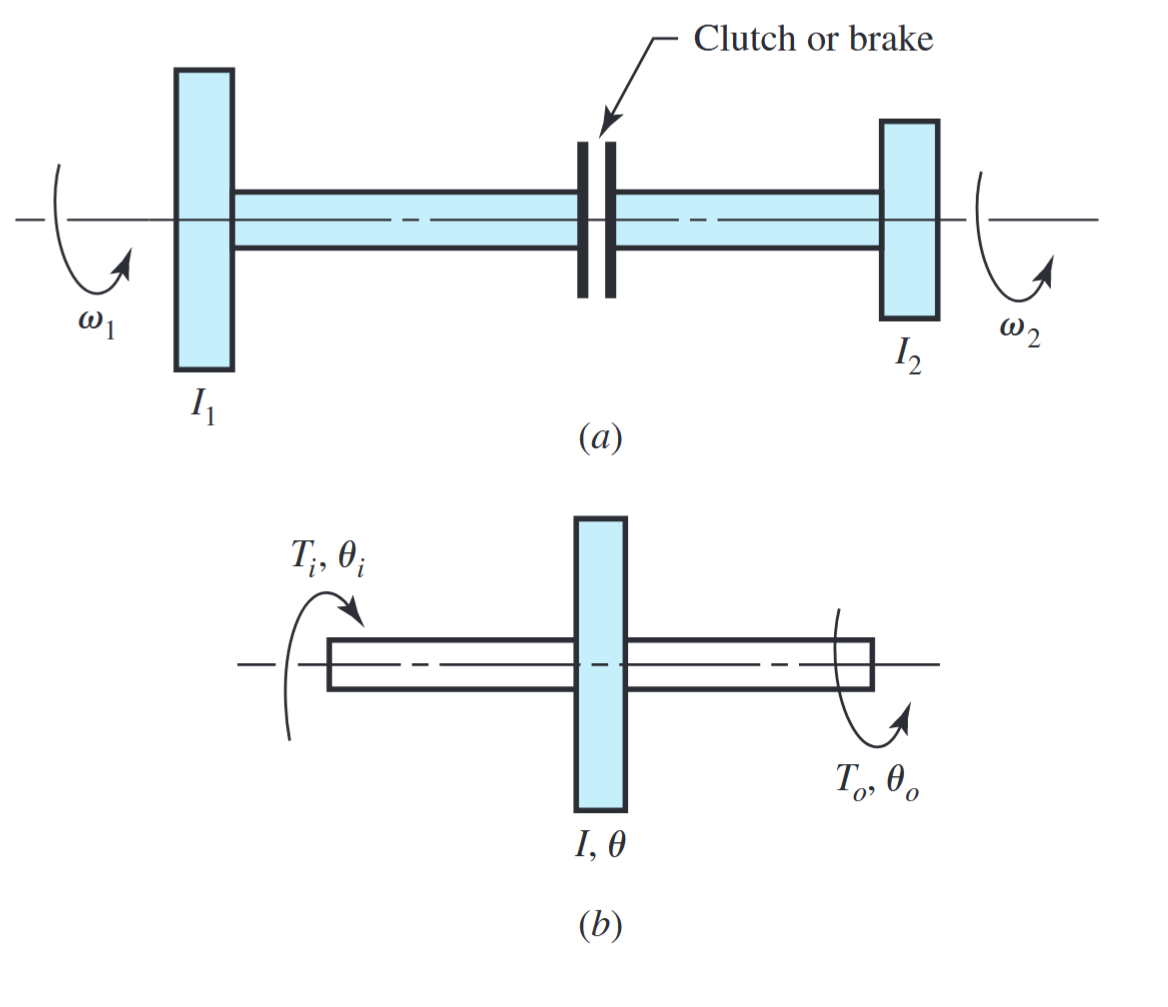
סכמה של (a) מצמד או בלם. (b) גלגל תנופה (flywheel).
בניתוח הביצועים של מצמד או מעצור אנו מעוניינים בגדלים הבאים:
- המומנט המועבר - transmitted torque.
- הכוח המפעיל - actuating force.
- הפסד האנרגיה - energy loss.
- עליית הטמפרטורה - temperature rise.
המומנט המועבר תלוי בכוח המפעיל, במקדם החיכוך ובגיאומטריה של המצמד. זוהי בעיה בסטטיקה שנדרש לפתור לגבי כל גיאומטריה שונה. בקורס אנו עוסקים בממסרות מפחיתות, ולכן המצמד יותקן בד”כ בציר הכניסה לתשלובת שם המומנט נמוך (אך המהירות הזוויתית גבוה).
ניתוח סטטי של מצמדים ובלמים
תהליך הניתוח של מצמד/בלם כללי מתואר כלהלן:
- נניח, נשער, או נמדוד את פילוג לחץ
כלשהו בין משטחי החיכוך. - נמצא את הקשר בין הלחץ הכי גדול והלחץ בכל נקודה.
- נמצא מתוך משוואות הסטטיקה את כוח הבלימה או המומנט, ואת התגובות בריתומים.
כאשר נדרש לתכנן מצמד, בדרך כלל מוגדר המומנט המועבר והמתכנן נדרש לבחור גיאומטריה, את רפידת הבילום ולחשב את הכוח המפעיל.\
ניקח לדוגמה את המקרה של המעצור דלת הבא:
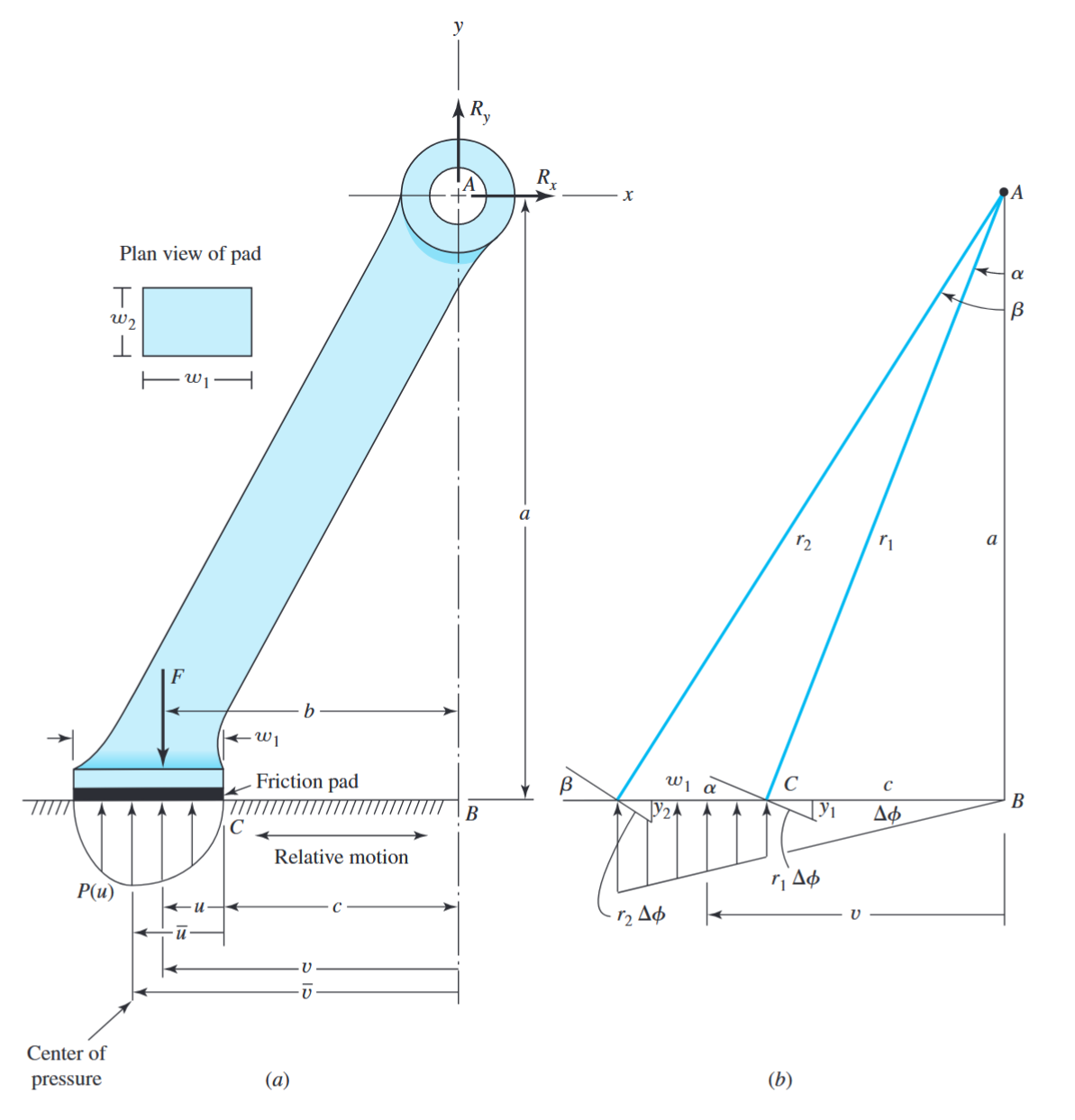
מעצור דלת טיפוסי.
עקב תנועת המשטח התחתון והכוח המפעיל
לכן, קודת מרכז הלחץ של הנעל
נסמן גם את הלחץ הממוצע ב-
נבצע סכום מומנטים סביב הציר, בהנחה וגם הכוח
בהנחה וידוע לנו הלחץ המקסימאלי המותר
ניתן לראות כי הכוח המפעיל
מצמדים ובלמים בעלי תוף פנימי

מצמד פנימי מופעל צנטריפוגלית.