HTF1_HW006 תרגיל בית 6

	סטודנט א’
שם	עידו פנג בנטוב
ת”ז	322869140
דואר אלקטרוני	ido.fang@campus.technion.ac.il

שאלה 1

סכמת הבעיה.

נתונים:

סעיף א’

נמצא את האורך קריטי לזרימה טורבולנטית:

נתיב נתונים ונקבל:

מאחר ואנו לא מגיעים לאזור הטורבולנטי, נוכל להשתמש בפתרון בלסיוס לזרימה למנירית בפלטה שטוחה:

נציב נתונים ונקבל:

סעיף ב’

לפי משוואה :

נציב ערכים ונקבל:

סעיף ג’

לפי משוואה :

ולכן לפי הגדרת מספר נוסלט:

כך שבקצה הלוח, לאחר הצבת ערכים:

לכן שטף החום המקומי, מהגדרת מקדם המעבר חום:

נציב ערכים ונקבל:

סעיף ה’

באותו אופן כמו סעיף קודם, רק הפעם לפי משוואה :

ולכן מקדם מעבר החום הממוצע:

נשים לב שההבדל בין ביטוי זה למקדם מעבר חום לבין מקדם מעבר החום שקיבלנו בסעיף קודם הוא סדר גודל של , ולכן נוכל להסיק ישירות ששטף מעבר החום הממוצע יהיה פי יותר גדול.

שאלה 2

נתונים:

כדי למצוא נתונים על האוויר, נפנה לטבלה A.4 בספר, ונשתמש בטמפרטורה הממוצעת:

נמצא כי:

סעיף א’

נמצא את האורך קריטי לזרימה טורבולנטית:

נתיב נתונים ונקבל:

קיבלנו כי הזרימה המקבילה לצד הארוך של הפלטה תהיה זרימה מעורבת, בעוד הזרימה המקבילה לצד הקצר תהיה רק למינרית.

לפי משוואה :

קצב מעבר החום:

נציב ערכים ונקבל:

סעיף ב’

עבור הצד הקצר הזרימה למינרית, ולכן נוכל להשתמש במשוואה :

לכן קצב מעבר החום:

נציב ערכים ונקבל:

סעיף ג’

כעת האורך קריטי לזרימה טורבולנטית:

כלומר בשני הכיוונים נישאר בזרימה למינרית, והביטוי הבא לקצב מעבר החום תקף עבור הצד הארוך:

והביטוי הבא עבור הצד הקצר:

מאחר ו- , ניתן לראות שנקבל יותר קצב מעבר חום גבוה יותר על הצד הקצר יותר.

שאלה 3

נתונים:

נניח את מקרה הקיצון בו טמפרטורת שפת השבב היא . מאפייני האוויר לפי טבלה A.4 בטמפרטורה ממוצעת הם:

סעיף א’

האורך קריטי לזרימה טורבולנטית:

ולכן הזרימה היא למינרית, ונוכל להשתמש בביטוי הבא (שפותח [[#שאלה 2#סעיף ב’|בשאלה קודמת]]) לחישוב קצב מעבר החום, רק הפעם נתבסס על משוואה בפיתוחה (כך שנקבל קצב מעבר חום מקומי, בקצה הפלטה):

נציב ערכים ונקבל:

זהו קצב מעבר החום המקומי בקצה הפלטה, והוא קצב מעבר החום המינימלי בפלטה, כך שבו הטמפרטורה תהיה הכי גבוהה. אם נדרוש שזה יהיה קצב מעבר החום המקסימלי בכל הפלטה, יתקיים כנדרש.

סעיף ב’

לפי משוואה :

נציב במקום הרלוונטי כמו בפיתוח בסעיף קודם:

נציב ערכים, כאשר נשים לב שבמקרה שלנו, , ש- , ועדיין (כי יש לשים לב למשמעות כל אחד מהגדלים האלו בחישובי הביניים של ):

שאלה 4

סכמת הבעיה. שאלה 7.65 בספר.

נתונים:

סעיף א’

נתחיל מלמצוא את מקדם ההסעה לכדור. לפי משוואה :

אנו מניחים ש- , ולכן:

נציב ערכים ונקבל:

לכן מקדם ההסעה הממוצע הוא:

נבדוק תנאים למודל חום מקובץ:

לכן נוכל להשתמש במודל חום מקובץ. לפי משוואה :

רוצים למצוא את עבורו :

נציב ערכים:

סעיף ב’

נתונים:

לפי משוואה , במקרה הכללי:

במצב מתמיד:

עם הצבת ערכים, נקבל פתרון פיזיקלי יחיד (לא שלילי ולא מדומה):

סעיף ג’

מ[[#שאלה 4#סעיף א’|סעיף א’]]:

לכן, ככל שמהירות הזורם יותר גדולה, מקדם מעבר החום להסעה יותר גדול, ונקבל טמפרטורה יותר גבוה במצב מתמיד:

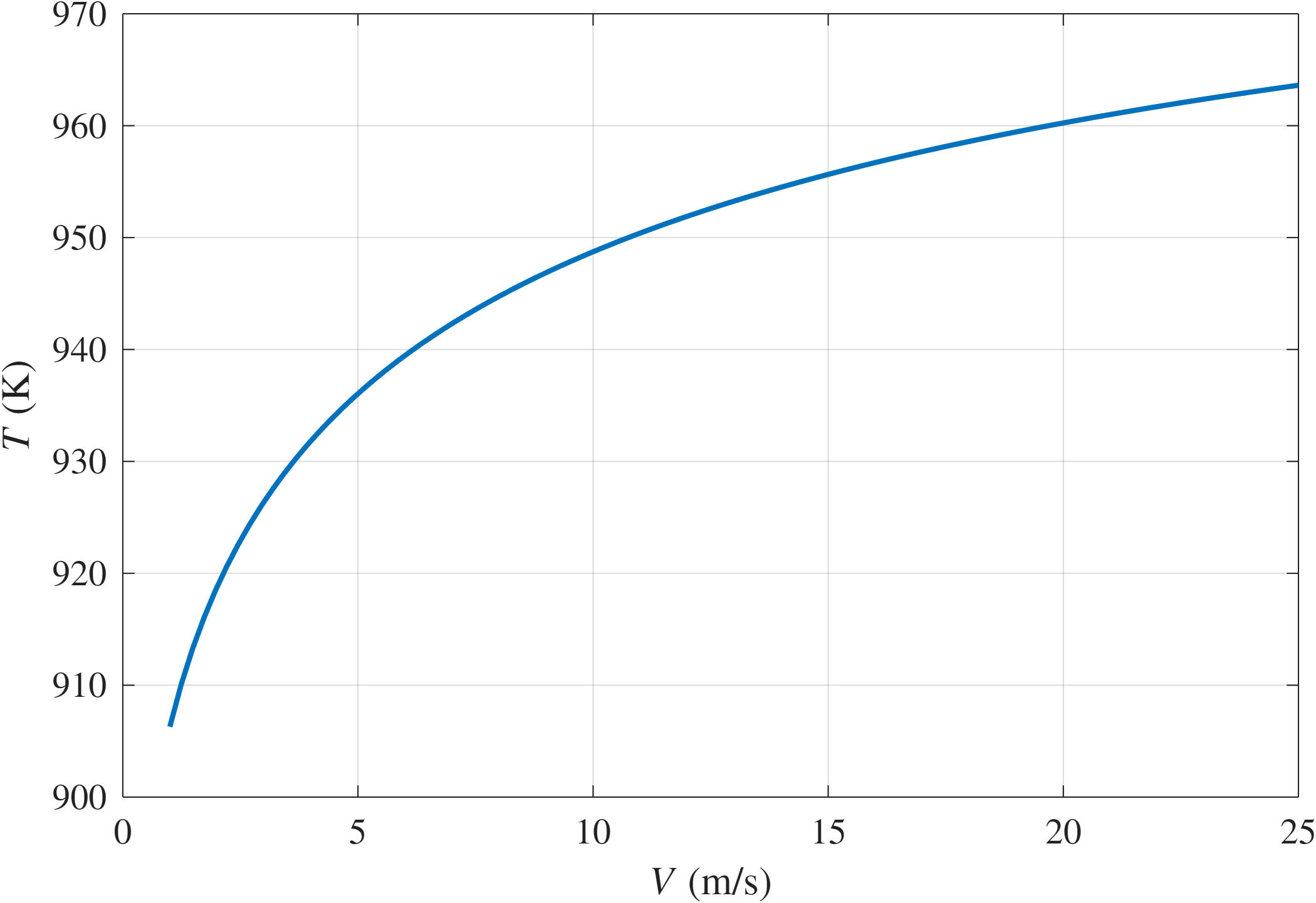
טמפרטורה במצב מתמיד כתלות במהירות הזורם.

סעיף ד’

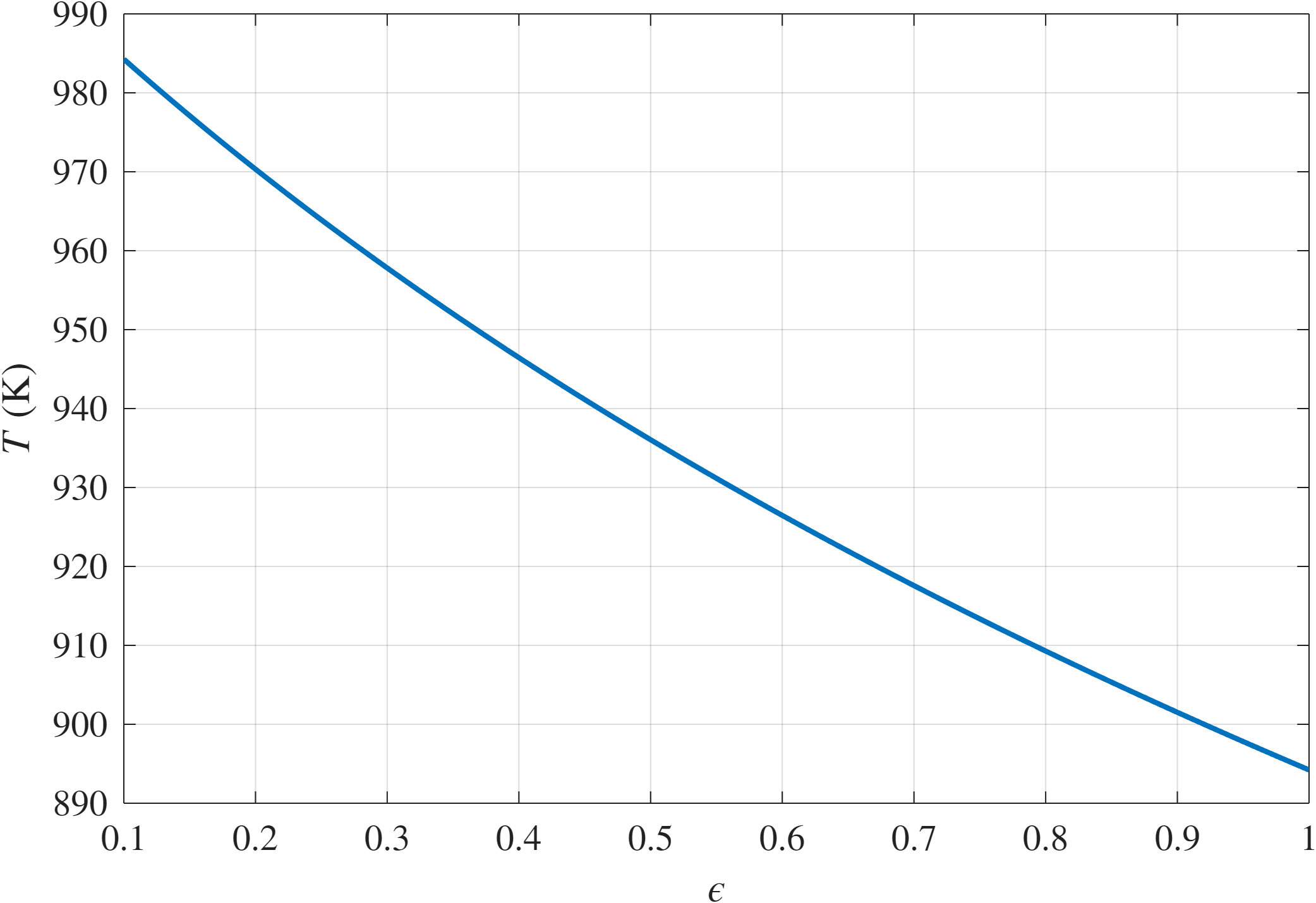
טמפרטורה במצב מתמיד כתלות באמיסיביות.

הקוד נמצא בq4.m.