FLD1_HW003 תרגיל בית 3

	סטודנט א’
שם	עידו פנג בנטוב
ת”ז	322869140
דואר אלקטרוני	ido.fang@campus.technion.ac.il

שאלה 1

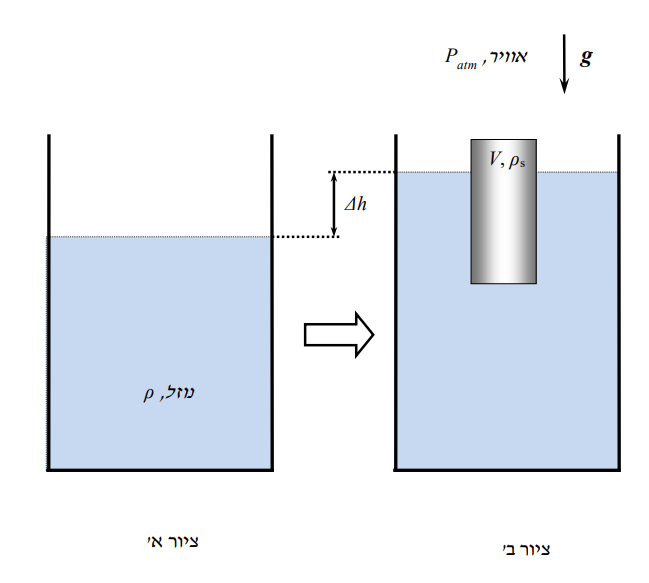
סכימת המיכל

לפי עיקרון ארכימדס:

במקרה שלנו:

נניח וגובה הנוזל בהתחלה הוא , כך שנפחו בהתחלה הוא . לאחר שהוכנס המצוף הגלילי, נפח המצוף השקוע בנוזל והנוזל הוא כעת פשוט , כך שגובהו החדש הוא:

מעצם ההגדרות, . כלומר:

נציב בעיקרון ארכימדס:

שאלה 2

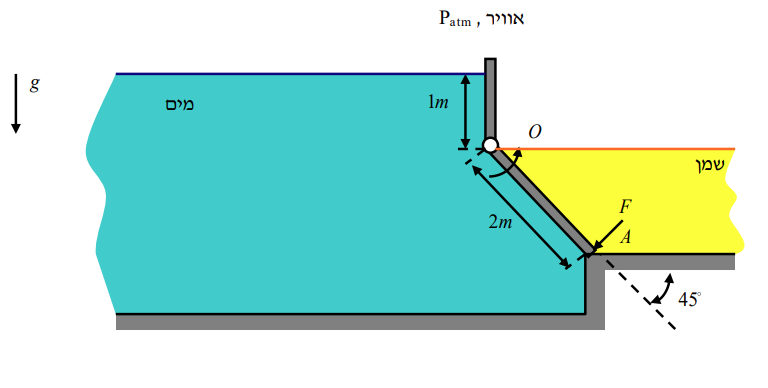
סכימת שני המאגרים

סעיף א’

נרצה שהכוח שאנו מפעילים ייצר מומנט סביב הציר , שיאזן את המומנט סביב אותו הציר שנוצר כתוצאה מהפרשי הלחצים בין המים והשמן.

נתחיל מחישוב המומנט שנוצר כתוצאה מהפרשי הלחצים.

דג”ח על הציר , כאשר רק הפרשי הלחצים פועלים עליו.

נגדיר קואורדינטה , שמתחילה מהציר , ונסכום את המומנט על לפיה (מאוד בדומה ל[[FLD1_HW002 תרגיל בית 2#שאלה 4#סעיף ד’|שאלה בגיליון קודם]]).

כאשר הוא רוחב השער והוא נתון (). נשים לב שגבולות האינטגרציה שלנו הן ו- :

כאשר מוגדר להיות הכיוון בניצב ל-. נשים לב ש- , ולכן:

אכפת לנו רק מהגודל של המומנט (בעיה דו ממדית אין מה לסבך), אז נפשט:

נרצה כעת למצוא את ו-. מאחר והזורמים בשני הצדדים במנוחה, נוכל להשתמש במשוואות ההידרוסטטיקה.

בחירת מערכת הצירים

עבור המים:

התנאי שפה הוא , ולכן:

ולכן:

באותו אופן עבור השמן, נקבל:

נשים לב ש- מקיים:

נסכם ש:

נציב בחזרה בביטוי ל-:

נציב נתונים נקבל:

לפיכך, הכוח , שנמצא במרחק מהציר צריך להיות בגודל:

כדי לאזן את שקול המומנטים בחזרה לאפס.

סעיף ב’

נוכל לרשום את הביטוי ל- כתלות בזווית :

פתיחה חלקית של השער היא הקטנה של , מה שדורש כוח יותר גדול (לפי הביטוי המתמטי). נסיק שהמצב המתואר לא יציב - נדרש להפעיל עוד כוח ככל שפותחים יותר את השער.

שאלה 3

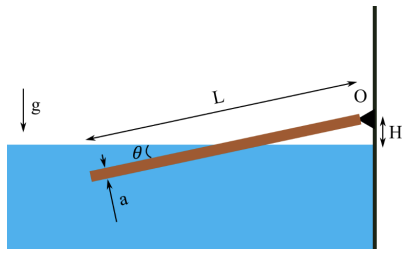
סכימת הקורה

פתרון לא נכון:
לפי עיקרון ארכימדס:

מנתוני השאלה, . נציב:

ואז את נוכל למצוא מגיאומטריה.

הבעיה בפתרון זה הוא שהוא מסתמך על הדג”ח שמופיע בעיקרון ארכימדס. דג”ח זה לא שקול לבעיה שכאן, כי פה עלינו לאזן מומנט סביב ציר מסוים מעל פני המים.

פתרון:

דג”ח על הקורה. הכוח פועל למטה ממרכז הכובד של הקורה. הלחצים פועלים בניצב לגאומטריית הקורה.

נסמן את סך הכוח שהלחץ האטמוספרי מפעיל ב-, וסך הכוח שהלחץ במים מפעיל ב-. נניח גם שמרכז הכוחות האלו פועלים במחצית אורכם בקורה. כלומר, ש- פועל במרחק מ-, ו- פועל במרחק מהקצה.

לכן, שקול המומנטים סביב :

כאשר הוא כיוון הקורה מנקודה .

אנו יודעים גם ש- :

כאשר הוא הכיוון הניצב למישור.
בשיווי משקל, , ולכן:

נשים לב ש- - הלחץ האטמוספירי מאזן אחד את השני משני צדי הקורה, ולכן סך הכוח שהוא מפעיל הוא אפס. בנוסף, נוכל לבטא את כמכפלה של הנפח והצפיפות:

נותר לנו למצוא את ואת הכוח .
עבור , נחשב באותו אופן כמו הפיתוח של עיקרון ארכימדס. הגדרנו כסך הלחץ שמופעל הנפח הטבול:

לפי משפט גאוס:

הנוזל לא בתנועה, ולכן נוכל להשתמש במשוואות ההידרוסטטיקה:

נציב בחזרה ב-:

נחלק את הכל ב-, ונשים לב שגם ו- :

נרצה למצוא את .

ניתוח גיאומטרי של הבעיה

נתחיל מהמשולש הגדול:

בנוסף, מהמשולש הקטן:

נציב את שמצאנו:

נציב ב-:

מבחינת גודל הריאקציה, אם נחזור לדג”ח, אנו כעת יודעים שהכוחות היחידים שפועלים על הקורה הם ו-, פלוס כוח הריאקציה שפועל על הקורה, שלא התייחסנו אליו כי היה אכפת לנו רק מהמומנט סביב . כלומר, משקול כוחות:

נציב את ו-:

נציב את שקיבלנו:

מבחינת כיוונו וגודלו של כוח הריאקציה הפועל על הציר, הוא יהיה פשוט .

שאלה 4

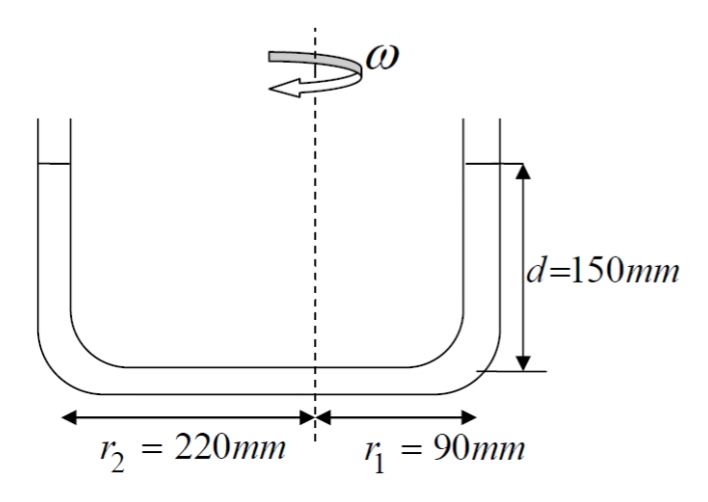
סכימת הצינור

בצורה דומה ל[[FLD1_005 הידרוסטטיקה#שאלה 3#סעיף א’|שאלה בתרגול]], נסיק כי מהידרוסטטיקה ותאוצת המערכת:

נתון כי גובה הזורם במנוחה הוא . כלומר, כאשר , אז בגובה (נגדיר את מערכת הצירים על ציר הסיבוב בתחתית הצינור). לכן:

נציב בחזרה בביטוי ל- ונקבל:

נמצא ביטוי לגובה הנוזל במרחק כללי מהראשית. אנו יודעים שעל שפת הנוזל , ולכן כאשר נציב , נקבל את פרופיל שפת הנוזל:

נרצה שהפרש הגובה בין שתי הזרועות יהיה . כלומר, נדרוש ש:

נציב את הביטוי ל-:

נציב נתונים ונקבל: